For the Love of Physics (7 page)

It happens because of the switch to different lines of sight in observing an object, so in this case from the line of sight of your left eye to that of your right eye (your eyes are about 6.5 centimeters apart).

This is the basic idea behind determining distances to stars. Except that instead of the approximately 6.5 centimeters separation of my eyes as our baseline, we now use the diameter of the Earth’s orbit (about 300 million kilometers) as our baseline. As the Earth moves around the Sun in one year (in an orbit with a diameter of about 300 million kilometers) a nearby star will move in the sky relative to more distant stars. We measure the angle in the sky (called a parallax angle) between the
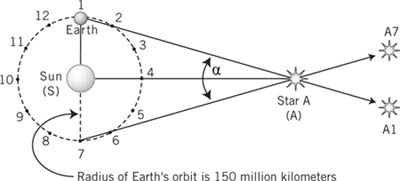
two positions of the star measured six months apart. If you make many sets of measurements all six months apart, you will find different parallax angles. In the figure below, for simplicity, I have selected a star in the same plane of space as Earth, known as the orbital plane (also called the ecliptic plane). However, the principle of parallax measurements as described here holds for any star—not just for stars in the ecliptic plane.

Suppose you observe the star when the Earth is located at position 1 in its orbit around the Sun. You will then see the star projected on the background (very far away) in the direction A1. If now you observe the same star six months later (from position 7), you will see the star in the direction A7. The angle marked as α is the largest possible parallax angle. If you make similar measurements from positions 2 and 8, 3 and 9, 4 and 10, you will then always find parallax angles that are smaller than α. In the hypothetical case of observations from points 4 and 10 (hypothetical, as the star cannot be observed from position 10 since the Sun is then in the way), the parallax angle would even be zero. Now look at the triangle that is formed by the points 1A7. We know that the distance 1–7 is 300 million kilometers, and we know the angle α. Thus we can now calculate the distance
SA
(with high school math).

Even though the parallax angles taken at different six-month intervals vary, astronomers talk about
the
parallax of a star. What they mean by that is half the largest parallax angle. If the maximum parallax angle was 2.00 arc seconds, then
the
parallax would be 1.00 arc seconds and the distance to the star would then be 3.26 light-years (however, there
is no star that close to us). The smaller
the
parallax, the greater the distance. If
the
parallax is 0.10 arc seconds, its distance is 32.6 light-years. The star nearest the Sun is Proxima Centauri. Its parallax is 0.76 arc seconds; thus its distance is about 4.3 light-years.

To understand just how small the changes in stellar positions are that astronomers must measure, we have to understand just how small an arc second is. Picture an enormous circle drawn in the night sky going through the zenith (which is straight overhead) all the way around the Earth. That circle of course contains 360 degrees. Now each degree is divided into 60 arc minutes, and each arc minute is divided in turn into 60 arc seconds. So there are 1,296,000 arc seconds in that full circle. You can see that an arc second is extremely small.

Here’s another way to envision how small. If you take a dime and move it 2.2 miles away from you, its diameter would be one arc second. And here’s another. Every astronomer knows that the Moon is about half a degree across, or 30 arc minutes. This is called the angular size of the Moon. If you could cut the Moon into 1,800 equally thin slices, each one would be an arc second wide.

Since the parallax angles that astronomers must measure in order to determine distances are so very small, you may appreciate how important the degree of uncertainty in the measurements is for them.

As improvements in equipment have allowed astronomers to make more and more accurate measurements, their estimates of stellar distances have changed, sometimes quite dramatically. In the early nineteenth century Thomas Henderson measured the parallax of the brightest star in the heavens, Sirius, to be 0.23 arc seconds, with an uncertainty of about a quarter of an arc second. In other words, he had measured an upper limit for the parallax of about half an arc second, and that meant that the star could not be closer to us than 6.5 light-years. In 1839 this was a very important result. But a half century later, David Gill measured Sirius’s parallax at 0.370 arc seconds with an uncertainty of plus or minus 0.010 arc seconds. Gill’s measurements were consistent with Henderson’s, but Gill’s measurements were highly superior because the uncertainty was twenty-five times smaller. At
a parallax of 0.370 ± 0.010 arc seconds, the distance to Sirius becomes 8.81 ± 0.23 light-years, which is indeed larger than 6.5 light-years!

In the 1990s Hipparcos, the High Precision Parallax Collecting Satellite (I think they fiddled with the name until it matched the name of a famous ancient Greek astronomer), measured the parallaxes of (and hence the distances to) more than a hundred thousand stars with an uncertainty of only about a thousandth of an arc second. Isn’t that incredible? Remember how far away that dime had to be to represent an arc second? To cover a thousandth of an arc second, it would have to be 2,200 miles away from an observer.

One of the stars Hipparcos measured the parallax of was, of course, Sirius, and the result was 0.37921 ± 0.00158 arc seconds. This gives a distance to Sirius of 8.601 ± 0.036 light-years.

By far the most accurate parallax measurement ever made was by radio astronomers during the years 1995 to 1998 for a very very special star called Sco X-1. I will tell you all about it in
chapter 10
. They measured a parallax of 0.00036 ± 0.00004 arc seconds, which translates into a distance of 9.1 ± 0.9 thousand light-years.

In addition to the uncertainties that we must deal with in astronomy as a consequence of the limited accuracy of our equipment, and also to limits in available observation time, there are the astronomers’ nightmares: the “unknown-hidden” uncertainties. Is there perhaps an error you are making that you don’t even know about because you’re missing something, or because your instruments are calibrated incorrectly? Suppose your bathroom scale is set to show zero at 10 pounds and has been that way since you bought it. You only discover the error when you go to the doctor—and nearly have a heart attack. We call that a systematic error, and it scares the hell out of us. I’m no fan of former secretary of defense Donald Rumsfeld, but I did feel a tiny bit of sympathy when he said, in a 2002 press briefing, “We know there are some things we do not know. But there are also unknown unknowns—the ones we don’t know we don’t know.”

The challenges of the limits of our equipment make the achievement of one brilliant but mostly ignored female astronomer, Henrietta Swan
Leavitt, all the more astonishing. Leavitt was working at the Harvard Observatory in a low-level staff position in 1908 when she started this work, which enabled a giant jump in measuring the distance to stars.

This kind of thing has happened so often in the history of science that it should be considered a systematic error: discounting the talent, intellect, and contributions of female scientists.
*

Leavitt noticed, in the course of her job analyzing thousands of photographic plates of the Small Magellanic Cloud (SMC), that with a certain class of large pulsating stars (now known as Cepheid variables), there was a relationship between the star’s optical brightness and the time it took for one complete pulsation, known as the star’s period. She found that the longer the period, the brighter the star. As we will see, this discovery opened the door to accurately measuring distances to star clusters and galaxies.

To appreciate the discovery, we first must understand the difference between brightness and luminosity. Optical brightness is the amount of energy per square meter per second of light we receive on Earth. This is measured using optical telescopes. Optical luminosity, on the other hand, is the amount of energy per second radiated by an astronomical object.

Take Venus, often the brightest object in the entire night sky, even brighter than Sirius, which is the brightest star in the sky. Venus is very close to Earth; it’s therefore very bright, but it has virtually no intrinsic luminosity. It radiates relatively little energy by comparison to Sirius, a powerful, nuclear-burning furnace twice as massive as our Sun and about twenty-five times as luminous. Knowing an object’s luminosity tells astronomers a great deal about it, but the tricky thing about luminosity was that there was no good way to measure it. Brightness is what you measure because it’s what you can see; you can’t measure luminosity. To measure luminosity you have to know both the star’s brightness and its distance.

Using a technique called statistical parallax, Ejnar Hertzsprung, in 1913, and Harlow Shapley, in 1918, were able to convert Leavitt’s brightness values into luminosities. And by assuming that the luminosity of a Cepheid with a given period in the SMC was the same as that of a Cepheid with the same period elsewhere, they had a way to calculate the luminosity relationship for all Cepheids (even those outside the SMC). I won’t elaborate here on this method, as it gets quite technical; the important thing to appreciate is that working out the luminosity-period relation was a milestone in measurements of distances. Once you know a star’s luminosity and its brightness, you can calculate its distance.

The range in luminosity, by the way, is substantial. A Cepheid with a period of three days has about a thousand times the Sun’s luminosity. When its period is thirty days, its luminosity is about thirteen thousand times greater than the Sun’s.

In 1923, the great astronomer Edwin Hubble found Cepheids in the Andromeda Galaxy (also known as M31), from which he calculated its distance at about 1 million light-years, a genuinely shocking result to many astronomers. Many, including Shapley, had argued that our own Milky Way contained the entire universe, including M31, and Hubble demonstrated that in fact it was almost unimaginably distant from us. But wait—if you google the distance to the Andromeda Galaxy, you’ll find that it’s 2.5 million light-years.

This was a case of unknown unknowns. For all his genius, Hubble had made a systematic error. He had based his calculations on the known luminosity of what later came to be known as Type II Cepheids, when in fact he was observing a kind of Cepheid variable about
four times
more luminous than what he thought he was seeing (these were later named Type I Cepheids). Astronomers only discovered the difference in the 1950s, and overnight they realized that their distance measurements for the previous thirty years were off by a factor of two—a large systematic error that
doubled
the size of the known universe.

In 2004, still using the Cepheid variable method, astronomers measured the distance to the Andromeda Galaxy at 2.51 ± 0.13 million lightyears.
In 2005 another group measured it by using the eclipsing binary stars method, to get a result of 2.52 ± 0.14 million light-years, about 15 million trillion miles. These two measurements are in excellent agreement with each other. Yet the uncertainty is about 140,000 light-years (about 8 × 10
¹⁷
miles). And this galaxy is by astronomical standards our next-door neighbor. Imagine the uncertainty we have about the distances of so many other galaxies.

You can see why astronomers are always on the hunt for what are called standard candles—objects with known luminosities. They allow us to estimate distances using a range of ingenious ways of establishing reliable tape measures to the cosmos. And they have been vital in establishing what we call the cosmic distance ladder.

We use parallax to measure distances on the first rung on that ladder. Thanks to Hipparcos’s fantastically accurate parallax measurements, we can measure the distances of objects up to several thousand light-years with great precision this way. We take the next step with Cepheids, which allow us to obtain good estimates of the distances of objects up to a hundred million light-years away. For the next rungs astronomers use a number of exotic and complicated methods too technical to go into here, many of which depend on standard candles.

The distance measurements become more and more tricky the farther out we want to measure. This is partly due to the remarkable discovery in 1925 by Edwin Hubble that all galaxies in the universe are moving away from one another. Hubble’s discovery, one of the most shocking and significant in all of astronomy, perhaps in all of science in the past century, may only be rivaled by Darwin’s discovery of evolution through natural selection.

Hubble saw that the light emitted by galaxies showed a distinct shift toward the less energetic end of the spectrum, the “red” end where wavelengths are longer. This is called redshift. The larger the redshift, the faster a galaxy is moving away from us. We know this effect on Earth with sound as the Doppler effect; it explains why we can tell whether an ambulance is coming toward us or going away from us, since the notes
are lower when it’s speeding away and higher as it speeds toward us. (I will discuss the Doppler shift in more detail in
chapter 13
.)