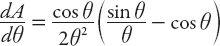X and the City: Modeling Aspects of Urban Life (75 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

Figure 25.2. Circular wave pattern II—caused by raindrops?
Answer:
The one in
Figure 25.1
. Raindrops falling on the surface of a puddle generate wave patterns that are dominated by the effects of surface tension. The speed of these waves is
inversely
proportional to the square root of the wavelength; thus
shorter
waves travel faster and move out first. Note the expanding region of calm associated with and inside these waves. The other pattern is dominated by gravity, which produces longer waves with speeds
directly
proportional to the square root of the wavelength, so the
longer
waves travel faster and move out first.

Figure 25.3. This rather pedestrian photograph (!) was taken from a sheltered area outside the Mt. Washington Resort, Bretton Woods, New Hampshire, on September 30, 2010, courtesy of Tropical Storm Nicole. Because of the heavy rain, Mt. Washington was nowhere to be seen! Nevertheless, it seemed like fun to “guesstimate” the speed of the raindrops, given that the exposure time for the shot was 1/200 second and using an estimate for the width of my sneaker (you don’t need to know my shoe size to do this.). My foot and the raindrops shown were about the same distance from the camera. You can assume that the foreshortening of the rain streaks (due to the downward angle of the camera) is not significant.
Once home, you upload your pictures onto the computer. On noticing the picture you took back at the shelter, you realize that knowing the exposure time of the shot, you can estimate the speed of the rain. The picture is given in
Figure 25.3
; can you find the speed of the rain?
Solution
: From the photograph,. The width of my sneaker is approximately 5 inches, so the raindrops traveled approximately 5/3 inches in 1/200th of a second, or 1000/3 inches/s, or 1000/36 ft/s. Therefore
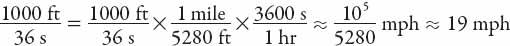
Since 1 m/s ≈ 2.2 mph, this is about 8.6 m/s.
For those who don’t have access to my foot, anything in the range 4 inches to 6 inches wide is a reasonable estimate. This would result in a range of speeds 15–23 mph (7–10 m/s).
THEOREMS FOR PRINCESS DIDO
Being a princess isn’t all it’s cracked up to be.
—Princess Diana
We shall state two theorems that undergird Princess Dido’s “solution” discussed in
Chapter 1
: (i) the isoperimetric property of the circle (without proof), and (ii) the “same area” theorem (with proof). The word
isoperimetric
means “constant perimeter,” and here concerns the largest area that can be enclosed by a closed curve of constant length. We shall be a little more formal in our language for the statement of these results.
Theorem 1 (the isoperimetric theorem):
Among all planar figures of equal perimeter, the circle (and only the circle) has maximum area.
There is also an equivalent “dual” statement:
Theorem 2 (the same area theorem):
Among all planar figures of equal area, the circle (and only the circle) has minimum perimeter.
This theorem is a consequence of Theorem 1, as we can show. Consider first a closed curve
C
of perimeter
L
enclosing a domain of area
A
. Let
r
be the radius of a circle of perimeter
L
: then
L
= 2
πr
. This encloses a disk of area
πr
2
. By the isoperimetric property of the circle, the area enclosed by
C
cannot exceed
πr
2
, and it equals
πr
2
if and only if
C
is a circle. On the other hand,
πr
2
=
L
2
/4
π
, so we obtain the
isoperimetric inequality A
≤
L
2
/4
π
, with the equality holding
only
for a circle. Now we are ready for the proof of Theorem 2 assuming the isoperimetric theorem. Consider next an arbitrary planar figure
with perimeter
L
and area
A
. Let
D
be a circular disk with the same area
A
and perimeter
l
: then
A
=
l
2
/4
π
. If
l
>
L
, the isoperimetric inequality would be violated, so
L
≥
l
.
To complete the argument for Princess Dido and the semicircular area discussed in
Chapter 1
, we can examine a generalization of this problem. Suppose that a curve of length
L
is now attached to a line segment of fixed length
l
, forming a closed curve. What should be the shape of
L
in order for the area enclosed to be a maximum? Consider two situations, the first in which
L
is a circular arc (enclosing an area
A
c
), and the second in which it is not (and enclosing an area
A
). Imagine also that in both cases a circular arc below the line segment
l
is added to give an additional segment of area
a
. By the isoperimetric theorem,
A
+
a
≤
A
c
+
a
, so that
A
≤
A
c
; clearly Princess Dido knew what she was doing!
PRINCESS DIDO AND THE SINC FUNCTION
We’ll make an alliterative foray further into this forest by generalizing Dido’s “classical” Carthage problem somewhat. Recall that she formed a semicircular arc, with the (presumed) straight Mediterranean coastline as a diameter, thus enclosing a semicircular area for the city.
Clearly, the strip length
L
was shorter than the Mediterranean coastline, but what about the case where the available straight boundary is of
variable
length
l
<
L
; how does the area of the closed region vary with
l
? In fact, how do we know now that the semicircular area is still a maximum? We’ll do a little more mathematics and put in some numerical values just for fun, and work with
l
expressed in units of
L
, so that 0 <
l
< 1. Note that if
l
= 1 the enclosed area
A
is zero; the strip
L
= 1 is collinear with
l
, and if
l
= 0 the area of the circle is just 1/4
π
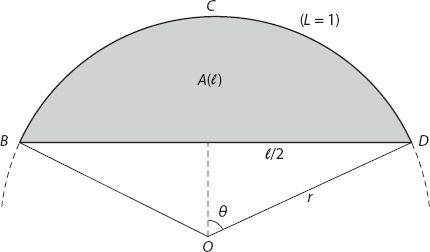
square units, half that of the area enclosed by the boundary and the completing semicircular arc. To investigate this, examine the circular segment
BCD
in
Figure A2.1
. The shaded area
A
(
l
) is enclosed by the circular arc of fixed unit length and the line segment of length
l
.
The arc subtends an angle 2
θ
at the center O, 0 <
θ
≤
π
. The arc length 2
rθ
= 1. In terms of
θ
the area of the shaded segment is
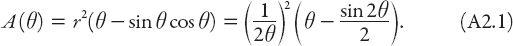
Note that, for
π
/2 <
θ
≤
π
this formula is still correct, but now cos
θ
< 0. A graph of
A
(
θ
) is shown below (
Figure A2.2
). It does indeed appear that the maximum enclosed area occurs when the region is a semicircle (
θ
=
π
/2). This is easily verified by noting that