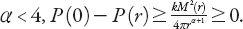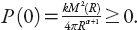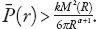X and the City: Modeling Aspects of Urban Life (49 page)

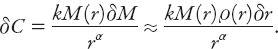
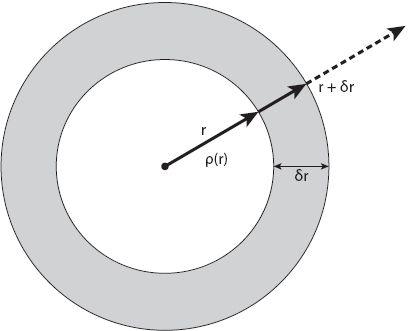
Figure 17.1. Schematic geometry for the civic mass integral in equation (17.1).

In this equation, the “civic coercion” constant
k
and
α
are also positive constants; for strictly two-dimensional “gravitational attraction”
α
= 1, but we shall keep it arbitrary for most of this chapter. Assuming further that
C
(
r
) is differentiable, we find that, using the standard limiting procedure, that

The civic pressure gradient is from the higher housing-cost pressures in the central city regions to the lower pressure regions farther out. The cohesive pressure is higher in these external regions, and so the corresponding pressure gradient is in the opposite direction. For a city in equilibrium, therefore, the following equation must be satisfied:

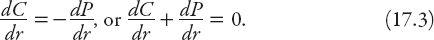
From equations (17.2) and (17.3) we find that

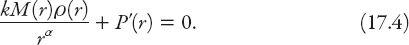
There are several general properties of our “city” that can be established from this equilibrium equation. For example, it follows trivially that the rental gradient
P
′(
r
) vanishes at any noncentral location where the population density
ρ
(
r
) = 0. In particular, the following exercise is left to the reader:

Exercise:
Prove the following results:

(a) The central rental gradient
P
′(0) is always zero at an equilibrium provided
α
< 2. (Hint: use L’Hôpital’s rule.)

(b) The quantity
decreases monotonically outward for
r
> 0.

(c) For all
r
, and

(d) If the rental
P
(
r
) = 0 for some radius
r
=
R
, then the central rental
P
(0) satisfies

Further results can be found by using the following definition of a mean rental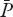
(
r
):

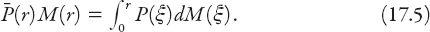
Exercise:
Prove that if the central rental
P
(0) ≥ 0, then
and hence that