Why Beauty is Truth (35 page)

The reaction to Hamilton's solution of a three-hundred-year-old conundrum was distinctly muted. Once mathematicians had woven the notion of complex numbers into a powerful coherent theory, fears about the existence of complex numbers became unimportant. But Hamilton's use of pairs turned out nonetheless to be very significant. Even though the issue of complex numbers was no longer a source of excitement, the idea of building new number systems from old ones took root in the mathematical consciousness.

Complex numbers, it turned out, were useful not only in algebra and basic calculus. They constituted a powerful method for solving problems about fluid flow, heat, gravity, sound, almost every area of mathematical physics. But they had one major limitation: they solved these problems in two-dimensional space, not the three that we live in. Some problems, such as the motion of the skin of a drum or the flow of a thin layer of fluid,
can be reduced to two dimensions, so the news isn't all bad. But mathematicians became increasingly irritated that their complex-number methods could not be extended from a plane to space of three dimensions.

Might there be an undiscovered extension of the number system to three dimensions? Hamilton's formalization of complex numbers as
pairs
of real numbers suggested a way to approach this proposal: try to set up a number system based on
triples
(
x, y, z
). The problem was that no one had worked out an algebra of triples. Hamilton decided to try.

Adding triples was easy: you could take a hint from complex numbers and just add corresponding coordinates. This kind of arithmetic, known today as “vector addition,” obeys very pleasant rules, and there is only one sensible way to do it.

The bugbear was multiplication. Even for the complex numbers, multiplication does not work like addition. You do not multiply two pairs of real numbers by separately multiplying their first and second components. If you do, a lot of pleasant things happen—but two fatally unpleasant ones happen as well.

The first is that there is no longer a square root of minus one.

The second is that you can multiply two nonzero numbers together and get zero. Such “divisors of zero” play merry hell with all of the usual algebraic methods, such as ways to solve equations.

For the complex numbers we can overcome this obstacle by choosing a less obvious rule for multiplication, which is what Hamilton did. But when he tried similar tricks on triples of numbers, he got a horrible shock. Try as he might, he could not avoid some fatal defect. He could get a square root for minus one, but only by introducing divisors of zero. Getting rid of divisors of zero seemed to be completely impossible, whatever else he did.

If you're thinking that this sounds a bit like attempts to solve the quintic, you're onto something. If many capable mathematicians try something and fail, it is conceivable that it may be impossible. If there is one big thing mathematics has taught us, it is that many problems do not have solutions. You can't find a fraction whose square is 2. You can't trisect an angle with straightedge and compass. You can't solve the quintic by radicals. Mathematics has limits. Maybe you can't construct a three-dimensional algebra with all the nice properties you would like it to have.

If you're serious about finding out whether that is indeed the case, a program of research opens up. First you need to specify the properties you want your three-dimensional algebra to have. Then you must analyze the consequences of those properties. Given enough information from that program, you can search for features that such an algebra must have if it does exist, and reasons why it might not exist.

At least, that's what you would do today. Hamilton's approach was not so systematic. He tacitly assumed that his algebra must have “all” reasonable properties, and suddenly realized that one of them might have to be dispensed with. More significantly, he realized that an algebra of three dimensions was not in the cards. The closest he could get was four. Quadruples, not triples.

Back to those elusive rules of algebra. When mathematicians do algebraic calculations, they rearrange symbols in systematic ways. Recall that the original Arabic name “al-jabr” means “restoration”—what nowadays we call “move the term to the other side of the equation and change its sign.” Only within the last 150 years have mathematicians bothered to make explicit lists of the rules behind such manipulations, deriving other well-known rules as logical consequences. This axiomatic approach does for algebra what Euclid did for geometry, and it took mathematicians only two thousand years to get the idea.

To set the scene, we can focus on three of these rules, all related to multiplication. (Addition is similar but more straightforward; multiplication is where everything starts to go pear-shaped.) Children learning their multiplication tables eventually notice some duplication of effort. Not only does three times four make twelve: so does four times three. If you multiply two numbers together you get the same result whichever one comes first. This fact is called the
commutative law
, and in symbols it tells us that
ab
=
ba
for any numbers
a
and
b.
This rule also holds in the extended system of complex numbers. You can prove this by examining Hamilton's formulas for how to multiply pairs.

A subtler law is the
associative law
, which says that when you multiply three numbers together in the same order, it makes no difference where you start. For example, suppose I want to work out 2 × 3 × 5. I can start with 2 × 3, getting 6, and then multiply 6 by 5. Alternatively, I can start with 3 × 5, which is 15, and then multiply 2 by 15. Either method yields the same result, namely 30. The associative law states that this is always the case; in symbols it says that (
ab
)
c
=
a
(
bc
), where the parentheses show the
two ways to do the multiplication. Again, this rule holds for both real and complex numbers, and this can be proved using Hamilton's formulas.

A final, very useful rule—let me call it the
division law
, although you will find it in the textbooks as “existence of a multiplicative inverse”—states that you can always
divide
any number whatsoever by any nonzero number. There are good reasons to forbid division by zero: the main one is that it seldom makes sense.

We saw earlier that you can manufacture an algebra of triples using an “obvious” form of multiplication. This system satisfies the commutative law and the associative law. But it fails to obey the division law.

Hamilton's great inspiration, reached after hours of fruitless searching and calculation, was this: it is possible to form a new number system in which both the associative law and the division law are valid, but you have to sacrifice the commutative law. Even then, you can't do it with triples of real numbers. You have to use quadruples. There is no “sensible” three-dimensional algebra, but there is a fairly nice
four
-dimensional one. It is the only one of its kind, and it falls short of the ideal in just one respect: the commutative law fails.

Does that matter? Hamilton's biggest mental block was in thinking that the commutative law was essential. All that changed in an instant when, inspired by who knows what, he suddenly understood how to multiply quadruples. The date was 16 October 1843. Hamilton and his wife were walking along the towpath of the Royal Canal, heading for a meeting of the prestigious Royal Irish Academy in Dublin. His subconscious mind must have been churning away at the problem of three-dimensional algebra, because inspiration suddenly struck. “I then and there felt the galvanic circuit of thought
close
,” he wrote in a subsequent letter, “and the sparks which fell from it were the
fundamental equations between i
,
j
,
k; exactly such
as I have used them ever since.”

So overcome was Hamilton that he immediately carved the formulas into the stonework of Broome Bridge (he called it “Brougham”). The bridge survives, but not the carving—though there is a commemorative plaque. The formulas also survive:

i
²
=
j
²
=
k
²
=
ijk
= –1

These are very pretty formulas, with a lot of symmetry. But what you are probably wondering is, where are the quadruples?

Complex numbers can be written as pairs (
x, y
), but they are usually written as
x
+
iy
where
i
=
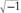. In the same manner, the numbers Hamilton had in mind could be written either as quadruples (
x, y, z, w
) or as a combination
x
+
iy
+
jz
+
kw.
Hamilton's formulas use the second notation; if you are of a formal turn of mind, you may prefer to use quadruples instead.

Hamilton called his new numbers
quaternions.
He proved that they obey the associative law and—remarkably, as it later transpired—the division law. But not the commutative law. The rules for multiplying quaternions imply that
ij
=
k
, but
ji
= –
k
.

The system of quaternions contains a copy of the complex numbers, the quaternions of the form
x
+
iy.
Hamilton's formulas show that –1 does not have just two square roots,
i
and –
i
. It also has
j
, –
j
,
k
, and –
k
. In fact there are infinitely many different square roots of minus one in the quaternion system.

So along with the commutative law, we have also lost the rule that a quadratic equation has two solutions. Fortunately, by the time quaternions were invented, the focus of algebra had shifted away from the solution of equations. The advantages of quaternions greatly outweighed their defects. You just had to get used to them.

In 1845, Thomas Disney visited Hamilton and brought his daughter, William's childhood love Catherine, with him. By then she had lost her first husband and married again. The encounter reopened old wounds, and Hamilton's reliance on alcohol became more severe. He made such a complete fool of himself at a scientific dinner in Dublin that he went on the wagon and drank only water for the next two years. But when the astronomer George Airy began taunting him for his abstinence, Hamilton responded by downing alcohol in large quantities. From then on he was a chronic alcoholic.

Two uncles died, and a friend and colleague committed suicide; then Catherine started writing to him, which made his depression worse. She quickly realized that what she was doing was not proper for a respectable married woman, and made a half-hearted attempt to kill herself. She separated from her husband and went to live with her mother.