The Numbers Behind NUMB3RS (9 page)

No arrests were made on that occasion. But the authorities did obtain a good picture of the conference call pattern associated with that kind of activity, and it is possible that, based on the findings of the study, the telephone company subsequently trained one of its own neural networks to look for similar patterns
as they occur
, to try to catch the perpetrators in the act. (This is the kind of thing that companies tend to keep secret, of course.)

Battles such as this never end. People with criminal intent will continue to look for ways to defraud the telecommunications companies. Data mining is the principal weapon the companies have in their arsenal to keep abreast of their adversaries.

MORE DATA MINING IN
NUMB3RS

Given the widespread use of data-mining techniques in many areas of modern life, including crime detection and prevention, it is hardly surprising that Charlie mentions it in many episodes of
NUMB3RS
. For example, in the episode “Convergence,” broadcast on November 11, 2005, a chain of robberies at upscale Los Angeles homes takes a more sinister turn when one of the homeowners is murdered. The robbers seem to have a considerable amount of inside information about the valuable items in the houses they rob and the detailed movements of the homeowners. Yet the target homes seem to have nothing in common, and certainly nothing that points to a source for the information the crooks are clearly getting. Charlie uses a data-mining program he wrote to look for patterns among all robberies in the area over the six-month period of the home burglaries, and eventually comes up with a series of car thefts that look as though they could be the work of the same gang, which leads to their capture.

Further Reading

Colleen McCue,
Data Mining and Predictive Analysis
, Butterworth-Heinemann (2007).

Jesus Mena,
Investigative Data Mining for Security and Criminal Detection
, Butterworth-Heinemann (2003).

Changepoint Detection

THE BASEBALL NUMBERS GENIUS

In a third-season
NUMB3RS
episode entitled “Hardball,” an aging baseball player, trying to make a comeback after several lackluster years in the minors, dies during on-field training. When the coach opens the dead player's locker, he finds a stash of needles and vials of steroids, and at once contacts the police. The coroner's investigation shows that the player suffered a brain hemorrhage resulting from a massive overdose of steroids, which he had started using to enhance his prospects of a return to the major league. But this was no accidental overdose. The drug in his locker was thirty times more powerful than the normal dosage, and had to have been prepared specially. The player had been murdered.

When Don is assigned to the case, he discovers some e-mails on the player's laptop from an unknown person who claimed to know that he was taking performance-enhancing drugs and threatened to inform the authorities. It looks like a case of blackmail. What is unusual is the proof that the unknown extortionist claimed to have. The e-mails have an attachment—a page of mathematical formulas that, the e-mailer claimed, showed exactly when in his professional career the player had started taking steroids.

Clearly, this was another case where Don would need the help of his younger brother. Charlie recognizes at once what the mathematics is about. “That's advanced statistical baseball analysis,” he blurts out.

“Right, sabermetrics,” replies Don, giving the accepted technical term for the use of statistics to analyze baseball performance.

The term “sabermetrics” is derived from the acronym SABR, which stands for the Society for American Baseball Research, and was coined by baseball statistics pioneer Bill James, one of the most enthusiastic proponents of using numbers to analyze the game.

Charlie also observes that whoever produced the formulas had devised his own mathematical abbreviations, something that might help identify him. Unfortunately, he does not know enough about the sabermetrics community to have any idea who might be behind the e-mail. But a colleague at CalSci has no trouble providing Charlie with the missing information. A quick search of several websites devoted to fantasy baseball soon reveals postings from an individual using the same mathematical notation.

For Don, the picture is now starting to emerge. The dead player had been killed to keep him from talking about the ring that was supplying him—and very likely other athletes—with illegal drugs. Obviously, the e-mails from the anonymous sabermetrician were what caused the fear that the narcotics ring would be discovered. But who was the killer: the e-mailer, the drug supplier, or someone else?

It does not take Don very long to trace the e-mail to a nerdy, twenty-five-year-old, high school dropout named Oswald Kittner, who used his self-taught mathematical abilities to make a fairly good living winning money by playing fantasy-league baseball. In this virtual arena, players create hypothetical teams of real players, which play against each other as computer simulations based on the current statistics for the real players. Kittner's success was based on his mathematical formulas, which turned out to be extremely good at identifying sudden changes in a player's performance—what is known in statistical circles as “changepoint detection.”

As Charlie notes, what makes baseball particularly amenable to statistical analysis is the wealth of data it generates about individual performances coupled with the role of chance—e.g., the highly random result that comes with each pitch.

But Kittner had discovered that his math could do something else besides helping him to make a good living winning fantasy-league games. It could detect when a player started to use performance enhancing drugs. Through careful study of the performance and behavior of known steroid users in baseball, Kittner had determined the best stats to look for as an indication of steroid use—measuring long-ball hitting, aggressive play (being hit by pitches, for example), and even temper tantrums (arguments, ejections from games, and so forth). He had then created a mathematical surveillance system to monitor the best stats for all the players he was interested in, so that if any of them started using steroids, he would detect the changes in their stats and be able to react quickly. This would give him reliable information that a particular player is using steroids long before it becomes common knowledge.

“This is amazing,” Charlie says as he looks again at the math. “This Kittner person has reinvented the Shiryayev–Roberts changepoint detection procedure!”

But was Kittner using his method to blackmail players or simply to win fantasy-league games by knowing in advance that a key player's performance was about to improve dramatically? Either way, before the young fan could put his new plan into action, one of his targets was murdered. And now the nerdy math whiz finds himself a murder suspect.

Kittner quickly comes clean and starts to cooperate with the authorities, and it does not take Don very long to solve the case.

CHANGEPOINT DETECTION

When it comes to crime, prevention is always better than trying to catch the perpetrators after the event. In some cases, the benefit of prevention can be much higher. For terrorist acts, such as those of September 11, 2001, the only way to preempt the attack is by getting information about the plotters before they can strike. This is what happened in the summer of 2006, when British authorities prevented a multiple attack on transatlantic planes using liquid explosives brought on board disguised as soft drinks and toiletries. A bioterrorist attack, on the other hand, may take weeks or months to reach full effect, as the pathogen works its way through the population. If the authorities can detect the pathogen in the relatively early stages of its dispersal, before its effect reaches epidemic proportions, it may be possible to contain it.

To this end, various agencies have instigated what is known as
syndromic surveillance
, where lists of pre-identified sets of symptoms are circulated among hospital emergency room personnel and certain other medical care providers, who must report to public health agencies if these symptoms are observed. Those agencies monitor such data continuously and use statistical analysis to determine when the frequency of certain sets of symptoms is sufficiently greater than normal to take certain predefined actions, including raising an alarm. Among the best-known systems currently in operation are RODS (Realtime Outbreak and Disease Surveillance) in Pennsylvania, ESSENCE (Early Notification of Community-Based Epidemics) in Washington, D.C., and the BioSense system implemented by the Centers for Disease Control and Prevention.

The principal challenge facing the designer of such a monitoring system is to identify when an activity pattern—say, a sudden increase in people taking time off from work because of sickness, or people visiting their doctor who display certain symptoms—indicates something unusual, above and beyond the normal ebb and flow of such activities. Statisticians refer to this task as
changepoint detection
—the determination that a definite change has occurred, as opposed to normal fluctuations.

In addition to syndromic surveillance—quickening the response to potential bioterrorist attacks by continuously collecting medical data, such as symptoms of patients showing up in emergency rooms—mathematical algorithms for changepoint detection are used to pinpoint other kinds of criminal and terrorist activity, such as

• Monitoring reports to detect increases in rates of certain crimes in certain areas
  
• Looking for changes in the pattern of financial transactions that could signal criminal activity
  

OUT OF INDUSTRY

The first significant use of changepoint detection systems was not for fighting crime, however, but for improving the quality of manufactured goods. In 1931, Walter A. Shewhart published a book explaining how to monitor manufacturing processes by keeping track of data in a control chart.

Shewhart, born in New Canton, Illinois, in 1891, studied physics at the Universities of Illinois and California, eventually earning a Ph.D., and was a university professor for a few years before going to work for the Western Electric Company, which made equipment for Bell Telephone. In the early days of telephones, equipment failure was a major problem, and everyone recognized that the key to success was to improve the manufacturing process. What Shewhart did was show how an ingenious use of statistics could help solve the problem.

His idea was to monitor an activity, such as a production line, and look for a change. The tricky part was to decide whether an unusual reading was just an anomaly—one of the random fluctuations that the world frequently throws our way—or else a sign that something had changed (a changepoint). (See figure 4.)

Clearly, you have to look at some additional readings before you can know. But how many more readings? And how certain can you be that there really has been a change, and not just an unfortunate, but ultimately insignificant, run of unexpected readings? There is a trade-off to be made here. The more additional readings you take, the more confident you can be that there has been a change, but the longer you will have to wait before you can take action. Shewhart suggested a simple method that worked: You simply wait until you see an unusual result that is statistically well off the average, say three standard deviations. This method was a huge improvement, but it could still take a long time before a change was detected—too long for many applications, particularly those involved in crime detection and terrorism prevention. The key to a real advance was to use mathematics.

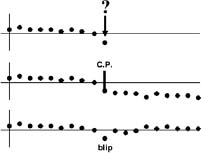
Figure 4. Is an anomalous data point just a blip or a sign of a change?

MATHEMATICS GETS INTO THE ACT

Around twenty-five years after Shewhart's book appeared, mathematicians in England (E. S. Page), the Soviet Union (A. N. Shiryayev), and the United States (S. W. Roberts) found several much more efficient (and mathematically sophisticated) ways to detect changepoints.

As the mathematical theory blossomed, so did the realization in industry and various branches of government (including law enforcement) that changepoint detection methods can be applied to a wide range of real-world problems. Such methods are now known to be useful in applications limited not only to industrial quality control but to such areas as:

• medical monitoring
  
• military applications (e.g., monitoring communication channels)
  
• environmental protection
  
• electronic surveillance systems
  
• surveillance of suspected criminal activity
  
• public health monitoring (e.g., bioterrorism defense)
  
• counterterrorism
  

To show how a more efficient changepoint detection method works, we'll focus on Page's procedure. (The Shiryayev–Roberts method that Charlie Eppes mentions is slightly more technical to describe.) We'll look at an easier example than quality control: namely, detecting an increase in the frequency of some event.

Suppose that over some substantial period of time, it has been observed that a particular event occurs about once a month. Put another way, the probability of it happening on any given day is about 1 out of 30. Examples abound—a New Yorker finds a parking space on the street in front of her apartment, a husband actually
offers
to take out the garbage, a local TV news show doesn't lead off with a natural disaster or violent crime, and so on.

Now suppose that the frequency of a given event could increase dramatically—to once a week, say. We want to set up a changepoint detection system to react as quickly as possible without raising a false alarm too frequently.

The key issue we have to deal with is that chance fluctuations such as 3 or 4 occurrences in a single month can appear to indicate that the frequency has changed from once every 30 days to once every 7 days, even when there has not really been a change.

In the Page procedure, we introduce a numerical index, S, that tracks the activity. S is set initially equal to 1, and you revise S each day, using certain probability calculations, as we shall see shortly. When the value of S reaches or exceeds a certain pre-assigned level (we'll take 50 for the value in our example), you declare that a change has occurred. (Note that it is
not
required to estimate exactly
when
the change occurred, only to determine whether or not it
has
occurred.)

How do you “update” S each day? You multiply S by the probability of whatever happened that day,
assuming a change has already occurred
, and dividing it by the probability of whatever happened,
assuming a change has not occurred
.