The Flamingo’s Smile (19 page)
Read The Flamingo’s Smile Online
Authors: Stephen Jay Gould

REPRINTED FROM NATURAL HISTORY
.
If once the genera of Minerals, Plants and Animals come to stand correctly opposite each other, a great advantage will accrue therefrom to the science of Materia Medica; for corresponding genera will act specifically upon each other.
I admire the sweep and coherence of Oken’s vision, but I’ll descend to the realm of sound and be a monkey’s uncle if it says anything much about nature.
As Oken constructed his ascending wheels of five in Germany during the decades before Darwin, another taxonomic theory, the quinary system, led many English naturalists to arrange all organisms into different circles of five. The quinary system invites comparison with Oken’s scheme because it also built circles of five at different scales and sought correspondences between organisms at the same position on different circles. It also attempted to resolve the apparent contradiction between linear progress and circular repetition.
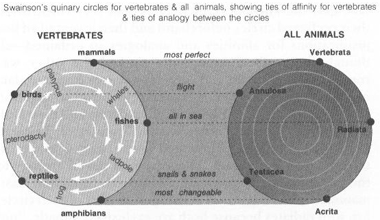
The quinary system rests upon a separation between two kinds of similarity: affinity and analogy. Ties of affinity unite forms on the same circle; analogies specify correspondence between circles. For example, William Swainson, a leading British quinarian, justified the following circle of vertebrates in 1835. We recognize fish, amphibians, reptiles, birds, and mammals as five groups of common anatomical design. But how can they represent both an ascending pathway and a closed circle of five? Swainson argues that we must unite each pair by an intermediate form showing ties of affinity—fish to amphibian by the tadpole, amphibian to reptile by the adult frog, reptile to bird by the flying pterodactyl, bird to mammal by the duck-billed platypus, and mammal back to fish by the largest agent of natural transport, whales. Since whales connect the highest mammals to the lowest fish, the path of progress curves back on itself and forms a circle. “Nature herself,” Swainson proclaimed, “describes the mighty circle and pronounces it complete.”
REPRINTED FROM NATURAL HISTORY
.
The circle of vertebrates can then be united with other circles at both smaller and larger scales by ties of analogy linking groups in similar positions. (I must confess that Swainson’s arguments seem as forced as Oken’s. The quinarians never presented rigorous criteria for why certain relationships should be called affinity and others analogy. One gets the uncomfortable feeling that they constructed their preferred circles beforehand and then invented ad hoc justifications for affinities and analogies so ordained—although the method supposedly worked the other way round, building circles and correspondences from raw data of affinity and analogy.) For example, Swainson arranged all animals into a circle of Radiata (echinoderms and their kin), Acrita (protozoans and other “simple” creatures), Testacea (mollusks), Annulosa (segmented worms, insects, and crustaceans), and Vertebrata. The supposed ties of analogy to the vertebrate circle seem a bit contrived, to say the least: mammals with vertebrates as the most perfect of each circle; fish with radiates because both are exclusively aquatic, “not one species in either group having yet been discovered upon the land” Amphibia with Acrita because both (get this) “however dissimilar in other respects are remarkable for changing their shapes more than any other of the aberrant types in either circle” reptiles with mollusks because both serpents and snails lack feet and crawl on their bellies; and birds with Annulosa because insects fly too.
I was disappointed to discover that the article on Swainson in the historians’ bible, the
Dictionary of Scientific Biography
(called the
DSB
by all pros), follows the old tradition, criticized earlier in this essay, of dismissing superseded systems as pathetically foolish in the light of modern knowledge:
His indefatigable pursuit of natural history and conscientious labor on its behalf deserve to be remembered as a set-off against the injury he unwittingly caused by his adherence to the absurd quinary system…. This extraordinary theory was pertinaciously held by Swainson throughout his zoological career and it certainly impaired much of his work.
Oken and Swainson were severely and legitimately criticized in their own terms. (I have tried to raise some of these arguments by exposing the fanciful criteria used to establish circles of five and to draw analogies between them.) But they were not fools or madmen, and their systems were not absurd. Oken and Swainson ranked highly among the best natural historians of Europe, and their numerical systems of taxonomy were popular and serious contenders among contemporary schemes for ordering nature.
Rigid numerical systems only become absurd in the later light of evolution, for their respectability hinges upon
theories
favored for the causes of nature’s order. If God placed species on earth (as Swainson believed), then he might have acted with a numerical precision displaying the rigor and harmony of his thoughts. If simple laws, rather than accidents of history, establish the sequence of organisms (as Oken held), then numerical order might arise among animals just as the periodic table regulates chemical elements. Numerology in taxonomy may be dismissed as absurd mysticism today, but in Oken and Swainson’s time, this approach embodied a reasonable result of defensible theories about the causes of nature’s order. Swainson put it right on the line when he inferred from quinary order both God’s existence and his special concern for us:
When we discover evident indications of a definite plan, upon which all these modifications have been regulated by a few simple and universal laws, our wonder is as much excited at the inconceivable wisdom and goodness of the SUPREME by whom these myriads of beings have been created and are now preserved, as at the mental blindness and perverted understanding of those philosophers, falsely so called, who would persuade us, that even Man, the last and best of created things, is too insignificant for the special care of Omnipotence.
Darwin destroyed the rule of five forever because he removed its rationale by reconstructing nature. His agent of destruction was not evolution itself. I can imagine evolutionary theories (indeed some have been proposed) so committed to foreordination by simple laws or directing intelligences that numerical order might still emerge from rigidly predictable process. Darwin’s exterminating angel was, simply, history. Evolution does not unroll according to simple laws specifying necessary results. It follows the vagaries of history. Its pathways are twisted and churned by changing environments, from minor shifts in temperature and precipitation to the rise of mountain chains, the growth of glaciers, the drift of continents, and even (probably) the impact of comets or asteroids. Evolution cannot achieve engineering perfection because it must work with inherited parts available from previous histories in different contexts: the panda’s “thumb” is a clumsy, detached wrist bone, pressed into service because the true first digit became committed to other functions during ancestral life as a conventional carnivore; we suffer the pain of aching backs and the annoyances of hernias because large four-footed creatures of our lineage were not really made to walk on their toes—four legs good, two legs not so good.
How could animals evolve along the tortuous pathways of history and arrange themselves neatly into circles of five? Numerical precision cannot regulate taxonomy because life unfolds in time. Evolution records a complex, irrevocable history; its pathways were not preordained by simple rules or commanding intelligences.
But life regulated by history still has order—firm, ineluctable, definite, testable pattern. Its order is the topology of its proper metaphor—the tree of life. Its order is genealogy, connection by branching and descent. Swainson
described
the biological world correctly before he went too far:
Had the order of nature been so irregular that we had found she created some birds with four feet, others with two, and some with none; or that, like the fabulous griffin, there were creatures half quadruped, half bird; or, if insects had been found with the feet of quadrupeds, and the toes of birds; in short, had such compounds in the animal world existed, the foundations of natural history, as a science, could never have been laid.
Darwin then found the
reason
for order and changed our world forever:
Something more is included in our classification than mere resemblance. I believe that something more is…propinquity of descent,—the only known cause of the similarity of organic beings.
I WISH TO PROPOSE
a new kind of explanation for the oldest chestnut of the hot stove league—the most widely discussed trend in the history of baseball statistics: the extinction of the .400 hitter. Baseball aficionados wallow in statistics, a sensible obsession that outsiders grasp with difficulty and ridicule often. The reasons are not hard to fathom. In baseball, each essential action is a contest between two individuals—batter and pitcher, or batter and fielder—thus creating an arena of truly individual achievement within a team sport.
The abstraction of personal achievement in other team sports makes comparatively little sense. Goals scored in basketball or yards gained in football depend on the indissoluble intricacy of team play; a home run is you against him. Moreover, baseball has been played under a set of rules and conditions sufficiently constant during our century to make comparisons meaningful, yet sufficiently different in detail to provide endless grist for debate (the “dead ball” of 1900–1920 versus the “lively ball” of later years, the introduction of night games and relief pitchers, the invention of the slider, the changing and irregular sizes of ball parks, nature’s own versus Astroturf).
No subject has inspired more argument than the decline and disappearance of the .400 hitter—or, more generally, the drop in league-leading batting averages during our century. Since we wallow in nostalgia and have a lugubrious tendency to compare the present unfavorably with a past “golden era,” this trend acquires all the more fascination because it carries moral implications linked metaphorically with junk foods, nuclear bombs, and eroding environments as signs of the current decline and impending fall of Western civilization.
Between 1901 and 1930, league-leading averages of .400 or better were common enough (nine out of thirty years) and achieved by several players (Lajoie, Cobb, Jackson, Sisler, Heilmann, Hornsby, and Terry), and averages over .380 scarcely merited extended commentary. Yet the bounty dried up abruptly thereafter. In 1930 Bill Terry hit .401 to become the last .400 hitter in the National League; and Ted Williams’s .406 in 1941 marked the last pinnacle for the American League. Since Williams, the greatest hitter I ever saw, attained this goal in the year I was born (and I am, alas, no spring chicken), only three men have hit higher than .380 in a single season: Williams again in 1957 (.388, at age thirty-nine, with my vote for the greatest batting accomplishment of our era), Rod Carew (.388 in 1977), and George Brett (.390 in 1980). Where have all the hitters gone?
League averages for our century
American League | National League | |
1901–1910 | .251 | .253 |
1911–1920 | .259 | .257 |
1921–1930 | .286 | .288 |
1931–1940 | .279 | .272 |
1941–1950 | .260 | .260 |
1951–1960 | .257 | .260 |
1961–1970 | .245 | .253 |
1971–1980 | .258 | .256 |
Two rather different kinds of explanation have been traditionally offered. The first, naïve and moral, simply acknowledges with a sigh that there were giants on the earth in those days. Something in us needs to castigate the present in the light of an unrealistically rosy past. In researching the history of misconduct, for example, I discovered that every generation (at least since the mid-nineteenth century) has imagined itself engulfed in a crime wave. Each age has also witnessed a shocking decline in sportsmanship. Similarly, senior citizens of the hot stove league, and younger fans as well (for nostalgia may have its greatest emotional impact on those too young to know a past reality directly), tend to argue that the .400 hitters of old simply cared more and tried harder. Well, Ty Cobb may have been a paragon of intensity and a bastard to boot, and Pete Rose may be a gentleman by comparison, but today’s play is anything but lackadaisical. Say what you will; monetary rewards in the millions do inspire single-minded effort.
The second kind of explanation views people as much of a muchness over time and attributes the downward trend in league-leading batting to changes in the game and its styles of play. Most often cited are improvements in pitching and fielding, and more grueling schedules that shave off the edge of excellence. J.L. Reichler, for example, one of baseball’s premier record keepers, argues (see bibliography):
The odds are heavily against another .400 hitter because of the tremendous improvement in relief pitching and fielding. Today’s players face the additional handicaps of a longer schedule, which wears down even the strongest players, and more night games, in which the ball is harder to see.
I do not dispute Reichler’s factors, but I believe that he offers an incomplete explanation, expressed from an inadequate perspective.
Another proposal in this second category invokes the numerology of baseball. Every statistics maven knows that, following the introduction of the lively ball in the early 1920s (and Babe Ruth’s mayhem upon it), batting averages soared in general and remained high for twenty years. As the accompanying chart shows, league averages for all players rose into the .280s in both leagues during the 1920s and remained in the .270s during the 1930s, but never topped .260 in any other decade of our century. Naturally, if league averages rose so substantially, we should not be surprised that the best hitters also improved their scores. The great age of .400 hitting in the National League did occur during the 1920s (another major episode of high averages occurred in the pre-modern era, during the 1890s, when the decadal average rose to .280—it had been .259 for the 1870s and .254 for the 1880s).
But this simple factor cannot explain the extinction of .400 hitting either. No one hit .400 in either league during 1931–1940, even though league averages stood twenty points above their values for the first two decades of our century, when fancy hitting remained in vogue. A comparison of these first two decades with recent times underscores both the problem and the failure of resolutions usually proposed—for high hitting in general (and .400 hitting in particular) flourished from 1900 to 1920, but league averages back then did not differ from those for recent decades, while high hitting has gone the way of bird’s teeth.
Consider, for example, the American League during 1911–1920 (league average of .259) and 1951–1960 (league average of .257). Between 1911 and 1920, averages above .400 were recorded during three years, and the leading average dipped below .380 only twice (Cobb’s .368 and .369 in 1914 and 1915). This pattern of high averages was not just Ty Cobb’s personal show. In 1912 Cobb hit .410, while the ill-fated Shoeless Joe Jackson reached .395, Tris Speaker .383, thirty-seven-year-old Nap Lajoie .368, and Eddie Collins .348. By comparison, during 1951–1960, only three leading averages exceeded Eddie Collins’s fifth-place .348 (Mantle’s .353 in 1956, Kuenn’s .353 in 1959, and Williams’s .388, already discussed, in 1957). The 1950s, by the way, was not a decade of slouches, what with the likes of Mantle, Williams, Minoso, and Kaline. Thus, a general decline in league-leading averages throughout the century cannot be explained by an inflation of general averages during two middle decades. We are left with a puzzle. As with most persistent puzzles, we probably need new
kind
of explanation, not merely a recycling and refinement of old arguments.
I am a paleontologist by trade. We students of life’s history spend most of our time worrying about long-term trends. Has life become more complex through time? Do more species of animals live now than 200 million years ago? Several years ago, it occurred to me that we suffer from a subtle but powerful bias in our approach to explaining trends. Extremes fascinate us (the biggest, the smallest, the oldest), and we tend to concentrate on them alone, divorced from the systems that include them as unusual values. In explaining extremes, we abstract them from larger systems and assume that their trends arise for self-generated reasons: if the biggest become bigger through time, some powerful advantage must accompany increasing size.
But if we consider extremes as the limiting values of larger systems, a very different kind of explanation often applies. If the
amount of variation
within a system changes (for whatever reason), then extreme values may increase (if total variation grows) or decrease (if total variation declines) without any special reason rooted in the intrinsic character or meaning of the extreme values themselves. In other words,
trends in extremes
may result from systematic changes in
amounts of variation
. Reasons for changes in variation are often rather different from proposed (and often spurious) reasons for changes in extremes considered as independent from their systems.
Let me illustrate this unfamiliar concept with two examples from my own profession—one for increasing, the other for decreasing extreme values. First, an example of increasing extreme values properly interpreted as an expansion of variation: The largest mammalian brain sizes have increased steadily through time (the brainiest have gotten brainier). Many people infer from this fact that inexorable trends to increasing brain size affect most or all mammalian lineages. Not so. Within many groups of mammals, the most common brain size has not changed at all since the group became established. Variation among species has, however, increased—that is, the range of brain sizes has grown as species become more numerous and more diverse in their adaptations. If we focus only on extreme values, we see a general increase through time and assume some intrinsic and ineluctable value in growing braininess. If we consider variation, we see only an expansion in range through time (leading, of course, to larger extreme values), and we offer a different explanation based on the reasons for increased diversity.
Second, an example of decreasing extremes properly interpreted as declining variation: A characteristic pattern in the history of most marine invertebrates has been called “early experimentation and later standardization.” When a new body plan first arises, evolution seems to explore all manner of twists, turns, and variations. A few work well, but most don’t (see essay 16). Eventually, only a few survive. Echinoderms now come in five basic varieties (two kinds of starfish, sea urchins, sea cucumbers, and crinoids—an unfamiliar group, loosely resembling many-armed starfish on a stalk). But when echinoderms first evolved, they burst forth in an astonishing array of more than twenty basic groups, including some coiled like a spiral and others so bilaterally symmetrical that a few paleontologists have interpreted them as the ancestors of fish. Likewise, mollusks now exist as snails, clams, cephalopods (octopuses and their kin), and two or three other rare and unfamiliar groups. But they sported ten to fifteen other fundamental variations early in their history. This trend towards shaving and elimination of extremes is surely the more common in nature. When systems first arise, they probe all the limits of possibility. Many variations don’t work; the best solutions emerge, and variation diminishes. As systems regularize, their variation decreases.
From this perspective, it occurred to me that we might be looking at the problem of .400 hitting the wrong way round. League-leading averages are extreme values within systems of variation. Perhaps their decrease through time simply records the standardization that affects so many systems as they stabilize—including life itself as stated above and developed in essay 16. When baseball was young, styles of play had not become sufficiently regular to foil the antics of the very best. Wee Willie Keeler could “hit ’em where they ain’t” (and compile an average of .432 in 1897) because fielders didn’t yet know where they should be. Slowly, players moved toward optimal methods of positioning, fielding, pitching, and batting—and variation inevitably declined. The best now met an opposition too finely honed to its own perfection to permit the extremes of achievement that characterized a more casual age. We cannot explain the decrease of high averages merely by arguing that managers invented relief pitching, while pitchers invented the slider—conventional explanations based on trends affecting high hitting considered as an independent phenomenon. Rather, the entire game sharpened its standards and narrowed its ranges of tolerance.
Thus I present my hypothesis: The disappearance of the .400 hitter (and the general decline of league-leading averages through time) is largely the result of a more general phenomenon—a decrease in the variation of batting averages as the game standardized its methods of play—and not an intrinsically driven trend warranting a special explanation in itself.
To test such a hypothesis, we need to examine changes through time in the difference between league-leading batting averages and the general average for all batters. This difference must decrease if I am right. But since my hypothesis involves an entire system of variation, then, somewhat paradoxically, we must also examine differences between
lowest
batting averages and the general average. Variation must decrease at both ends—that is, within the entire system. Both highest and lowest batting averages must converge toward the general league average.
I therefore reached for my trusty
Baseball Encyclopedia
, that
vade mecum
for all serious fans (though, at more than 2,000 pages, you can scarcely tote it with you). The encyclopedia reports league averages for each year and lists the five highest averages for players with enough official times at bat. Since high extremes fascinate us while low values are merely embarrassing, no listing of the lowest averages appears, and you have to make your way laboriously through the entire roster of players. For lowest averages, I found (for each league in each year) the five bottom scores for players with at least 300 at bats. Then, for each year, I compared the league average with the average of the five highest and five lowest scores for regular players. Finally, I averaged these yearly values decade by decade.
