Statistics Essentials For Dummies (35 page)

3. Calculate the standard error:
.
4. Divide your result from Step 2 by your result from Step 3.
To interpret the test statistic, look up your test statistic on the standard normal distribution (see Table A-1 in the appendix) and calculate the
p
-value. For example, suppose Cavifree toothpaste claims that four out of five dentists recommend Cavifree toothpaste to their patients. In this case, the population is all dentists, and
p
is the proportion of all dentists who recommended Cavifree to their patients. The claim is that
p
is equal to "four out of five," which means that
p
o
is 4/5 = 0.80. You suspect that the proportion is actually less than 0.80. Your hypotheses are H
o
:
p
= 0.80 versus H
a
:
p
< 0.80. Suppose that 150 out of 200 dental patients sampled received a recommendation for Cavifree.
To find the test statistic, observe that the sample proportion
is 150/200 = 0.75. Since
p
o
= 0.80,take 0.75 - 0.80 = -0.05 as your numerator. Next, the standard error is the square root of [(0.80 ∗ [1 - 0.80])/200] = the square root of (0.16/200) = the square root of 0.0008 = 0.028.The test statistic is -0.05 divided by 0.028, which is -0.05/0.028 = -1.79. This means that your sample results are 1.79 standard errors below the claimed value for the population.
How often would you expect to get results like this if H
o
were true? The percentage chance of being at or beyond (in this case to the left of ) -1.79, is 3.67% . (Look up -1.79 in Table A-1 in the appendix and use the corresponding percentile, because H
a
is a less-than hypothesis. Now divide by 100 to get your
p
-value, which is 0.0367 . Because the
p
-value is less than 0.05, you have enough evidence to reject H
o
. According to your sample, the claim of four out of five (80% of) dentists recommending Cavifree toothpaste is not true; the actual percentage of recommendations is less than that.
Comparing Two Population Means
This test is used when the variable is numerical (for example, income, cholesterol level, or miles per gallon) and two populations or groups are being compared (for example, cars versus SUVs). Two separate random samples need to be selected, one from each population, in order to collect the data needed for this test. The null hypothesis is that the two population means are the same; in other words, that their difference is equal to 0. The notation for the null hypothesis is H
o
:
μ
x
-
μ
y
= 0, where
μ
x
is the mean of the first population, and
μ
y
is the mean of the second population.
The test statistic comparing two means is:
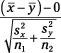
To calculate it, do the following:
1. Calculate the sample means (
and
) and sample standard deviations (
s
x
and
s
y
) for each sample separately. Let
n
1
and
n
2
represent the two sample sizes (they need not be equal).
See Chapter 1 for these calculations.
2. Find the difference between the two sample means,
-
.
3.
Calculate the standard error,.
4. Divide your result from Step 2 by your result from Step 3.
To interpret the test statistic, look up your test statistic on the t-distribution with n1 + n2 -2 degrees of freedom (see Table A-2 in the appendix) and calculate the
p
-value. For example, suppose you want to compare the absorbency of two brands of paper towels (call the brands Stats-absorbent and Sponge-o-matic). You can make this comparison by looking at the average number of ounces each brand can absorb before being saturated. H
o
says the difference between the average absorbencies is 0 (non-existent), and H
a
says the difference is not 0. In other words, H
o
:
μ
x
-
μ
y
= 0 versus H
o
:
μ
x
-
μ
y
≠
0. Here, you have no indication of which paper towel may be more absorbent, so the not-equal-to alternative is the one to use.
