In Pursuit of the Unknown (31 page)

Any pattern in space and time can be thought of as a superposition of sinusoidal patterns with different frequencies.

The component frequencies can be used to analyse the patterns, create them to order, extract important features, and remove random noise.

Fourier's technique is very widely used, for example in image processing and quantum mechanics. It is used to find the structure of large biological molecules like DNA, to compress image data in digital photography, to clean up old or damaged audio recordings, and to analyse earthquakes. Modern variants are used to store fingerprint data efficiently and to improve medical scanners.

N
ewton's
Principia
opened the door to the mathematical study of nature, but his fellow countrymen were too obsessed with the priority dispute over calculus to find out what lay beyond. While England's finest were seething over what they perceived to be disgraceful allegations about the country's greatest living mathematician – much of it probably his own fault for listening to well-intentioned but foolish friends – their continental colleagues were extending Newton's ideas about laws of nature to most of the physical sciences. The wave equation was quickly followed by remarkably similar equations for gravitation, electrostatics, elasticity, and heat flow. Many bore the names of their inventors: Laplace's equation, Poisson's equation. The equation for heat does not; it bears the unimaginative and not entirely accurate name ‘heat equation'. It was introduced by Joseph Fourier, and his ideas led to the creation of a new area of mathematics whose ramifications were to spread far beyond its original source. Those ideas could have been triggered by the wave equation, where similar methods were floating around in the collective mathematical consciousness, but history plumped for heat.

The new method had a promising beginning: in 1807 Fourier submitted an article on heat flow to the French Academy of Sciences, based on a new partial differential equation. Although that prestigious body declined to publish the work, it encouraged Fourier to develop his ideas further and try again. At that time the Academy offered an annual prize for research on whatever topic they felt was sufficiently interesting, and they made heat the topic of the 1812 prize. Fourier duly submitted his revised and extended article, and won. His heat equation looks like this:

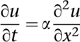
Here
u
(
x
,
t
) is the temperature of a metal rod at position
x
and time
t
, considering the rod to be infinitely thin, and α is a constant, the thermal
diffusivity. So it really ought to be called the temperature equation. He also developed a higher-dimensional version,

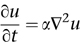
valid on any specified region of the plane or space.

The heat equation bears an uncanny resemblance to the wave equation, with one crucial difference. The wave equation uses the second time derivative
∂
²
u/∂t
²
but in the heat equation this is replaced by the first derivative
∂u/∂t
. This change may seem small, but its physical meaning is huge. Heat does not persist indefinitely, in the way that a vibrating violin string continues to vibrate forever (according to the wave equation, which assumes no friction or other damping). Instead, heat dissipates, dies away, as time passes, unless there is some heat source that can top it up. So a typical problem might be: heat one end of a rod to keep its temperature steady, cool the other end to do the same, and find out how the temperature varies along the rod when it settles to a steady state. The answer is that it falls off exponentially. Another typical problem is to specify the initial temperature profile along the rod, and then ask how it changes as time passes. Perhaps the left half starts at a high temperature and the right half at a cooler one; the equation then tells us how the heat from the hot part diffuses into the cooler part.

The most intriguing aspect of Fourier's prizewinning memoir was not the equation, but how he solved it. When the initial profile is a trigonometric function, such as sin
x
, it is easy (to those with experience in such matters) to solve the equation, and the answer is
e
^−αt
sin
x
. This resembles the fundamental mode of the wave equation, but there the formula was sin
ct
sin
x
. The eternal oscillation of a violin string, corresponding to the sin
ct
factor, has been replaced by an exponential, and the minus sign in the exponent
−αt
tells us that the entire temperature profile dies away at the same rate, all along the rod. (The physical difference here is that waves conserve energy, but heat flow does not.) Similarly, for a profile sin 5
x
, say, the solution is e
^{−25αt}
sin 5
x
, which also dies out, but at a much faster rate. The 25 is 5
²
, and this is an example of a general pattern, applicable to initial profiles of the form sin
nx
or cos
nx
.
¹
To solve the heat equation, just multiply by
e
^{−n
2
αt}
.

Now the story follows the same general outline as the wave equation.
The heat equation is linear, so we can superpose solutions. If the initial profile is

u(x
, 0) = sin
x
+ sin 5
x

then the solution is

u
(
x
,
t
) = e
^-αt
sin
x
+ e
^-25αt
sin 5
x

and each mode dies way at a different rate. But initial profiles like this are a bit artificial. To solve the problem I mentioned earlier, we want an initial profile where
u(x
, 0) = 1 for half the rod but –1 for the other half. This profile is discontinuous, a square wave in engineering terminology. But sine and cosine curves are continuous. So no superposition of sine and cosine curves can represent a square wave.

No finite superposition, certainly. But, again, what if we allowed
infinitely many
terms? Then we can try to express the initial profile as an infinite series, of the form

u(x
, 0) =
a
₀
+ a
₁
cos
x
+
a
₂
cos 2
x
+ a
₃
cos 3
x
+ . . .

+
b
₁
sin
x
+
b
₂
sin 2
x
+
b
₃
sin 3
x
+ . . .

for suitable constants
a
₀
,
a
₁
,
a
₂
,
a
₃
, …,
b
1,
b
2,
b
3, … . (There is no
b
₀
because sin 0
x
= 0.) NOW it does seem possible to get a square wave (see
Figure 40
). In fact, most coefficients can be set to zero. Only the
b
_n
for
n
odd are needed, and then
b
_n
= 8/
n
π.

Fig 40
How to get a square wave from sines and cosines.
Left
: The component sinusoidal waves.
right
: Their sum and a square wave. Here we show the first few terms of the Fourier series. Additional terms make the approximation to a square wave ever better.

Fourier even had general formulas for the coefficients
a
_n
and
b
_n
for a general profile
f
(
x
), in terms of integrals:

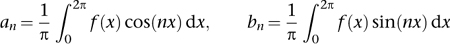
After a lengthy trek through power series expansions of trigonometric functions, he realised that there was a much simpler way to derive these formulas. If you take two different trigonometric functions, say cos
2x
and sin 5
x
, multiply them together, and integrate from 0 to 2π, you get zero. This is even the case when they look like cos 5
x
and sin 5
x
. But if they are the same – say both equal to sin 5
x
– the integral of their product is not zero. In fact, it is
π
. If you start by assuming that
f
(
x
) is the sum of a trigonometric series, multiply everything by sin 5
x
, and integrate, all of the terms disappear except for the one corresponding to sin 5
x
, namely b
₅
sin 5
x
. Here the integral is
π
. Divide by that, and you have Fourier's formula for
b
₅
. The same goes for all the other coefficients.

Although it won the academy's prize, Fourier's memoir was roundly criticised for being insufficiently rigorous, and the academy declined to publish it. This was highly unusual and it greatly irritated Fourier, but the academy held its ground. Fourier was incensed. Physical intuition told him he was right, and if you plugged his series into this equation it was clearly a solution. It
worked
. The real problem was that unwittingly he had reopened an old wound. As we saw in
Chapter 8
, Euler and Bernoulli had been arguing for ages about a similar issue for the wave equation, where Fourier's exponential dissipation over time was replaced by an unending sinusoidal oscillation in the wave amplitude. The underlying mathematical issues were identical. In fact, Euler had already published the integral formulas for the coefficients in the context of the wave equation.