In Pursuit of the Unknown (35 page)

In the earliest days of aircraft design, pioneers put their aeroplanes together using back-of-the-envelope calculations, physical intuition, and trial and error. When your aim was to fly more than a hundred metres no more than three metres off the ground, that was good enough. The first time that
Wright Flyer I
got properly off the ground, instead of stalling and crashing after three seconds in the air, it travelled 120 feet at a speed just below 7 mph. Orville, the pilot on that occasion, managed to keep it aloft for a staggering 12 seconds. But the size of passenger aircraft quickly grew, for economic reasons: the more people you can carry in one flight, the more profitable it will be. Soon aircraft design had to be based on a more rational and reliable method. The science of aerodynamics was born, and its basic mathematical tools were equations for fluid flow. Since air is both viscous and compressible, the Navier–Stokes equation, or some simplification that makes sense for a given problem, took centre stage as far as theory went.

However, solving those equations, in the absence of modern computers, was virtually impossible. So the engineers resorted to an analogue computer: placing models of the aircraft in a wind tunnel. Using a few general properties of the equations to work out how variables change as the scale of the model changes, this method provided basic information
quickly and reliably. Most Formula 1 teams today use wind tunnels to test their designs and evaluate potential improvements, but computer power is now so great that most also use CFD. For example,
Figure 43
shows a CFD calculation of air flow past a BMW Sauber car. As I write, one team, Virgin Racing, uses only CFD, but they will be using a wind tunnel as well next year.

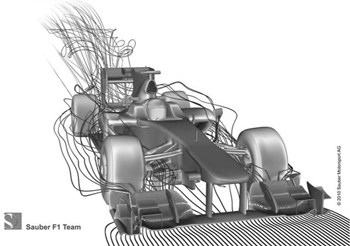
Fig 43
Computed air flow past a Formula 1 car.

Wind tunnels are not terribly convenient; they are expensive to build and run, and they need lots of scale models. Perhaps the biggest difficulty is to make accurate measurements of the flow of air without affecting it. If you put an instrument in the wind tunnel to measure, say, air pressure, then the instrument itself disturbs the flow. Perhaps the biggest practical advantage of CFD is that you can calculate the flow without affecting it. Anything you might wish to measure is easily available. Moreover, you can modify the design of the car, or a component, in software, which is a lot quicker and cheaper than making lots of different models. Modern manufacturing processes often involve computer models at the design stage anyway.

Supersonic flight, where the aircraft goes faster than sound, is especially tricky to study using models in a wind tunnel, because the wind speeds are so great. At such speeds, the air cannot move away from the aircraft as quickly as the aircraft pushes itself through the air, and this
causes shockwaves – sudden discontinuities in air pressure, heard on the ground as a sonic boom. This environmental problem was one reason why the joint Anglo-French airliner Concorde, the only supersonic commercial aircraft ever to go into service, had limited success: it was not allowed to fly at supersonic speeds except over oceans. CFD is widely used to predict the flow of air past a supersonic aircraft.

There are about 600 million cars on the planet and tens of thousands of civil aircraft, so even though these applications of CFD may seem high-tech, they are significant in everyday life. Other ways to use CFD have a more human dimension. It is widely used by medical researchers to understand blood flow in the human body, for example. Heart malfunction is one of the leading causes of death in the developed world, and it can be triggered either by problems with the heart itself or by clogged arteries, which disrupt the blood flow and can cause clots. The mathematics of blood flow in the human body is especially intractable analytically because the walls of the arteries are elastic. It's difficult enough to calculate the movement of fluid through a rigid tube; it's much harder if the tube can change its shape depending on the pressure that the fluid exerts, because now the domain for the calculation doesn't stay the same as time passes. The shape of the domain affects the flow pattern of the fluid, and simultaneously the flow pattern of the fluid affects the shape of the domain. Pen-and-paper mathematics can't handle that sort of feedback loop.

CFD is ideal for this kind of problem because computers can perform billions of calculations every second. The equation has to be modified to include the effects of elastic walls, but that's mostly a matter of extracting the necessary principles from elasticity theory, another well-developed part of classical continuum mechanics. For example, a CFD calculation of how blood flows through the aorta, the main artery entering the heart, has been carried out at the École Polytechnique Féderale de Lausanne in Switzerland. The results provide information that can help doctors get a better understanding of cardiovascular problems.

They also help engineers to develop improved medical devices such as stents – small metal-mesh tubes that keep the artery open. Suncica Canic has used CFD and models of elastic properties to design better stents, deriving a mathematical theorem that caused one design to be abandoned and suggested better designs. Models of this type have become so accurate that the US Food and Drugs Administration is considering requiring any
group designing stents to carry out mathematical modelling before performing clinical trials. Mathematicians and doctors are joining forces to use the Navier–Stokes equation to obtain better predictions of, and better treatments for, the main causes of heart attacks.

Another, related, application is to heart bypass operations, in which a vein is removed from elsewhere in the body and grafted into the coronary artery. The geometry of the graft has a strong effect on the blood flow. This in turn affects clotting, which is more likely if the flow has vortices because blood can become trapped in a vortex and fail to circulate properly. So here we see a direct link between the geometry of the flow and potential medical problems.

The Navier–Stokes equation has another application: climate change, otherwise known as global warming. Climate and weather are related, but different. Weather is what happens at a given place, at a given time. It may be raining in London, snowing in New York, or baking in the Sahara. Weather is notoriously unpredictable, and there are good mathematical reasons for this: see
Chapter 16
on chaos. However, much of the unpredictability concerns small-scale changes, both in space and time: the fine details. If the TV weatherman predicts showers in your town tomorrow afternoon and they happen six hours later and 20 kilometres away, he thinks he did a good job and you are wildly unimpressed. Climate is the long-term ‘texture' of weather – how rainfall and temperature behave when averaged over long periods, perhaps decades. Because climate averages out these discrepancies, it is paradoxically easier to predict. The difficulties are still considerable, and much of the scientific literature investigates possible sources of error, trying to improve the models.

Climate change is a politically contentious issue, despite a very strong scientific consensus that human activity over the past century or so has caused the average temperature of the Earth to rise. The increase to date sounds small, about 0.75 degrees Celsius during the twentieth century, but the climate is very sensitive to temperature changes on a global scale. They tend to make the weather more extreme, with droughts and floods becoming more common.

‘Global warming' does not imply that the temperature everywhere is changing by the same tiny amount. On the contrary, there are large fluctuations from place to place and from time to time. In 2010 Britain experienced its coldest winter for 31 years, prompting the
Daily Express
to print the headline ‘and
still
they claim it's global warming'. As it happens,
2010 tied with 2005 as the hottest year on record, across the globe.
¹
So ‘they' were right. In fact, the cold snap was caused by the jet stream changing position, pushing cold air south from the Arctic, and this happened because the Arctic was unusually
warm
. Two weeks of frost in central London does not disprove global warming. Oddly, the same newspaper reported that Easter Sunday 2011 was the hottest on record, but made no connection to global warming. On that occasion they correctly distinguished weather from climate. I'm fascinated by the selective approach.

Similarly, ‘climate change' does not simply mean that the climate is changing. It has done that without human assistance repeatedly, mainly on long timescales, thanks to volcanic ash and gases, long-term variations in the Earth's orbit around the Sun, even India colliding with Asia to create the Himalayas. In the context currently under debate, ‘climate change' is short for ‘anthropogenic climate change' – changes in global climate caused by human activity. The main causes are the production of two gases: carbon dioxide and methane. There are greenhouse gases: they trap incoming radiation (heat) from the Sun. Basic physics implies that the more of these gases the atmosphere contains, the more heat it traps; although the planet does radiate some heat away, on balance it will get warmer. Global warming was predicted, on this basis, in the 1950s, and the predicted temperature increase is in line with what has been observed.

The evidence that carbon dioxide levels have increased dramatically comes from many sources. The most direct is ice cores. When snow falls in the polar regions, it packs together to form ice, with the most recent snow at the top and the oldest at the bottom. Air is trapped in the ice, and the conditions that prevail there leave it virtually unchanged for very long periods of time, keeping the original air in and more recent air out. With care, it is possible to measure the composition of the trapped air and to determine the date when it was trapped, very accurately. Measurements made in the Antarctic show that the concentration of carbon dioxide in the atmosphere was pretty much constant over the past 100,000 years – except for the last 200, when it shot up by 30%. The source of the excess carbon dioxide can be inferred from the proportions of carbon-13, one of the isotopes (different atomic forms) of carbon. Human activity is by far the most likely explanation.

The main reason why the skeptics have even faint glimmerings of a case is the complexity of climate forecasting. This has to be done using mathematical models, because it's about the future. No model can include every single feature of the real world, and, if it did, you could never work
out what it predicted, because no computer could ever simulate it. Every discrepancy between model and reality, however insignificant, is music to the skeptics' ears. There is certainly room for differences of opinion about the likely effects of climate change, or what we should do to mitigate it. But burying our heads in the sand isn't a sensible option.

Two vital aspects of climate are the atmosphere and the oceans. Both are fluids, and both can be studied using the Navier–Stokes equation. In 2010 the UK's main science funding body, the Engineering and Physical Sciences Research Council, published a document on climate change, singling out mathematics as a unifying force: ‘Researchers in meteorology, physics, geography and a host of other fields all contribute their expertise, but mathematics is the unifying language that enables this diverse group of people to implement their ideas in climate models.' The document also explained that ‘The secrets of the climate system are locked away in the Navier–Stokes equation, but it is too complex to be solved directly.' Instead, climate modellers use numerical methods to calculate the fluid flow at the points of a three-dimensional grid, covering the globe from the ocean depths to the upper reaches of the atmosphere. The horizontal spacing of the grid is 100 kilometres – anything smaller would make the computations impractical. Faster computers won't help much, so the best way forward is to think harder. Mathematicians are working on more efficient ways to solve the Navier–Stokes equation numerically.

The Navier–Stokes equation is only part of the climate puzzle. Other factors include heat flow within and between the oceans and the atmosphere, the effect of clouds, non-human contributions such as volcanoes, even aircraft emissions in the stratosphere. Skeptics like to emphasise such factors to suggest the models are wrong, but most of them are known to be irrelevant. For example, every year volcanoes contribute a mere 0.6% of the carbon dioxide produced by human activity. All of the main models suggest that there is a serious problem, and humans have caused it. The main question is just how much the planet will warm up, and what level of disaster will result. Since perfect forecasting is impossible, it is in everybody's interests to make sure that our climate models are the best we can devise, so that we can take appropriate action. As the glaciers melt, the Northwest Passage opens up as Arctic ice shrinks, and Antarctic ice shelves are breaking off and sliding into the ocean, we can no longer take the risk of believing that we don't need to do anything and it will all sort itself out.