In Pursuit of the Unknown (14 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

It was often possible to calculate good
approximations
to the motion (which often solved the problem for practical purposes), but there no longer seemed to be an exact formula. This problem bedevilled even simplified versions, such as the restricted three-body problem. Suppose that a planet orbits a star in a perfect circle: how will a speck of dust, of negligible mass, move?
Calculating approximate orbits for three or more bodies, by hand, using pencil and paper, was just about feasible, but very laborious. Mathematicians devised innumerable tricks and short cuts, leading to a reasonable understanding of several astronomical phenomena. Only in the late nineteenth century did the true complexity of the three-body problem become apparent, when Henri Poincaré realised that the geometry involved was necessarily extraordinarily intricate. And only in the late twentieth century did the advent of powerful computers reduce the labour of hand calculations, permitting accurate long-term predictions of the motion of the Solar System.
Â
Poincaré's breakthrough â if it can be called that, since at the time it seemed to be telling everyone that the problem was hopeless and it was pointless to seek a solution â came about because he competed for a mathematical prize. Oscar II, king of Sweden and Norway, announced a
competition to celebrate his 60th birthday in 1889. Taking advice from the mathematician Gösta Mittag-Leffler, the king chose the general problem of arbitrarily many bodies moving under Newtonian gravitation. Since it was well understood that an explicit formula akin to the two-body ellipse was an unrealistic aim, the requirement was relaxed: the prize would be awarded for an approximation method of a very specific kind. Namely, the motion must be determined as an infinite series, giving results as accurate as we please if enough terms are included.
Poincaré did not answer this question. Instead, his memoir on the topic, published in 1890, provided evidence that it might not possess that kind of answer, even for just three bodies â star, planet, and dust particle. By thinking about the geometry of hypothetical solutions, Poincaré discovered that in some cases the orbit of the dust particle must be exceedingly complex and tangled. He then, in effect, threw up his hands in horror and made the pessimistic statement that âWhen one tries to depict the figure formed by these two curves and their infinity of intersections, each of which corresponds to a doubly asymptotic solution, these intersections form a kind of net, web or infinitely tight mesh. . . One is struck by the complexity of this figure that I am not even attempting to draw.'
We now see Poincaré's work as a breakthrough, and discount his pessimism, because the complicated geometry that led him to despair of ever solving the problem actually provides powerful insights if it is properly developed and understood. The complex geometry of the associated dynamics turned out to be one of the earliest examples of
chaos:
the occurrence, in non-random equations, of solutions so complicated that in some respects they appear to be random, see
Chapter 16
.
There are several ironies in the story. Mathematical historian June Barrow-Green discovered that the published version of Poincaré's prizewinning memoir was not the one that won the prize.
4
This earlier version contained a major error, overlooking the chaotic solutions. The work was at proof stage when an embarrassed Poincaré realised his blunder, and he paid for a new printing of a corrected version. Almost all copies of the original were destroyed, but one remained tucked away in the archives of the Mittag-Leffler Institute in Sweden, where Barrow-Green found it.
It also turned out that the presence of chaos does not, in fact, rule out series solutions, but these are valid almost always rather than always. Karl Frithiof Sundman, a Finnish mathematician, discovered this in 1912 for the three-body problem, using series formed from powers of the cube root
of time. (Powers of time won't hack it.) The series converge â have a sensible sum â unless the initial state has zero angular momentum, but such states are infinitely rare, in the sense that a random choice of angular momentum is almost always nonzero. In 1991 the Chinese mathematician Qiudong Wang extended these results to any number of bodies, but did not classify the rare exceptions when the series fail to converge. Such a classification is likely to be very complicated: it must include solutions where bodies escape to infinity in finite time, or oscillate ever faster, both of which can happen for five or more bodies.
Â
Newton's law of gravity is routinely applied to design orbits for space missions. Here even two-body dynamics is useful in its own right. In its early days, the exploration of the Solar System mainly used two-body orbits, segments of ellipses. By burning its rockets the spacecraft could be switched from one ellipse to a different one. But as the aims of space programmes got more ambitious, more efficient methods were needed. They came from many-body dynamics, usually three bodies but occasionally as great as five. The new methods of chaos and topological dynamics became the basis of practical solutions to engineering problems.
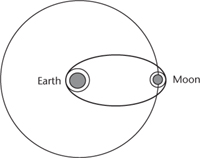
Fig 14
Hohmann transfer ellipse from low-Earth orbit to lunar orbit.
It all started with a simple question: What is the most efficient route from the Earth to the Moon or the planets? The classic answer, known as a Hohmann transfer ellipse (
Figure 14
), starts from a circular orbit round the Earth, and then follows part of a long, thin ellipse to join up with a second circular orbit round the destination. This method was employed for the Apollo missions of the 1960s and 1970s, but for many types of mission it has one disadvantage. The spacecraft must be boosted out of Earth orbit and slowed again to enter lunar orbit; this wastes fuel. There are
alternatives involving many loops round the Earth, a transition through the point between Earth and Moon where their gravitational fields cancel, and many loops round the Moon. But trajectories like that take longer than Hohmann ellipses, so they were not used for the manned Apollo missions where food and oxygen, hence time, were of the essence. For unmanned missions, however, time is relatively cheap, whereas anything that adds to the overall weight of the spacecraft, including fuel, costs money.
By taking a fresh look at Newton's law of gravity and his second law of motion, mathematicians and space engineers have recently discovered a new, and remarkable, approach to fuel-efficient interplanetary travel.
Go by tube.
It's an idea straight out of science fiction. In his 2004
Pandora's Star
, Peter Hamilton portrays a future where people travel to planets encircling distant stars by train, running the railway lines through a wormhole, a short cut through space-time. In his Lensman series from 1934 to 1948, Edward Elmer âDoc' Smith came up with the hyperspatial tube, which malevolent aliens used to invade human worlds from the fourth dimension.
Although we don't yet have wormholes or aliens from the fourth dimension, it has been discovered that the planets and moons of the Solar System are tied together by a network of tubes, whose mathematical definition requires many more dimensions than four. The tubes provide energy-efficient routes from one world to another. They can be seen only through mathematical eyes, because they are not made of matter: their walls are energy levels. If we could visualise the ever-changing landscape of gravitational fields that controls how the planets move, we would be able to see the tubes, swirling along with the planets as they orbit the Sun.
Tubes explain some puzzling orbital dynamics. Consider, for example, the comet called Oterma. A century ago, Oterma's orbit was well outside that of Jupiter. But after a close encounter with the giant planet, the comet's orbit shifted inside that of Jupiter. After another close encounter, it switched back outside again. We can confidently predict that Oterma will continue to switch orbits in this way every few decades: not because it breaks Newton's law, but because it obeys it.
This is a far cry from tidy ellipses. The orbits predicted by Newtonian gravity are elliptical only when no other bodies exert a significant gravitational pull. But the Solar System is full of other bodies, and they can make a huge â and surprising â difference. It is here that the tubes enter the story. Oterma's orbit lies inside two tubes, which meet near Jupiter. One tube lies inside Jupiter's orbit, the other outside. They enclose special
orbits in 3 : 2 and 2 : 3 resonance with Jupiter, meaning that a body in such an orbit will go round the Sun three times for every two revolutions of Jupiter, or two times for every three. At the tube junction near Jupiter, the comet can switch tubes, or not, depending on rather subtle effects of Jovian and solar gravity. But once inside a tube, Oterma is stuck there until the tube returns to the junction. Like a train that has to stay on the rails, but can change its route to another set of rails if someone switches the points, Oterma has some freedom to change its itinerary, but not a lot (
Figure 15
).
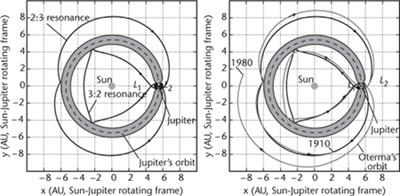
Fig 15
Left
: Two periodic orbits, in 2 : 3 and 3 : 2 resonance with Jupiter, connected via Lagrange points.
right
: Actual orbit of comet Oterma, 1910â1980.
The tubes and their junctions may seem bizarre, but they are natural and important features of the gravitational geography of the Solar System. Victorian railway-builders understood the need to exploit natural features of the landscape, running railways through valleys and along contour lines, and digging tunnels through hills rather than taking the train over the top. One reason was that trains tend to slip on steep gradients, but the main one was energy. Climbing a hill, against the force of gravity, costs energy, which shows up as increased fuel consumption, which costs money.
It's much the same with interplanetary travel. Imagine a spacecraft moving through space. Where it goes next does not depend solely on where it is now: it also depends on how fast it is moving and in which direction. It takes three numbers to specify the spacecraft's position â for example its direction from the Earth, which requires two numbers (astronomers use right ascension and declination, which are analogous to longitude and
latitude on the celestial sphere, the apparent sphere formed by the night sky), and its distance from the Earth. It takes a further three numbers to specify its velocity in those three directions. So the spacecraft travels through a mathematical landscape that has six dimensions rather than two.
A natural landscape is not flat: it has hills and valleys. It takes energy to climb a hill, but a train can gain energy by rolling down into a valley. In fact, two types of energy come into play. The height above sea-level determines the train's potential energy, which represents work done against the force of gravity. The higher you go, the more potential energy you must create. The second kind is kinetic energy, which corresponds to speed. The faster you go, the greater your kinetic energy becomes. When the train rolls downhill and accelerates, it trades potential energy for kinetic. When it climbs a hill and slows down, the trade is in the reverse direction. The total energy is constant, so the train's trajectory is analogous to a contour line in the energy landscape. However, trains have a third source of energy: coal, diesel, or electricity. By expending fuel, a train can climb a gradient or speed up, freeing itself from its natural free-running trajectory. The total energy still cannot change, but all else is negotiable.
