In Pursuit of the Unknown (53 page)

•
H
is a continuous function of
p
₁
,
p
₂
, . . .,
p
_n
. That is, small changes in the probabilities should lead to small changes in the amount of information.

•
If all of the probabilities are equal, which implies they are all 1/n, then
H
should increase if
n
gets larger. That is, if you are choosing between 3 symbols, all equally likely, then the information you receive should be more than if the choice were between just 2 equally likely symbols; a choice between 4 symbols should convey more information than a choice between 3 symbols, and so on.

•
If there is a natural way to break a choice down into two successive
choices, then the original
H
should be a simple combination of the new
H
s.

This final condition is most easily understood using an example, and I've put one in the Notes.
¹
Shannon proved that the
only
function
H
that obeys his three principles is

H
(
p
₁
,
p
₂
, . . .,
p
_n
) = −
p
₁
log
p
₁
−
p
₂
log
p
₂
− . . . −
p
_n
log
p
_n

or a constant multiple of this expression, which basically just changes the unit of information, like changing from feet to metres.

There is a good reason to take the constant to be 1, and I'll illustrate it in one simple case. Think of the four binary strings 00, 01, 10, 11 as symbols in their own right. If 0 and 1 are equally likely, each string has the same probability, namely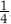
. The amount of information conveyed by one choice a such a string is therefore

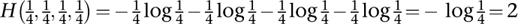
That is, 2 bits. Which is a sensible number for the information in a length-2 binary string when the choices 0 and 1 are equally likely. In the same way, if the symbols are all length-
n
binary strings, and we set the constant to 1, then the information content is
n
bits. Notice that when
n
= 2 we obtain the formula pictured in
Figure 56
. The proof of Shannon's theorem is too complicated to give here, but it shows that if you accept Shannon's three conditions then there is a single natural way to quantify information.
²
The equation itself is merely a definition: what counts is how it performs in practice.

Shannon used his equation to prove that there is a fundamental limit on how much information a communication channel can convey. Suppose that you are transmitting a digital signal along a phone line, whose capacity to carry a message is at most
C
bits per second. This capacity is determined by the number of binary digits that the phone line can transmit, and it is not related to the probabilities of various signals. Suppose that the message is being generated from symbols with information content
H
, also measured in bits per second. Shannon's theorem answers the question: if the channel is noisy, can the signal be encoded so that the proportion of errors is as small as we wish? The answer is that this is always possible, no matter what the noise level is, if
H
is less than or equal to
C
. It is not possible if
H
is greater than
C
. In fact, the proportion of errors cannot be reduced below the difference
H
–
C
, no
matter which code is employed, but there exist codes that get as close as you wish to that error rate.

Shannon's proof of his theorem demonstrates that codes of the required kind exist, in each of his two cases, but the proof doesn't tell us what those codes are. An entire branch of information science, a mixture of mathematics, computing, and electronic engineering, is devoted to finding efficient codes for specific purposes. It is called coding theory. The methods for coming up with these codes are very diverse, drawing on many areas of mathematics. It is these methods that are incorporated into our electronic gadgetry, be it a smartphone or
Voyager 1
's transmitter. People carry significant quantities of sophisticated abstract algebra around in their pockets, in the form of software that implements error-correcting codes for mobile phones.

I'll try to convey the flavour of coding theory without getting too tangled in the complexities. One of the most influential concepts in the theory relates codes to multidimensional geometry. It was published by Richard Hamming in 1950 in a famous paper, ‘Error detecting and error correcting codes'. In its simplest form, it provides a comparison between strings of binary digits. Consider two such strings, say 10011101 and 10110101. Compare corresponding bits, and count how many times they are different, like this:

10
0
1
1
101

10
1
1
0
101

where I've marked the differences in bold type. Here there are two locations at which the bit-strings differ. We call this number the Hamming distance between the two strings. It can be thought of as the smallest number of one-bit errors that can convert one string into the other. So it is closely related to the likely effect of errors, if these occur at a known average rate. That suggests it might provide some insight into how to detect such errors, and maybe even how to put them right.

Multidimensional geometry comes into play because the strings of a fixed length can be associated with the vertices of a multidimensional ‘hypercube'. Riemann taught us how to think of such spaces by thinking of lists of numbers. For example, a space of four dimensions consists of all possible lists of four numbers: (
x
₁
,
x
₂
,
x
₃
,
x
₄
). Each such list is considered to represent a point in the space, and all possible lists can in principle occur.
The separate
xs
are the coordinates of the point. If the space has 157 dimensions, you have to use lists of 157 numbers: (
x
₁
,
x
₂
, . . .,
x
₁₅₇
). It is often useful to specify how far apart two such lists are. In ‘flat' Euclidean geometry this is done using a simple generalisation of Pythagoras's theorem. Suppose we have a second point (
y
₁
,
y
₂
, . . .,
y
₁₅₇
) in our 157-dimensional space. Then the distance between the two points is the square root of the sum of the squares of the differences between corresponding coordinates. That is,

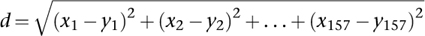
If the space is curved, Riemann's idea of a metric can be used instead.

Hamming's idea is to do something very similar, but the values of the coordinates are restricted to just 0 and 1. Then (
x
₁
−
y
₁
)
²
is 0 if
x
₁
and
y
₁
are the same, but 1 if not, and the same goes for (
x
₂
−
y
₂
)
²
and so on. He also omitted the square root, which changes the answer, but in compensation the result is always a whole number, equal to the Hamming distance. This notion has all the properties that make ‘distance' useful, such as being zero only when the two strings are identical, and ensuring that the length of any side of a ‘triangle' (a set of three strings) is less than or equal to the sum of the lengths of the other two sides.

We can draw pictures of all bit strings of lengths 2, 3, and 4 (and with more effort and less clarity, 5, 6, and possibly even 10, though no one would find that useful). The resulting diagrams are shown in
Figure 57
.

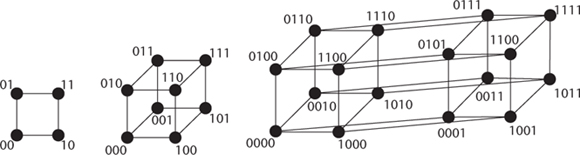
Fig 57
Spaces of all bit-strings of lengths 2, 3, and 4.

The first two are recognisable as a square and a cube (projected on to a plane because it has to be printed on a sheet of paper). The third is a hypercube, the 4-dimensional analogue, and again this has to be projected on to a plane. The straight lines joining the dots have Hamming length 1 – the two strings at either end differ in precisely one location, one
coordinate. The Hamming distance between any two strings is the number of such lines in the shortest path that connects them.

Suppose we are thinking of 3-bit strings, living on the corners of a cube. Pick one of the strings, say 101. Suppose the rate of errors is at most one bit in every three. Then this string may either be transmitted unchanged, or it could end up as any of 001, 111, or 100. Each of these differs from the original string in just one location, so its Hamming distance from the original string is 1. In a loose geometrical image, the erroneous strings lie on a ‘sphere' centred at the correct string, of radius 1. The sphere consists of just three points, and if we were working in 157-dimensional space with a radius of 5, say, it wouldn't even look terribly spherical. But it plays a similar role to an ordinary sphere: it has a fairly compact shape, and it contains exactly the points whose distance from the centre is less than or equal to the radius.

Suppose we use the spheres to construct a code, so that each sphere corresponds to a new symbol, and that symbol is encoded with the coordinates of the centre of the sphere. Suppose moreover that these spheres don't overlap. For instance, I might introduce a symbol
a
for the sphere centred at 101. This sphere contains four strings: 101, 001, 111, and 100. If I receive any of these four strings, I know that the symbol was originally
a
. At least, that's true provided my other symbols correspond in a similar way to spheres that do not have any points in common with this one.