In Pursuit of the Unknown (19 page)

f
(
z
) =
u
(
z
) + i
v
(
z
)

Now you have two
real
-valued functions
u
and
v
, defined for any
z
in the complex plane. Moreover, whatever function you start with, these two component functions satisfy differential equations found in physics. In a fluid-flow interpretation, for example,
u
and
v
determine the flow-lines. In an electrostatic interpretation, the two components determine the electric field and how a small charged particle would move; in a magnetic interpretation, they determine the magnetic field and the lines of force.

I'll give just one example: a bar magnet. Most of us remember seeing a famous experiment in which a magnet is placed beneath a sheet of paper, and iron filings are scattered over the paper. They automatically line up to show the lines of magnetic force associated with the magnet – the paths that a tiny test magnet would follow if placed in the magnetic field. The curves look like
Figure 19
(
left
).

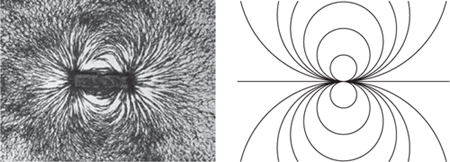
Fig 19
Left
: Magnetic field of bar magnet.
right
: Field derived using complex analysis.

To obtain this picture using complex functions, we just let
f
(
z
) = 1/
z
. The lines of force turn out to be circles, tangent to the real axis, as in Figure
19 (
right
). This is what the magnetic fields lines of a very tiny bar magnet would look like. A more complicated choice of function corresponds to a magnet of finite size: I chose this function to keep everything as simple as possible.

This was wonderful. There were endless functions to work with. You decided which function to look at, found its real and imaginary parts, worked out their geometry . . . and, lo and behold, you had solved a problem in magnetism, or electricity, or fluid flow. Experience soon told you which function to use for which problem. The logarithm was a point source, minus the logarithm was a sink through which fluid disappeared like the plughole in a kitchen sink, i times the logarithm was a point vortex where the fluid spun round and round. . . It was magic! Here was a method that could churn out solution after solution to problems that would otherwise be opaque. Yet it came with a guarantee of success, and if you were worried about all that complex analysis stuff, you could check directly that the results you obtained really did represent solutions.

This was just the beginning. As well as special solutions, you could prove general principles, hidden patterns in the physical laws. You could analyse waves and solve differential equations. You could transform shapes into other shapes, using complex equations, and the same equations transformed the flow-lines round them. The method was limited to systems in the plane, because that was where a complex number naturally lived, but the method was a godsend when previously even problems in the plane were out of reach. Today, every engineer is taught how to use complex analysis to solve practical problems, early in their university course. The Joukowski transformation
z
+ 1/
z
turns a circle into an aerofoil shape, the cross-section of a rudimentary aeroplane wing, see
Figure 20
. It therefore turns the flow past a circle, easy to find if you knew the tricks of the trade, into the flow past an aerofoil. This calculation, and more realistic improvements, were important in the early days of aerodynamics and aircraft design.

This wealth of practical experience made the foundational issues moot. Why look a gift horse in the mouth? There had to be a sensible meaning for complex numbers – they wouldn't work otherwise. Most scientists and mathematicians were much more interested in digging out the gold than they were in establishing exactly where it had come from and what distinguished it from fools' gold. But a few persisted. Eventually, the Irish mathematician William Rowan Hamilton knocked the whole thing on the
head. He took the geometric representation proposed by Wessel, Argand, and Gauss, and expressed it in coordinates. A complex number was a pair of real numbers (
x
,
y
). The real numbers were those of the form (
x
, 0). The imaginary i was (0, 1). There were simple formulas for adding and multiplying these pairs. If you were worried about some law of algebra, such as the commutative law
ab
=
ba
, you could routinely work out both sides as pairs, and make sure they were the same. (They were.) If you identified (
x
, 0) with plain
x
, you embedded the real numbers into the complex ones. Better still,
x
+ i
y
then worked out as the pair (
x
,
y
).

Fig 20
Flow past a wing derived from the Joukowski transformation.

This wasn't just a representation, but a
definition
. A complex number, said Hamilton, is nothing more nor less than a pair of ordinary real numbers. What made them so useful was an inspired choice of the rules for adding and multiplying them. What they actually were was trite; it was how you used them that produced the magic. With this simple stroke of genius, Hamilton cut through centuries of heated argument and philosophical debate. But by then, mathematicians had become so used to working with complex numbers and functions that no one cared any more. All you needed to remember was that i
²
= –1.

 

 

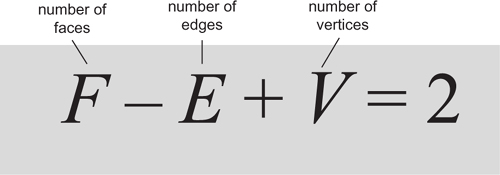
The numbers of faces, edges, and vertices of a solid are not independent, but are related in a simple manner.

It distinguishes between solids with different topologies using the earliest example of a topological invariant. This paved the way to more general and more powerful techniques, creating a new branch of mathematics.

One of the most important and powerful areas of pure mathematics: topology, which studies geometric properties that are unchanged by continuous deformations. Examples include surfaces, knots, and links. Most applications are indirect, but its influence behind the scenes is vital. It helps us understand how enzymes act on DNA in a cell, and why the motion of celestial bodies can be chaotic.

A
s the nineteenth century approached its end, mathematicians began to develop a new kind of geometry, one in which familiar concepts such as lengths and angles played no role whatsoever and no distinction was made between triangles, squares, and circles. Initially it was called
analysis situs
, the analysis of position, but mathematicians quickly settled on another name: topology.

Topology has its roots in a curious numerical pattern that Descartes noticed in 1639 when thinking about Euclid's five regular solids. Descartes was a French-born polymath who spent most of his life in the Dutch Republic, present-day Netherlands. His fame mainly rests on his philosophy, which proved so influential that for a long time Western philosophy consisted largely of responses to Descartes. Not always in agreement, you appreciate, but motivated by his arguments nonetheless. His sound bite
cogito ergo sum
– ‘I think, therefore I am' – has become common cultural currency. But Descartes's interests extended beyond philosophy into science and mathematics.

In 1639 Descartes turned his attention to the regular solids, and this was when he noticed his curious numerical pattern. A cube has 6 faces, 12 edges, and 8 vertices; the sum 6–12+8 equals 2. A dodecahedron has 12 faces, 30 edges, and 20 vertices; the sum 12–30+20=2. An icosahedron has 20 faces, 30 edges, and 12 vertices; the sum 20–30+12=2. The same relationship holds for the tetrahedron and octahedron. In fact, it applies to a solid of
any
shape, regular or not. If the solid has
F
faces,
E
edges, and
V
vertices, then
F
–
E
+
V
=2. Descartes viewed this formula as a minor curiosity and did not publish it. Only much later did mathematicians see this simple little equation as one of the first tentative steps towards the great success story in twentieth-century mathematics, the inexorable rise of topology. In the nineteenth century, the three pillars of pure mathematics were algebra, analysis, and geometry. By the end of the twentieth, they were algebra, analysis, and topology.

Topology is often characterised as ‘rubber-sheet geometry' because it is the kind of geometry that would be appropriate for figures drawn on a sheet of elastic, so that lines can bend, shrink, or stretch, and circles can be squashed so that they turn into triangles or squares. All that matters is
continuity
: you are not allowed to rip the sheet apart. It may seem remarkable that anything so weird could have any importance, but continuity is a basic aspect of the natural world and a fundamental feature of mathematics. Today we mostly use topology indirectly, as one mathematical technique among many. You don't find anything obviously topological in your kitchen. However, a Japanese company did market a chaotic dishwasher, which according to their marketing people cleaned dishes more efficiently, and our understanding of chaos rests on topology. So do some important aspects of quantum field theory and that iconic molecule DNA. But, when Descartes counted the most obvious features of the regular solids and noticed that they were not independent, all this was far in the future.

It was left to the indefatigable Euler, the most prolific mathematician in history, to prove and publish this relationship, which he did in 1750 and 1751. I'll sketch a modern version. The expression
F
–
E
+
V
may seem fairly arbitrary, but it has a very interesting structure. Faces (
F
) are polygons, of dimension 2, edges (
E
) are lines, so have dimension 1, and vertices (
V
) are points, of dimension 0. The signs in the expression alternate, +–+, with + being assigned to features of even dimension and – to those of odd dimension. This implies that you can simplify a solid by merging its faces or removing edges and vertices, and these changes will not alter the number
F
–
E
+
V
provided that every time you get rid of a face you also remove an edge, or every time you get rid of a vertex you also remove an edge. The alternating signs mean that changes of this kind cancel out.