In Pursuit of the Unknown (18 page)

Leibniz had no doubt about the importance of imaginary numbers. In 1702 he wrote: ‘The Divine Spirit found a sublime outlet in that wonder of analysis, that portent of the ideal world, that amphibian between being and non-being, which we call the imaginary root of negative unity.' But the eloquence of his statement fails to obscure a fundamental problem: he didn't have a clue what imaginary numbers actually were.

One of the first people to come up with a sensible representation of complex numbers was Wallis. The image of real numbers lying along a line, like marked points on a ruler, was already commonplace. In 1673 Wallis suggested that a complex number
x
+ i
y
should be thought of as a point in a plane. Draw a line in the plane, and identify points on this line with real numbers in the usual way. Then think of
x
+ i
y
as a point lying to one side of the line, distance
y
away from the point
x
.

Wallis's idea was largely ignored, or worse, criticised. François Daviet de Foncenex, writing about imaginaries in 1758, said that thinking of imaginaries as forming a line at right angles to the real line was pointless. But eventually the idea was revived in a slightly more explicit form. In fact, three people came up with exactly the same method for representing complex numbers, at intervals of a few years,
Figure 18
. One was a Norwegian surveyor, one a French mathematician, and one a German mathematician. Respectively, they were Caspar Wessel, who published in 1797, Jean-Robert Argand in 1806, and Gauss in 1811. They basically said the same as Wallis, but they added a second line to the picture, an
imaginary axis at right angles to the real one. Along this second axis lived the imaginary numbers i, 2i, 3i, and so on. A general complex number, such as 3 + 2i, lived out in the plane, three units along the real axis and two along the imaginary one.

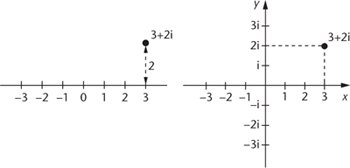
Fig 18
The complex plane.
Left
: according to Wallis.
right
: according to Wessel, Argand, and Gauss.

This geometric representation was all very well, but it didn't explain why complex numbers form a logically consistent system. It didn't tell us in what sense they are
numbers
. It just provided a way to visualise them. This no more defined what a complex number
is
than a drawing of a straight line defines a real number. It did provide some sort of psychological prop, a slightly artificial link between those crazy imaginaries and the real world, but nothing more.

What convinced mathematicians that they should take imaginary numbers seriously wasn't a logical description of what they were. It was overwhelming evidence that whatever they were, mathematics could make good use of them. You don't ask difficult questions about the philosophical basis of an idea when you are using it every day to solve problems and you can see that it gives the right answers. Foundational questions still have some interest, of course, but they take a back seat to the pragmatic issues of using the new idea to solve old and new problems.

Imaginary numbers, and the system of complex numbers that they spawned, cemented their place in mathematics when a few pioneers turned their attention to complex analysis: calculus (
Chapter 3
) but with complex numbers instead of real ones. The first step was to extend all the usual functions – powers, logarithms, exponentials, trigonometric
functions – to the complex realm. What is sin
z
when
z
=
x
+ i
y
is complex? What is e
^z
or log
z
?

Logically, these things can be whatever we wish. We are operating in a new domain where the old ideas don't apply. It doesn't make much sense, for instance, to think of a right-angled triangle whose sides have complex lengths, so the geometric definition of the sine function is irrelevant. We could take a deep breath, insist that sin
z
has its usual value when
z
is real, but equals 42 whenever
z
isn't real: job done. But that would be a pretty silly definition: not because it's imprecise, but because it bears no sensible relationship to the original one for real numbers. One requirement for an extended definition must be that it agrees with the old one when applied to real numbers, but that's not enough. It's true for my silly extension of the sine. Another requirement is that the new concept should retain as many features of the old one as we can manage; it should somehow be ‘natural'.

What properties of sine and cosine do we want to preserve? Presumably we'd like all the pretty formulas of trigonometry to remain valid, such as sin 2
z
= 2 sin
z
cos
z
. This imposes a constraint but doesn't help. A more interesting property, derived using analysis (the rigorous formulation of calculus), is the existence of an infinite series:

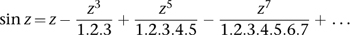
(The sum of such a series is defined to be the limit of the sum of finitely many terms as the number of terms increases indefinitely.) There is a similar series for the cosine:

and the two are obviously related in some way to the series for the exponential:

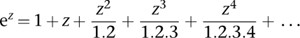
These series may seem complicated, but they have an attractive feature: we know how to make sense of them for complex numbers. All they involve is integer powers (which we obtain by repeated multiplication) and a technical issue of convergence (making sense of the infinite sum). Both of these extend naturally into the complex realm and have all of the
expected properties. So we can define sines and cosines of complex numbers using the same series that work in the real case.

Since all of the usual formulas in trigonometry are consequences of these series, those formulas automatically carry over as well. So do the basic facts of calculus, such as ‘the derivative of sine is cosine'. So does e
^z+w
= e
^z
e
^w
. This is all so pleasant that mathematicians were happy to settle on the series definitions. And once they'd done that, a great deal else necessarily had to fit in with it. If you followed your nose, you could discover where it led.

For example, those three series look very similar. Indeed, if you replace
z
by iz in the series for the exponential, you can split the resulting series into two parts, and what you get are precisely the series for sine and cosine. So the series definitions imply that

e
^iz
= cos
z
+ i sin
z
.

You can also express both sine and cosine using exponentials:

This hidden relationship is extraordinarily beautiful. But you'd never suspect anything like it could exist if you remained stuck in the realm of the reals. Curious similarities between trigonometric formulas and exponential ones (for example, their infinite series) would remain just that. Viewed through complex spectacles, everything suddenly slots into place.

One of the most beautiful, yet enigmatic, equations in the whole of mathematics emerges almost by accident. In the trigonometric series, the number
z
(when real) has to be measured in radians, for which a full circle of 360° becomes 2π radians. In particular, the angle 180° is π radians. Moreover, sin π = 0 and cos π = –1. Therefore

e
^iπ
= cos π + i sin π = –1

The imaginary number i unites the two most remarkable numbers in mathematics, e and π, in a single elegant equation. If you've never seen this before, and have any mathematical sensitivity, the hairs on your neck raise and prickles run down your spine. This equation, attributed to Euler, regularly comes top of the list in polls for the most beautiful equation in mathematics. That doesn't mean that it
is
the most beautiful equation, but it does show how much mathematicians appreciate it.

Armed with complex functions and knowing their properties, the mathematicians of the nineteenth century discovered something remarkable: they could use these things to solve differential equations in mathematical physics. They could apply the method to static electricity, magnetism, and fluid flow. Not only that: it was
easy
.

In
Chapter 3
we talked of functions – mathematical rules that assign, to any given number, a corresponding number, such as its square or sine. Complex functions are defined in the same way, but now we allow the numbers involved to be complex. The method for solving differential equations was delightfully simple. All you had to do was take some complex function, call it
f
(
z
), and split it into its real and imaginary parts: