Gödel, Escher, Bach: An Eternal Golden Braid (28 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

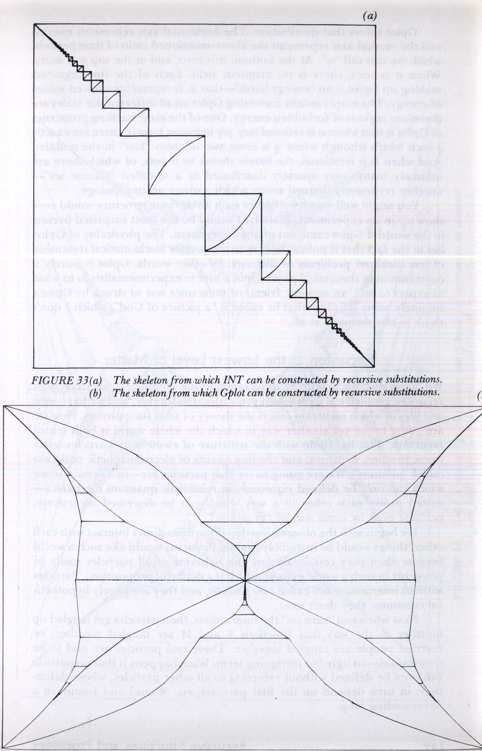
To see this even more dramatically, imagine keeping the recursive part of the definition of
INT
, but changing the initial picture, the skeleton. A variant skeleton is shown in Figure 33b, again with boxes which get smaller and smaller as they trail off to the four corners. If you nest this second skeleton inside itself over and over again, you will create the key graph from my Ph.D. thesis, which I call
Gplot
(Fig. 34). (In fact, some complicated distortion of each copy is needed as well-but nesting is the basic idea.).
Gplot is thus a member of the
INT
-family. It is a distant relative, because its skeleton is quite different from-and considerably more complex than-that of INT.
However, the recursive part of the definition is identical, and therein lies the family tie.
I should not keep you too much in the dark about the origin of these beautiful graphs.
INT-standing for "interchange"-comes from a problem involving "Eta-sequences", which are related to continued fractions. The basic idea behind
INT
is that plus and minus signs are interchanged in a certain kind of continued fraction. As a consequence,
INT(INT
(x))
= x.
INT
has the property that if x is rational, so is
INT
(x); if x is quadratic, so is
INT
(x).
I do not know if this trend holds for higher algebraic degrees. Another lovely feature of
INT
is that at all rational values of x, it has a jump discontinuity, but at all irrational values of x, it is continuous.
Gplot comes from a highly idealized version of the question, "What are the allowed energies of electrons in a crystal in a magnetic field?" This problem is interesting because it is a cross between two very simple and fundamental physical situations: an electron in a perfect crystal, and an electron in a homogeneous magnetic field. These two simpler problems are both well understood, and their characteristic solutions seem almost incompatible with each other. Therefore, it is of quite some interest to see how nature manages to reconcile the two. As it happens, the crystal without-magnetic-field situation and the magnetic-field-without-crystal situation do have one feature in common: in each of them, the electron behaves periodically in time. It turns out that when the two situations are combined, the ratio of their two time periods is the key parameter. In fact, that ratio holds all the information about the distribution of allowed electron energies-but it only gives up its secret upon being expanded into a continued fraction.
Gplot shows that distribution. The horizontal axis represents energy, and the vertical axis represents the above-mentioned ratio of time periods, which we can call "α".
At the bottom, a is zero, and at the top a is unity. When a is zero, there is no magnetic field. Each of the line segments making up Gplot is an "energy band"-that is, it represents allowed values of energy. The empty swaths traversing Gplot on all different size scales are therefore regions of forbidden energy. One of the most startling properties of Gplot is that when a is rational (say
p/q
in lowest terms), there are exactly
q
such bands (though when
q
is even, two of them "kiss" in the middle). And when
a
is irrational, the bands shrink to points, of which there are infinitely many, very sparsely distributed in a so-called "Cantor set" -- another recursively defined entity which springs up in topology.
You might well wonder whether such an intricate structure would ever show up in an experiment. Frankly, I would be the most surprised person in the world if Gplot came out of any experiment. The physicality of Gplot lies in the fact that it points the way to the proper mathematical treatment of less idealized problems of this sort. In other words, Gplot is purely a contribution to theoretical physics, not a hint to experimentalists as to what to expect to see! An agnostic friend of mine once was so struck by Gplot's infinitely many infinities that he called it "a picture of God", which I don't think is blasphemous at all.
Recursion at the Lowest Level of Matter
We have seen recursion in the grammars of languages, we have seen recursive geometrical trees which grow upwards forever, and we have seen one way in which recursion enters the theory of solid state physics. Now we are going to see yet another way in which the whole world is built out of recursion. This has to do with the structure of elementary particles: electrons, protons, neutrons, and the tiny quanta of electromagnetic radiation called "photons". We are going to see that particles are-in a certain sense which can only be defined rigorously in relativistic quantum mechanics --
nested inside each other in a way which can be described recursively, perhaps even by some sort of "grammar".
We begin with the observation that if particles didn't interact with each other, things would be incredibly simple. Physicists would like such a world because then they could calculate the behavior of all particles easily (if physicists in such a world existed, which is a doubtful proposition). Particles without interactions are called
bare particles
, and they are purely hypothetical creations; they don't exist.
Now when you "turn on" the interactions, then particles get tangled up together in the way that functions F and M are tangled together, or married people are tangled together. These real particles are said to be
renormalized
-an ugly but intriguing term.
What happens is that no particle can even be defined without referring to all other particles, whose definitions in turn depend on the first particles, etc. Round and round, in a never-ending loop.
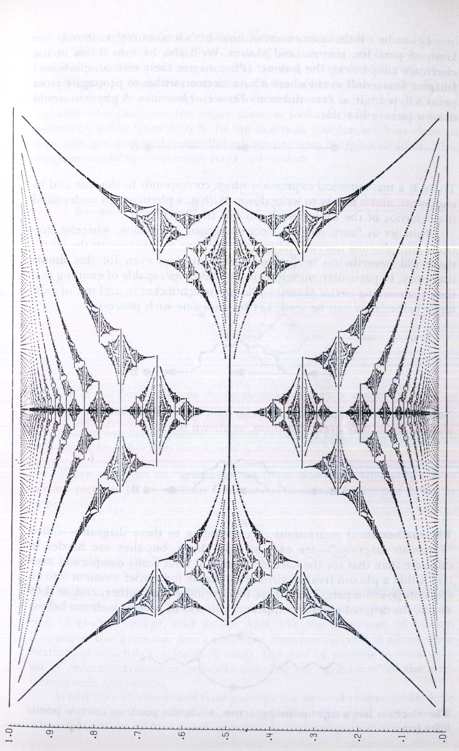
Figure 34. Gplot; a recursive graph, showing energy bands for electrons in an idealized
crystal in a magnetic field,
α
representing magnetic field strength, runs vertically from 0
to 1. Energy runs horizontally. The horizontal line segments are bands of allowed
electron energies.


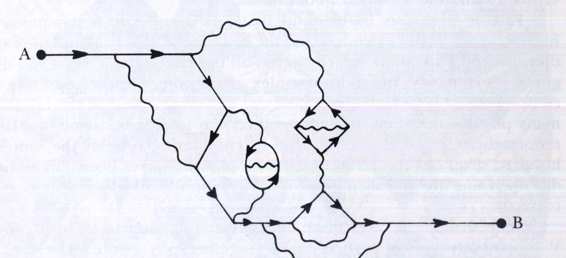
Let us be a little more concrete, now. Let's limit ourselves to only two kinds of particles:
electrons
and
photons
. We'll also have to throw in the electron's antiparticle, the
positron
. (Photons are their own antiparticles.) Imagine first a dull world where a bare electron wishes to propagate from point A to point B, as Zeno did in my
Three-Part
Invention.
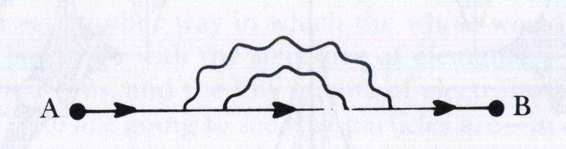
A physicist would draw a picture like this:
There is a mathematical expression which corresponds to this line and its endpoints, and it is easy to write down. With it, a physicist can understand the behavior of the bare electron in this trajectory.
Now let us "turn on" the electromagnetic interaction, whereby electrons and photons interact. Although there are no photons in the scene, there will nevertheless be profound consequences even for this simple trajectory. In particular, our electron now becomes capable of emitting and then reabsorbing
virtual photons
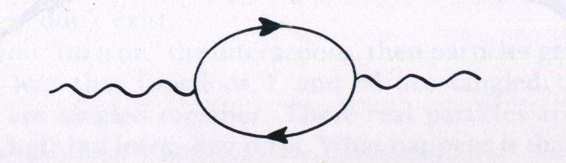
-photons which flicker in and out of existence before they can be seen. Let us show one such process: Now as our electron propagates, it may emit and reabsorb one photon after another, or it may even nest them, as shown below:
The mathematical expressions corresponding to these diagrams-called "Feynman diagrams"-are easy to write down, but they are harder to calculate than that for the bare electron. But what really complicates matters is that a photon (real or virtual) can decay for a brief moment into an electron-positron pair. Then these two annihilate each other, and, as if by magic, the original photon reappears. This sort of process is shown below: The electron has a right-pointing arrow, while the positron's arrow points leftwards.