Gödel, Escher, Bach: An Eternal Golden Braid (25 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

(Suddenly, a giant, booming laugh is heard, alarmingly close to
them.)
Tortoise: Watch out, Achilles! This is no laughing matter.
Majotaur: Hee hee hee! Ho ho! Haw haw haw!
Achilles: I'm starting to feel weak, Mr. T ...
Tortoise: Try to pay no attention to his laugh,
Achilles. That's your only hope.
Achilles: I'll do my best. If only my stomach weren't empty!
Tortoise: Say, am I smelling things, or is there a bowl of hot buttered popcorn around here? Achilles: I smell it, too. Where is it coming from?
Tortoise: Over here, I think. Oh! I just ran into a big bowl of the stuff.
Yes, indeed-it seems to be a bowl of popcorn!
Achilles: Oh, boy-popcorn! I'm going to munch my head off!
Tortoise: Let's just hope it isn't pushcorn! Pushcorn and popcorn are extraordinarily difficult to tell apart.
Achilles: What's this about Pushkin?
Tortoise: I didn't say a thing. You must be hearing things.
Achilles: Go-golly! I hope not. Well, let's dig in!
(And the two Jriends begin muncnai popcorn (or pushcorn?)-and t
once POP! I guess it was popcorn; all.)
Tortoise: What an amusing story. Did you en
Achilles: Mildly. Only I wonder whether the' out of that Evil Majotaur's pit or r Achilles-he wanted to be full-sized again
Tortoise: Don't worry-they're out, and he is again. That's what the "POP"
was all abo
Achilles: Oh, I couldn't tell. Well, now I REAL: find that bottle of tonic.
For some reason, burning. And nothing would taste bett drink of
popping-tonic.
Tortoise: That stuff is renowned for its thirst powers. Why, in some places people very crazy over it. At the turn of the century the Schonberg food factory stopped ma] and started making cereal instead. You cai the uproar that caused.
Achilles: I have an inkling. But let's go look fo Hey just a moment.
Those lizards on the you see anything funny about them?
Tortoise: Umm ... not particularly. What do you see of such great interest?
Achilles: Don't you see it? They're emerging flat picture without drinking any pop] How are they able to do that?
Tortoise: Oh, didn't I tell you? You can ge picture by moving perpendicularly to it you have no popping-tonic. The little li learned to climb UP when they want to ge two-dimensional sketchbook world.
Achilles: Could we do the same thing to get Escher picture we're in?
Tortoise: Of course! We just need to go UP one story. you want to try it?
Achilles: Anything to get back to my house! I all these provocative adventures.
Tortoise: Follow me, then, up this way.
(And they go up one story.)
Achilles: It's good to be back. But something seems wrong. This isn't my house! This is YOUR house, Mr. Tortoise
Tortoise: Well, so it is-and am I glad for that! I wasn’t looking forward one whit to the long walk back from your house. I am bushed, and doubt if I could have made it.
Achilles: I don't mind walking home, so I guess it's lucky we ended up here, after all.
Tortoise: I'll say! This certainly is a piece of Good Fortune!
Recursive Structures
and Processes
What Is Recursion?
WHAT IS RECURSION? It is what was illustrated in the Dialogue
Little Harmonic
Labyrinth
: nesting, and variations on nesting. The concept is very general. (Stories inside stories, movies inside movies, paintings inside paintings, Russian dolls inside Russian dolls (even parenthetical comments in. side parenthetical comments!)-these are just a few of the charms of recursion.) However, you should he aware that the meaning of
"recursive' in this Chapter is only faintly related to its meaning in Chapter 111. The relation should be clear by the end of this Chapter.
Sometimes recursion seems to brush paradox very closely. For example, there are
recursive definitions
. Such a definition may give the casual viewer the impression that something is being defined in terms of
itself.
That would be circular and lead to infinite regress, if not to paradox proper. Actually, a recursive definition (when properly formulated) never leads to infinite regress or paradox. This is because a recursive definition never defines something in terms of itself, but always in terms of
simpler
versions
of itself. What I mean by this will become clearer shortly, when ' show some examples of recursive definitions.
One of the most common ways in which recursion appears in daily life is when you postpone completing a task in favor of a simpler task, often o the same type. Here is a good example. An executive has a fancy telephone and receives many calls on it. He is talking to A when B calls. To A he say,, "Would you mind holding for a moment?" Of course he doesn't really car if A minds; he just pushes a button, and switches to B. Now C
calls. The same deferment happens to B. This could go on indefinitely, but let us not get too bogged down in our enthusiasm. So let's say the call with C terminates. Then our executive "pops" back up to B, and continues. Meanwhile A is sitting at the other end of the line, drumming his fingernails again some table, and listening to some horrible Muzak piped through the phone lines to placate him ... Now the easiest case is if the call with B simply terminates, and the executive returns to A finally. But it
could
happen that after the conversation with B is resumed, a new caller-D-calls. B is once again pushed onto the stack of waiting callers, and D is taken care of. Aft D is done, back to B, then back to A. This executive is hopelessly mechanical, to be sure-but we are illustrating recursion in its most precise form
Pushing, Popping, and Stacks
In the preceding example, I have introduced some basic terminology of recursion-at least as seen through the eyes of computer scientists. The terms are
push, pop
, and
stack
(or
push-down stack
, to be precise) and they are all related. They were introduced in the late 1950's as part of IPL, one of the first languages for Artificial Intelligence. You have already encountered "push" and "pop" in the Dialogue. But I will spell things out anyway. To
push
means to suspend operations on the task you're currently working on, without forgetting where you are-and to take up a new task. The new task is usually said to be "on a lower level" than the earlier task. To
pop
is the reverse-it means to close operations on one level, and to resume operations exactly where you left off, one level higher.
But how do you remember exactly where you were on each different level? The answer is, you store the relevant information in a
stack
. So a stack is just a table telling you such things as (1) where you were in each unfinished task (jargon: the "return address"), (2) what the relevant facts to know were at the points of interruption (jargon: the "variable bindings"). When you pop back up to resume some task, it is the stack which restores your context, so you don't feel lost. In the telephone-call example, the stack tells you who is waiting on each different level, and
where
you were in the conversation when it was interrupted.
By the way, the terms "push", "pop", and "stack" all come from the visual image of cafeteria trays in a stack. There is usually some sort of spring underneath which tends to keep the topmost tray at a constant height, more or less. So when you push a tray onto the stack, it sinks a little-and when you remove a tray from the stack, the stack pops up a little.
One more example from daily life. When you listen to a news report on the radio, oftentimes it happens that they switch you to some foreign correspondent. "We now switch you to Sally Swumpley in Peafog, England." Now Sally has got a tape of some local reporter interviewing someone, so after giving a bit of background, she plays it. "I'm Nigel Cadwallader, here on scene just outside of Peafog, where the great robbery took place, and I'm talking with ..." Now you are three levels down. It may turn out that the interviewee also plays a tape of some conversation. It is not too uncommon to go down three levels in real news reports, and surprisingly enough, we scarcely have any awareness of the suspension. It is all kept track of quite easily by our subconscious mind.
Probably the reason it is so easy is that each level is extremely different in flavor from each other level. If they were all similar, we would get confused in no time flat.
An example of a more complex recursion is, of course, our Dialogue. There, Achilles and the Tortoise appeared on all the different levels. Sometimes they were reading a story in which they appeared as characters. That is when your mind may get a little hazy on what's going on, and you have to concentrate carefully to get things straight.
"Let's see, the real Achilles and Tortoise are still up there in Goodfortune's helicopter, but the
secondary
ones are in some Escher picture-and then they found this book and are reading in it, so it's the
tertiary
Achilles and Tortoise who wandering around inside the grooves of the
Little Harmonic Labyrinth
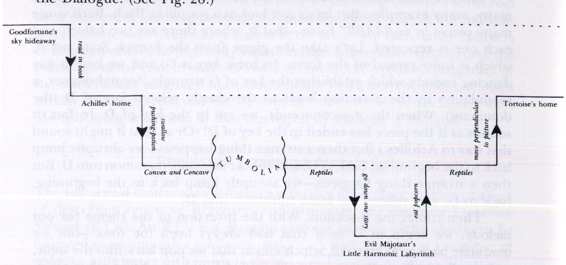
. wait a minute-I left out one level somewhere ..." You have to ha conscious mental stack like this in order to keep track of the recursion the Dialogue. (See Fig. 26.)
FIGURE 26. Diagram of the structure of the Dialogue
Little Harmonic Labyrinth
Vertical descents are "pushes"; rises ore "pops". Notice the similarity of this diagram to
indentation pattern of the Dialogue. From the diagram it is clear that the initial tension
Goodfortune's threat-never was resolved; Achilles and the Tortoise were just left
dangling the sky. Some readers might agonize over this unpopped push, while others
might not ba eyelash. In the story, Bach's musical labyrinth likewise was cut off too soon-but Achilles d even notice anything funny. Only the Tortoise was aware of the more
global dangling tension
Stacks in Music
While we're talking about the Little Harmonic Labyrinth, we should discuss something which is hinted at, if not stated explicitly in the Dialogue: that hear music recursively-in particular, that we maintain a mental stack of keys, and that each new modulation pushes a new key onto the stack. implication is further that we want to hear that sequence of keys retrace reverse order-popping the pushed keys off the stack, one by one, until the tonic is reached. This is an exaggeration. There is a grain of truth to it however.
Any reasonably musical person automatically maintains a shallow with two keys.
In that "short stack", the true tonic key is held and also most immediate "pseudotonic"
(the key the composer is pretending t in). In other words, the most global key and the most local key. That the listener knows when the true tonic is regained, and feels a strong s of "relief". The listener can also distinguish (unlike Achilles) between a
local
easing of tension-for example a resolution into the pseudotonic --
and a
global
resolution. In fact, a pseudoresolution should heighten the global tension, not relieve it, because it is a piece of irony-just like Achilles' rescue from his perilous perch on the swinging lamp, when all the while you know he and the Tortoise are really awaiting their dire fates at the knife of Monsieur Goodfortune.
Since tension and resolution are the heart and soul of music, there are many, many examples. But let us just look at a couple in Bach. Bach wrote many pieces in an
"AABB" form-that is, where there are two halves, and each one is repeated. Let's take the gigue from the French Suite no. 5, which is quite typical of the form. Its tonic key is G, and we hear a gay dancing melody which establishes the key of G strongly. Soon, however, a modulation in the A-section leads to the closely related key of D (the dominant). When the A-section ends, we are in the key of D. In fact, it sounds as if the piece has ended in the key of D! (Or at least it might sound that way to Achilles.) But then a strange thing happens-we abruptly jump back to the beginning, back to G, and rehear the same transition into D. But then a strange thing happens-we abruptly jump back to the beginning, back to G, and rehear the same transition into D.
