Gödel, Escher, Bach: An Eternal Golden Braid (29 page)
Read Gödel, Escher, Bach: An Eternal Golden Braid Online
Authors: Douglas R. Hofstadter
Tags: #Computers, #Art, #Classical, #Symmetry, #Bach; Johann Sebastian, #Individual Artists, #Science, #Science & Technology, #Philosophy, #General, #Metamathematics, #Intelligence (AI) & Semantics, #G'odel; Kurt, #Music, #Logic, #Biography & Autobiography, #Mathematics, #Genres & Styles, #Artificial Intelligence, #Escher; M. C

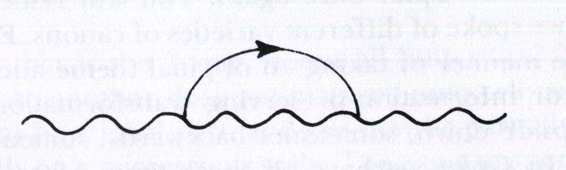
As you might have anticipated, these virtual processes can be inside each other to arbitrary depth. This can give rise to some complicated-looking drawings, such as the one in Figure 35. In that man diagram, a single electron enters on the left at A, does some an acrobatics, and then a single electron emerges on the right at B. outsider who can't see the inner mess, it looks as if one electron peacefully sailed from A to B. In the diagram, you can see how el lines can get arbitrarily embellished, and so can the photon lines diagram would be ferociously hard to calculate.
.
FIGURE 35. A Feynman diagram showing the propagation of a renormalized electron
from A to B. In this diagram, time increases to the right. Therefore, in the segments
where the electron’s arrow points leftwards, it is moving "backwards in time". A more
intuitive way to say this is that an antielectron (positron) is moving forwards in time.
Photons are their own antiparticles; hence their lines have no need of arrows.
There is a sort of "grammar" to these diagrams, that only certain pictures to be realized in nature. For instance, the one be impossible:
You might say it is not a "well-formed" Feynman diagram. The gram a result of basic laws of physics, such as conservation of energy, conservation of electric charge, and so on. And, like the grammars of l - languages, this grammar has a recursive structure, in that it allow' nestings of structures inside each other. It would be possible to drat set of recursive transition networks defining the "grammar" of the electromagnetic interaction.
When bare electrons and bare photons are allowed to interact ii arbitrarily tangled ways, the result is
renormalized
electrons and ph Thus, to understand how a real, physical electron propagates from A to B,
the physicist has to be able to take a sort of average of all the infinitely many different possible drawings which involve virtual particles. This is Zeno with a vengeance!
Thus the point is that a physical particle-a renormalized particle involves (1) a bare particle and (2) a huge tangle of virtual particles, inextricably wound together in a recursive mess. Every real particle's existence therefore involves the existence of infinitely many other particles, contained in a virtual "cloud" which surrounds it as it propagates. And each of the virtual particles in the cloud, of course, also drags along its own virtual cloud, and so on ad infinitum.
Particle physicists have found that this complexity is too much to handle, and in order to understand the behavior of electrons and photons, they use approximations which neglect all but fairly simple Feynman diagrams. Fortunately, the more complex a diagram, the less important its contribution. There is no known way of summing up all of the infinitely many possible diagrams, to get an expression for the behavior of a fully renormalized, physical electron. But by considering roughly the simplest hundred diagrams for certain processes, physicists have been able to predict one value (the so-called g-factor of the muon) to nine decimal places -- correctly!
Renormalization takes place not only among electrons and photons. Whenever any types of particle interact together, physicists use the ideas of renormalization to understand the phenomena. Thus protons and neutrons, neutrinos, pi-mesons, quarks-all the beasts in the subnuclear zoo they all have bare and renormalized versions in physical theories. And from billions of these bubbles within bubbles are all the beasts and baubles of the world composed.
Copies and Sameness
Let us now consider Gplot once again. You will remember that in the Introduction, we spoke of different varieties of canons. Each type of canon exploited some manner of taking an original theme and copying it by an isomorphism, or information-preserving transformation. Sometimes the copies were upside down, sometimes backwards, sometimes shrunken or expanded ... In Gplot we have all those types of transformation, and more. The mappings between the full Gplot and the "copies"
of itself inside itself involve size changes, skewings, reflections, and more. And yet there remains a sort of skeletal identity, which the eye can pick up with a bit of effort, particularly after it has practiced with
INT
.
Escher took the idea of an object's parts being copies of the object itself and made it into a print: his woodcut
Fishes and Scales
(Fig. 36). Of course these fishes and scales are the same only when seen on a sufficiently abstract plane. Now everyone knows that a fish's scales aren't really small copies of the fish; and a fish's cells aren't small copies of the fish; however, a fish's
DNA
, sitting inside each and every one of the fish's cells, is a very convo-

FIGURE 36. Fish and Scales, by M. C. Escher (woodcut, 1959).
luted "copy" of the entire fish-and so there is more than a grain of truth to the Escher picture.
What is there that is the "same" about all butterflies? The mapping from one butterfly to another does not map cell onto cell; rather, it m; functional part onto functional part, and this may be partially on a macroscopic scale, partially on a microscopic scale. The exact proportions of pa are not preserved; just the functional relationships between parts. This is the type of isomorphism which links all butterflies in Escher's wood engraving
Butterflies
(Fig. 37) to each other. The same goes for the more abstract butterflies of Gplot, which are all linked to each other by mathematical mappings that carry functional part onto functional part, but totally ignore exact line proportions, angles, and so on.
Taking this exploration of sameness to a yet higher plane of abstraction, we might well ask, "What is there that is thèsame' about all Esc l drawings?" It would be quite ludicrous to attempt to map them piece by piece onto each other. The amazing thing is that even a tiny section of an

FIGURE 37. Butterflies, by M. C. Escher (wood-engraving, 1950).
Escher drawing or a Bach piece gives it away. Just as a fish's
DNA
is contained inside every tiny bit of the fish, so a creator's "signature" is contained inside every tiny section of his creations. We don't know what to call it but "style" -- a vague and elusive word.
We keep on running up against "sameness-in-differentness", and the question When are two things the same?
It will recur over and over again in this book. We shall come at it from all sorts of skew angles, and in the end, we shall see how deeply this simple question is connected with the nature of intelligence.
That this issue arose in the Chapter on recursion is no accident, for recursion is a domain where "sameness-in-differentness" plays a central role. Recursion is based on the
"same" thing happening on several differ-
ent levels at once. But the events on different levels aren't exactly same-rather, we find some invariant feature in them, despite many s in which they differ. For example, in the
Little Harmonic Labyrinth
, all stories on different levels are quite unrelated-their
"sameness" reside only two facts: (1) they are stories, and (2) they involve the Tortoise and Achilles. Other than that, they are radically different from each other.
Programming and Recursion: Modularity, Loops, Procedures
One of the essential skills in computer programming is to perceive wl two processes are the same in this extended sense, for that leads modularization-the breaking-up of a task into natural subtasks. For stance, one might want a sequence of many similar operations to be cart out one after another. Instead of writing them all out, one can write a h which tells the computer to perform a fixed set of operations and then loop back and perform them again, over and over, until some condition is satisfied. Now the
body
of the loop-the fixed set of instructions to repeated-need not actually be completely fixed. It may vary in so predictable way.
An example is the most simple-minded test for the primality o natural number N, in which you begin by trying to divide N by 2, then 3, 4, 5, etc. until N - 1. If N has survived all these tests without be divisible, it's prime. Notice that each step in the loop is similar to, but i the same as, each other step. Notice also that the number of steps varies with N-hence a loop of fixed length could never work as a general test primality. There are two criteria for "aborting" the loop: (1) if so number divides N exactly, quit with answer "NO"; (2) if N - 1 is react as a test divisor and N survives, quit with answer
"YES".
The general idea of loops, then, is this: perform some series of related steps over and over, and abort the process when specific conditions are n Now sometimes, the maximum number of steps in a loop will be known advance; other times, you just begin, and wait until it is aborted. The second type of loop -- which I call a
free
loop -- is dangerous, because criterion for abortion may never occur, leaving the computer in a socal "infinite loop". This distinction between
bounded loops
and
free loops
is one the most important concepts in all of computer science, and we shall dev an entire Chapter to it:
"BlooP and FlooP and G1ooP".
Now loops may be nested inside each other. For instance, suppose t we wish to test all the numbers between 1 and 5000 for primality. We c write a second loop which uses the above-described test over and over starting with N = I and finishing with N =
5000. So our program i have a "loop-the-loop" structure. Such program structures are typical – in fact they are deemed to be good programming style. This kind of nest loop also occurs in assembly instructions for commonplace items, and such activities as knitting or crocheting-in which very small loops are
repeated several times in larger loops, which in turn are carried out repeatedly ... While the result of a low-level loop might be no more than couple of stitches, the result of a high-level loop might be a substantial portion of a piece of clothing.
In music, too, nested loops often occur-as, for instance, when a scale (a small loop) is played several times in a row, perhaps displaced in pitch each new time. For example, the last movements of both the Prokofiev fifth piano concerto and the Rachmaninoff second symphony contain extended passages in which fast, medium, and slow scale-loops are played simultaneously by different groups of instruments, to great effect. The Prokofiev scales go up; the Rachmaninoff-scales, down. Take your pick.
