A Player's Guide to Chords and Harmony (8 page)

Figure 2-3. The perfect major, and minor intervals. Play these intervals on a keyboard to hear how they sound, and count the number of half-steps within each interval.

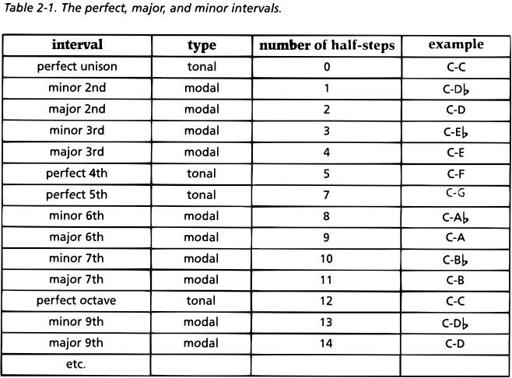
As you look at Table 2-1, you'll notice right away that we've skipped something. What about the interval that consists of six half-steps? Don't worry - it has a name too, but that name requires a little more explanation. We can make tonal perfect intervals larger or smaller by adding or removing a half-step, just as we do with modal intervals. We have to use a different type of name, however. There's no such thing as a "major 5th" or "minor 5th," because the 5th step of the scale is the same whether we're playing in a major or minor mode. Instead, a 5th that has been narrowed by a half-step is called a diminished 5th. A 4th that has been enlarged by a half-step is called an augmented 4th. The interval containing six halfsteps can be referred to either as a diminished 5th or as an augmented 4th, depending on how it's spelled. If the lower note of the interval is C and the upper note is F#, the interval is called an augmented 4th, because the interval C-F contains four scale steps. But if we spell the upper note as a G6, then the interval is called a diminished 5th, because it's looked at as being based on the interval C-G. These intervals are shown in Figure 2-4.

Figure 2-4. Between the perfect 4th and perfect 5th lies the tritone, which can be spelled either as an augmented 4th or a diminished 5th.

An interval that has two names? Isn't that an invitation to confusion? Well, yes, it is. If you look at it a slightly different way, however, the augmented 4th and diminished 5th are really different intervals. They just happen to have the same number of half-steps. To avoid the hassle of figuring out whether they're referring to a diminished 5th or augmented 4th in a particular instance, some people refer to this interval as a tritone. As mentioned in Chapter One, a tritone is an interval that spans three whole-steps.

The number of half-steps in an interval is not the decisive factor in what sort of name we give it. Setting aside oddball terms like "tritone," the factor that determines the name of an interval is, first and foremost, the distance between the letter-names of the two notes that form the interval. As long as the two notes are closer together than an octave, any interval that contains a C as the lower note and an E as the upper note, for instance, or a D as the lower note and an F as the upper note, is always some type of 3rd. Any interval that contains a C as the lower note and a G as the upper note (again, assuming the interval is smaller than an octave) is a 5th. And so on. Naturally, we don't have to use C as the lower note of the interval: An interval whose lower note is a D and whose upper note is an A (assuming they're in the same octave) is a 5th, as is the interval from an E up to a B. This idea is summarized in Figure 2-5.

Figure 2-5. Even though the intervals shown here include accidentals, the name of the interval is still based on the distance between the letter-names of the notes (or, if you prefer, on how many lines and spaces separate the two notes on the staff). The type of interval (major, minor, augmented, or diminished) is based on the number of half-steps. To verify that the names given here are correct, locate these intervals on the keyboard and count the number of half-steps each of them spans.

INTERVALS VS. SCALE STEPS & CHORD MEMBERS

We began by defining intervals in terms of scale steps. The interval between the first and third steps of the scale, for instance, is called a 3rd. It's important to understand that we're using three slightly different but closely related concepts here, which, sad to say, share the same names. Let's look at them one by one:

Within the C major scale, the E is the 3rd scale step, the F is the 4th scale step, and so on. Most of the discussion of scales and scale steps in this book is found in Chapter Seven.

Within a given chord, as explained in Chapter Three, each note has some relationship to the root. In a C major chord, the note E is called the 3rd. It's called that because the interval between C and E is a 3rd.

Finally, intervals themselves are referred to as 2nds, 3rds, 4ths, and so on. These names are used even when we aren't referring to any particular scale or chord, but simply to the interval between two notes.

Thus we can use the term "3rd" to refer to an interval, a scale step, or a note within a chord. The name of the scale step or chord note is the same as the name of the interval between that step or chord note and the tonic note of the scale or the root of the chord - but when we say, "The 3rd of an F chord is A," we're referring to the note A itself as a 3rd. We're not talking, at that moment, about the interval between F and A, which is also a 3rd. This is important, because when we start talking about chords, we'll often refer to the notes within a chord as 3rds, 5ths, and so on.

Even though there is only one 3rd scale step within a given scale (the note that is a 3rd above the tonic note of the scale), each scale contains a number of intervals of a 3rd. Within the C major scale, the interval from D to F is a 3rd (a minor 3rd, as it happens), from D to G is a 4th, and so on. All of the intervals in the C major scale that are smaller than an octave are shown in Figure 2-6. This figure also indicates which of these intervals are major, minor, augmented, and diminished. Being able to grasp the interval relationships within the scale is an important part of learning to use chords.

To reiterate, the terms "3rd," "5th," "7th," and so forth can refer to three distinct things: They're the names of intervals, and they're also the names of notes within a particular scale or chord. In the latter case, the name indicates the interval that lies between the note and the root of the chord or the tonic of the scale - the nearest root or tonic below the note, to be a little more specific. For example, in an A scale, the 5th is E, because the interval from A up to E is a 5th.

In some music theory texts, these two usages are formatted using different typography. You may see the names of pure intervals spelled out (as third, fourth, fifth, etc.), while the names of notes within a scale or chord are formatted as ordinal numerals (3rd, 4th, 5th, etc.). In this book, I've chosen to use numerals for both usages, on the theory that nobody but typographers and copyeditors pays much attention to the difference in formatting.

Figure 2-6. Most of the examples earlier in this chapter use C as the lower note of the interval. Intervals can start on any note, however. Shown here are all of the intervals smaller than an octave that use the notes of the C major scale: 2nds (a), 3rds (b), 4ths (c), 5ths (d), 6ths (e), and 7ths (f). The type of each interval is shown. These interval relationships are the same in any major scale: For instance, if you start on the 2nd step of the scale and construct an interval of a 3rd, it will always be a minor 3rd.

MORE WAYS TO ALTER INTERVALS

If you're the type of person who likes to break the rules once in a while, you may look at Figure 2-5 and find yourself wondering, "What would happen if I made an interval by putting an E6 next to an F#? What sort of interval would that be? Or what if I combine a G# with a B6?"

These are real intervals. Useful ones, too. They even have names. When a major/minor-type interval (one based on a modal scale step) is stretched by an extra half-step, so that it's even bigger than a major, it's referred to as an augmented interval - the same term we've already met when talking about perfect (tonal) intervals that are enlarged by a half-step. Likewise, when a modal interval is narrowed by an extra half-step, it's called diminished.

Thus there are not two types of 2nds, 3rds, 6ths, and 7ths, but four - diminished, minor, major, and augmented. And 4ths and 5ths can be either widened or narrowed, so there are actually three types of 4ths and 5ths - diminished, perfect, and augmented. The full panoply of possibilities is shown in Figure 2-7

Figure 2-7. A more complete catalog of intervals, with a couple of examples of most types. Doubly augmented and doubly diminished intervals have been omitted from the examples, since they're rarely seen.

In case you were wondering, there's no such thing as a diminished unison. Once in a great while, though, you'll run into a doubly augmented or doubly diminished interval. For instance, the interval from C# up to B6 is a diminished 7th, so the interval C#-B66 would be a doubly diminished 7th. Double flats (66) and double sharps (##) are sometimes needed when notating music in keys that have lots of flats or sharps in their key signature. The rules for when and how to use them are discussed in the section "Chromatic Spelling" in Chapter Seven.

Calling the interval C#-E6 a diminished 3rd may seem needlessly academic and fussy. The interval consists of two half-steps - why not just call it a major 2nd? Well, you can call it that if you like. In the real world, it may not make a lot of practical difference. You'll still be able to communicate your ideas to other musicians. But later in this book, we'll see many chords that contain augmented and diminished intervals. An F7#5 chord, for instance, contains both C# and E6. Calling the interval a major 2nd would obscure the structure of the chord, for reasons that will be explained in Chapter Five. By learning the correct interval names, you'll build a solid foundation for more advanced concepts.