A Player's Guide to Chords and Harmony (5 page)

Figure 1-4. The 12 pitch classes. Each of the black keys on the keyboard has two possible names, while the white keys have only one name. This arrangement of note names (C, C#/D6, etc.) is repeated up and down the keyboard.

To look at it a slightly different way, we can say that the frequency spectrum is divided up into 12 groups of pitches called pitch classes, each of which contains seven or eight elements. All of the notes with the name C, for example, belong to the same pitch class. Figure 1-6 illustrates the idea of pitch classes.

Before going any further, we should note that in one sense, the set of frequencies we use, which is called the equal-tempered 12-note chromatic scale, is entirely arbitrary. We could as easily divide the frequency spectrum up in some other way. The number of potential scales (also called tuning systems) is infinite. But there are powerful pragmatic reasons why the chromatic scale musicians use every day is laid out as it is. I've included a fuller explanation of this in Appendix B, "The Harmonic Series and Equal Temperament:'

As noted above, pitched sounds vibrate at specific, discrete frequencies. Our ears are remarkably good at figuring out - at least in an intuitive sense - how rapidly the vibrations are occurring. We can't actually count the separate vibrations in a tone that's vibrating at a frequency of more than 10 or 12 cycles per sec ond, but some people can learn to identify tones that have specific frequencies, such as 440 cycles per second (a talent called "perfect pitch"), and most people can learn to identify relationships among frequencies (a talent called "relative pitch"). Those who are unable to do so even in a rudimentary way are referred to as tone-deaf.

Figure 1-5. One way to look at the chromatic scale is as a repeating series of 12-note groups, each of which contains the notes from A up to G#. Only a portion of the full chromatic scale is shown here; it extends both upward and downward.

Figure 1-6. In place of the grouping in Figure 1-4, we can look at the chromatic scale as consisting of 12 groups, each of which contains all of the notes that have the same letter-name. Here we see the grouped A's, A#'s, and B's. As in Figure 1-4, only a portion of each group is shown; the dotted lines indicate that the groups extend both upward and downward.

The easiest relationship to identify is when the frequency of one tone is the same as the frequency of another tone. As explained above in the section on "Playing In Tune," this relationship is called a unison. "Unison" is in fact a Latinderived word that means "one sound"

After the unison, the next easiest relationship for our ears to identify is when the frequency of one tone is twice or half the frequency of another. This relationship is called the octave. "Octave" comes from a Latin word that means "eight," a fact that will make more sense when we've covered a little more ground.

Tones that are an octave apart are felt to be so similar that they have the same name. If you're sitting in front of a piano, try playing all of the C keys, one at a time, from the bottom of the keyboard to the top. Assuming your piano is in tune, you should be able to sense the strong similarity among these tones. The lowest C on the piano has a frequency of about 32.7032Hz, and the frequency of each C as you progress up the keyboard is exactly twice this number, as shown in Figure 1-7.

If it seems odd to you that a nice, familiar note like C doesn't have a nice, round number for a frequency, you're right: It is odd. Many aspects of music, including the pitch of C, are based on traditions that have evolved over the centuries, not on common sense. The essential point is that the frequency doubles as we move up an octave - or, to look at it the other way, the frequency is cut in half each time we drop an octave.

Figure 1-7. Each note in the chromatic scale has twice the frequency of the note with the same name that's an octave below it. To look at it another way, doubling the frequency of a tone raises it by one octave. Shown here are the actual frequencies in Hz (cycles per second) of the note C in seven octaves.

This is true for each of the notes on the keyboard. The A above Middle C has a frequency of 440Hz. The A below Middle C has a frequency of 220Hz, the A below that is at 110Hz, and so on. There's not much point in going any lower than the bottom A (27.5Hz) on the piano keyboard, because this is close to the lower threshold of humans' ability to hear pitch.

If you count the keys on the keyboard between any note and the note an octave higher or lower, you'll find that (not including the octave repetition of the starting note) there are exactly 12 notes within any given octave. This is true no matter what note you choose as your starting point, as Figure 1-5 makes clear. Each octave of the chromatic scale is exactly like every other octave.

As Figure 1-4 shows, the white keys on the piano have letter-names: A, B, C, D, E, F, and G. There are seven of these notes, and they repeat in every octave. Starting with E, for instance, and proceeding up the keyboard using only the white keys, the seventh note is D. The next note, another E an octave above the first, is the eighth note. That's why octaves are called octaves - the term refers to the layout of white keys, not to the chromatic scale as a whole. If the term were derived from the 12-tone chromatic scale, we'd have to describe the interval in which the frequency is doubled or halved using the word "duodecimatives" or something equally horrible.

The layout of notes on the staff perfectly reflects the white-key layout of the keyboard: Each white key has its own line or space (see Figure 1-8). The black keys don't.

The keyboard and notation system we use today originated in the Middle Ages. Originally, the white keys were the only keys that existed. That's the main reason why the naming convention uses only seven letters. As time went on, com posers found it useful to add a few notes that were "in the cracks" between the white keys. Shorter keys, positioned above the main row of keys, were added. Some early keyboards didn't have five of these shorter keys in every octave; they only had two or three. Later, in the Renaissance, keyboards were sometimes built with more than five of the shorter keys. The F#/G6 key, for instance, might be a "split" key, which allowed the performer to play either of two slightly different pitches between F and G. The layout we have today is an effective compromise: There are enough keys to allow us to play a wide variety of chords and melodies, but not so many that playing the keyboard turns into a knuckle-banging nightmare.

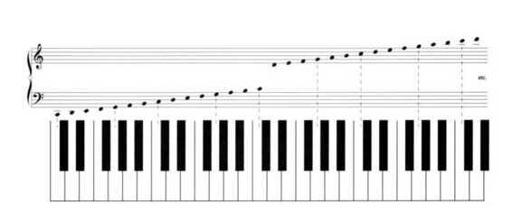
Figure 1-8. The layout of lines and spaces on the staff reflects the layout of the piano keyboard. Each white key gets its own line or space.

The fact that the relationships among white keys are considered basic, while the black keys were added on afterward, accounts for some other important bits of terminology. The distance between two adjacent white keys that have a black key between them is called a whole-step (see Figure 1-9). The relationship between any white key and the black key that lies next to it is called a half-step. In fact, there's nothing particularly "whole" about a whole-step. If you play guitar, it will be obvious that this entire naming convention - letter-names, whole-steps, and half-steps - is more than a bit arbitrary, because on a guitar the basic unit of the scale is the half-step (a distance of one fret up or down). The only way to play a note that's half a fret away from another note is by bending the string, an action that takes you entirely outside the scale we're talking about.

Another term for half-step is semitone. "Semi-" is a Latin prefix that means "half" The corresponding term for a whole-step would be "tone," but except in a few textbooks the word is no longer used in this way - except in one particular instance. The interval of an augmented fourth or diminished fifth, which we'll meet in Chapter Two, is called a tritone, a term that means "three tones.' A tritone consists of three intervals, each a tone in width, stacked one on top of the other.

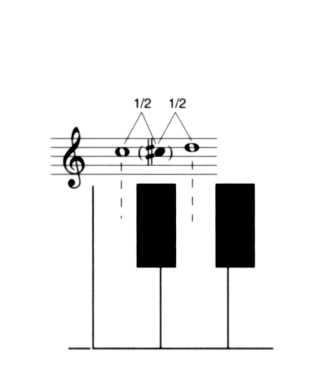
Figure 1-9. A whole-step (in this case, from C to D), contains two half-steps (in this case, C to C# and C# to D).

The other term that derives from the keyboard layout is accidental. The black keys were not originally felt to be an entirely legitimate part of the scale, the way the white keys were. They were sort of harmonic accidents. This term has a more direct meaning in terms of key signatures, which we'll get to below. But if you think of the black keys as being accidental in terms of the scale you hear when you play the white keys, you'll be right on the money.

DO-RE-MI

If you play the white keys on the keyboard, starting at C and playing each key until you arrive back at C, you'll produce a familiar-sounding scale. This is called the major scale, because the first and third notes (C and E) form the interval of a major 3rd. We'll take a more systematic look at this interval, and how it relates to other intervals, in Chapter Two.

If you look at the arrangement of white and black keys on the keyboard (see Figure 1-10), you'll see that the major scale is made up of a pattern of whole-steps and half-steps. This pattern (two whole-steps followed by a half-step, and then three more whole-steps followed by another half-step) is what defines the major scale. Other scales can be built by combining whole-steps and half-steps in different ways. We'll look at some of the more useful alternatives in Chapter Seven.