Why Beauty is Truth (6 page)

The most popular tourist site in Siwa is Aghurmi, a former temple dedicated to the god Amun. So holy was Amun that his main aspect was entirely abstract, but he became associated with a more physical entity, the provenance of the god Re, the Sun. Constructed during the 26th Dynasty, the temple of Amun at Siwa was the home of a famous oracle that is particularly associated with two major historical events.

The first is the destruction of the army of Cambyses II, a Persian king who conquered Egypt. It is said that in 523 BCE, planning to use the oracle of Amun to legitimate his rule, Cambyses sent a military force into the Western Desert. The army reached Bahariya Oasis but was destroyed in a sandstorm on its way to Siwa. Many Egyptologists suspect that the “lost army of Cambyses” may be mythical, but in 2000 a team from Helwan University, looking for oil, found bits of cloth, metal, and human remains in the area, and suggested that these might be the remains of the lost army.

The second event, two centuries later, is historical fact: a fateful visit to Siwa by Alexander the Great, who was after exactly the same thing as Cambyses.

Alexander was the son of King Philip II of Macedon. Philip's daughter Cleopatra of Macedon married King Alexander of Epirus, and Philip was assassinated during the proceedings. The killer may have been Philip's homosexual lover Pausanias, who was upset because the king had not done anything about some complaint or other that Pausanias had made. Or the murder may have been a Persian plot set up by Darius III. If so, it backfired, because the Macedonian army immediately proclaimed Alexander king, and the 20-year-old monarch famously went on to conquer most of the known world. Along the way, in 332 BCE, he conquered Egypt without a fight.

Intent on cementing this conquest with an endorsement of his credentials as pharaoh, Alexander made a pilgrimage to Siwa to ask the oracle whether he was a god. He visited the oracle alone, and on his return announced its verdict: yes, the oracle had confirmed that he truly was a god. This verdict became the primary source of his authority. Later, rumors claimed that the oracle had revealed him to be the son of Zeus.

It is not clear whether the Egyptians were convinced by this rather flimsy evidence or whether, given Alexander's control of a substantial army, they found it prudent to go along with his story. Perhaps they were fed up with the rule of the Persians and considered Alexander the lesser of two evils—he had been welcomed with open arms by the former Egyptian capital of Memphis for precisely that reason. Whatever the truth behind the history, from that time on, the Egyptians venerated Alexander as their king.

On the way to Siwa, fascinated by an area of the country lying between the Mediterranean Sea and the lake that came to be known as Mareotis, Alexander decided to have a city constructed there. The city, which he modestly named Alexandria, was designed by Donocrates, a Greek architect, after a basic plan sketched by Alexander himself. The city's birth has been dated by some to 7 April 331 BCE; this date is disputed by others, but it must be close to 334 BCE. Alexander never saw his creation; his next visit to the area was to be buried there.

So, at least, goes the time-honored legend, but the truth is probably more complex. It now appears that much of what later became Alexandria already existed when Alexander arrived. Egyptologists discovered long ago that many inscriptions are not all that trustworthy. The great Temple at Karnak, for instance, is riddled with cartouches of Ramses II. But much of it was actually constructed by his father, Seti I, and traces—
not always faint—of the father's inscriptions can be seen beneath those carved for Ramses. Such usurpation was commonplace, and was not even considered disrespectful. In contrast, “defacing” a predecessor's reliefs—hacking out the pharaoh's face—was most definitely disrespectful, intentionally depriving that predecessor of his place in the afterlife by destroying his very identity.

Alexander had his name carved all over the buildings of ancient Alexandria. He had his name carved, so to speak, on the city itself. Where other pharaohs usurped the odd building or monument, Alexander usurped an entire city.

Alexandria became a major seaport, connected by branches of the Nile and a canal to the Red Sea and thence to the Indian Ocean and the Far East. It became a center of learning, with a celebrated library. And it was the birthplace of one of the most influential mathematicians in history: the geometer Euclid.

We know much more about Alexander than we do about Euclid—even though Euclid's long-term influence on human civilization was arguably greater. If there can be such a thing as a household name in mathematics, “Euclid” is it. Although we know little about Euclid's life, we know a lot about his works. For several centuries, mathematics and Euclid were pretty much synonymous throughout the Western world.

Why did Euclid become so well known? There have been greater mathematicians, and more significant ones. But for close to two thousand years Euclid's name was known to every student of mathematics across the whole of Western Europe, and to a lesser extent in the Arab world as well. He was the author of one of the most famous mathematics texts ever written: the
Elements of Geometry
(usually shortened to
Elements
). When printing was invented, this work was among the first books to appear in printed form. It has been published in over a thousand different editions, a number exceeded only by the Bible.

We know slightly more about Euclid than we do about Homer. He was born in Alexandria around 325 BCE and died in about 265 BCE.

Having said that, I am uncomfortably aware that I already need to backtrack. That Euclid existed and was sole author of the
Elements
is only one of three theories. The second is that he existed but did not write the
Elements
, at least not on his own. He may have been the leader of a team of
mathematicians who collectively produced the
Elements.
The third theory—far more contentious but within the bounds of possibility—is that the team existed, but much like the group of mostly French, mostly young mathematicians who wrote under the name “Nicolas Bourbaki” in the mid-twentieth century, they took “Euclid” as a collective pseudonym. Nevertheless, the most likely story seems to be that Euclid existed, that he was one person, and that he composed the
Elements
himself.

This does not mean that Euclid discovered all of the mathematics contained within his book's pages. What he did was to collect and codify a substantial part of ancient Greek mathematical knowledge. He borrowed from his predecessors and he left a rich legacy for his successors, but he also stamped his own authority on the subject. The
Elements
is generally described as a geometry book, but it also deals with number theory and a kind of prototypical algebra—all of it presented in geometrical guise.

Of Euclid's life we know very little. Later commentators included a few snippets of information in their works, none of which modern scholars can substantiate. They tell us that Euclid taught in Alexandria, and it is usual to infer that he was born in that city, but we don't actually know that. In 450 AD, in an extensive commentary on Euclid's mathematics written more than seven centuries after his death, the philosopher Proclus wrote:

Euclid . . . put together the
Elements
, arranging in order many of Eudoxus's theorems, perfecting many of Theaetetus's, and also bringing to irrefutable demonstration the things which had been only loosely proved by his predecessors. This man lived in the time of the first Ptolemy; for Archimedes, who followed closely upon the first Ptolemy, makes mention of Euclid, and further they say that Ptolemy once asked him if there were a shorter way to study geometry than the
Elements
, to which he replied that there was no royal road to geometry. He is therefore younger than Plato's circle, but older than Eratosthenes and Archimedes; for these were contemporaries, as Eratosthenes somewhere says. In his aim he was a Platonist, being in sympathy with this philosophy, whence he made the end of the whole
Elements
the construction of the so-called Platonic figures.

The treatment of some topics in the
Elements
provides indirect but compelling evidence that Euclid must at some point have been a student at Plato's Academy in Athens. Only there, for example, could he have
learned about the geometry of Eudoxus and Theaetetus. As for his character, all we have are some fragments from Pappus, who described him as “most fair and well disposed towards all who were able in any measure to advance mathematics, careful in no way to give offence, and although an exact scholar, not vaunting himself.” A few anecdotes survive, such as one told by Stobaeus. One of Euclid's students asked him what he would get through an understanding of geometry. Euclid called his slave and said, “Give him a coin, since he must make a profit from what he learns.”

The Greek attitude to mathematics was very different from that of the Babylonians or the Egyptians. Those cultures saw mathematics largely in practical terms—although “practical” could mean aligning shafts through a pyramid so that the
ka
of the dead pharaoh could be launched in the direction of Sirius. For some Greek mathematicians, numbers were not tools occasionally employed in support of mystical beliefs, but the very core of those beliefs.

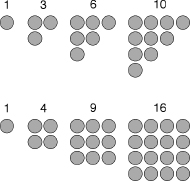
Aristotle and Plato tell of a cult, centered on Pythagoras, that flourished around 550 BCE and that viewed mathematics, especially number, as the basis of the whole of creation. They developed mystical ideas about the harmony of the universe, based in part on the discovery that harmonious notes on a stringed instrument are related to simple mathematical patterns. If a string produces a certain note, a string of half the length produces a note one octave higher—the most harmonious of all intervals. They investigated various number patterns, in particular polygonal numbers, formed by arranging objects in polygonal patterns. For instance, the “triangular numbers” 1, 3, 6, and 10 are formed from triangles, and the “square numbers” 1, 4, 9, and 16 are formed from squares: