Why Beauty is Truth (4 page)

Nabu-Shamash was born into a typical “upper-class” household in the Old City of Babylon, not far from the Libil-hegalla canal and close to the justly famed Ishtar Gate, a ceremonial entrance decorated with colored ceramic bricks in fanciful forms—bulls, lions, even dragons. The road through the Ishtar Gate was impressive, reaching a width of 20 meters; it was paved with limestone flags on top of a bed of asphalt, with a brick foundation. Its name was “May the enemy not have victory”—rather typical of Babylon's main street names—but it is generally known as the Processional Way, being used by the priests to parade the god Marduk through the city when ceremony so decreed.

The family home was built of mud brick, with walls six feet thick to keep out the sun. The external walls had few openings—mainly a doorway at street level—and rose to a height of three stories, with lighter materials, mainly wood, being used for the top floor. The family owned many slaves, who performed routine household tasks. Their quarters, along with the kitchen, were to the right of the entrance. The family rooms were to the left: a long living room, bedrooms, and a bathroom. There was no bathtub in Nabu-Shamash's time, though some have survived from other eras. Instead, a slave would pour water over the bather's head and body, approximating a modern shower. A central courtyard opened to the sky, and toward the back were storerooms.

Nabu-Shamash's father was an official in the court of a king, name unknown, whose reign preceded Nebuchadnezzar I. His duties were largely bureaucratic: he was responsible for administering an entire district, ensuring that law and order were maintained, that the fields were properly irrigated, and that all necessary taxes were collected and paid. Nabu-Shamash's father had also been trained as a scribe, because literacy and numeracy were basic skills for anyone in the Babylonian equivalent of the civil service.

According to a decree attributed to the god Enlil, every man should follow in his father's footsteps, and Nabu-Shamash was expected to do just that. However, scribal abilities also opened up other career paths, notably that of priest, so his training paved the way to a choice of professions.

We know what Nabu-Shamash's education was like because extensive records, written in Sumerian by people who were trained as scribes, have survived from roughly the period concerned. These records make it plain that Nabu-Shamash was fortunate in his choice of parentage, for only the sons of the well-to-do could hope to enter the scribal schools. In fact, the quality of Babylonian education was so high that foreign nobles sent their sons to the city to be educated.

The school was called the Tablet House, presumably referring to the clay tablets used for writing and arithmetic. It had a head teacher, referred to as the “Expert” and as the “Father of the Tablet House.” There was a class teacher, whose main task was to make the boys behave themselves; there were specialist teachers in Sumerian and mathematics. There were prefects, called “Big Brothers,” whose job included keeping order. Like all students, Nabu-Shamash lived at home and went to school during the day,
for around 24 days each 30-day month. He had three days off for recreation, and a further three for religious festivals.

Nabu-Shamash began his studies by mastering the Sumerian language, especially its written form. There were dictionaries and grammatical texts to be studied, and long lists to be copied—legal phrases, technical terms, names. Later, he progressed to mathematics, and it was then that his studies became central to our tale.

What did Nabu-Shamash learn? For everyone but philosophers, logicians, and professional mathematicians who are being pedantic, a number is a string of digits. Thus the year in which I write this sentence is 2006, a string of four digits. But as the pedants will jump to remind us, this string of digits is not the number at all but only its notation, and a rather sophisticated form of notation at that. Our familiar decimal system employs just ten digits, the symbols 0 through 9, to represent any number, however large. An extension of that system also permits the representation of very small numbers; more to the point, it permits the representation of numerical measurements to very high levels of precision. Thus the speed of light, according to the best current observations, is approximately 186,282.397 miles per second.

We are so familiar with this notation that we forget how clever it is—and how difficult to grasp when we first encounter it. The key feature on which all else rests is this: the numerical value of a symbol, such as 2, depends on where it is placed relative to the other symbols.
The symbol 2 does not have a fixed meaning independent of its context.
In the number representing the speed of light, the digit “2” immediately before the decimal point does indeed mean “two.” But the other occurrence of “2” in that number means “two hundred.” In the date 2006, that same digit means “two thousand.”

We would be exceedingly unhappy to have a system of writing in which the meaning of a letter depended on where it occurred in a word. Imagine, for instance, what reading would be like if the two a's in “alphabet” had totally different meanings. But positional notation for numbers is so convenient and powerful that we find it hard to imagine that anyone really used any other method.

It was not always thus. Our present notation dates back no more than 1500 years, and was first introduced into Europe a little more than 800
years ago. Even today, different cultures use different symbols for the same decimal digits—look at any Egyptian banknote. But ancient cultures wrote numbers in all sorts of strange ways. The most familiar to us is probably the Roman system, in which 2006 becomes MMVI. In ancient Greek it would be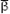
ζ. In place of our 2, 20, 200, and 2000, the Romans wrote II, XX, CC, and MM, and the Greeks wrote β, κ, α, and
.

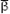Babylonian base–60 numerals.

The Babylonians were the earliest known culture to use something akin to our positional notation. But there was one significant difference. In the decimal system, every time a digit is moved one place to the left, its numerical value is multiplied by ten. So 20 is ten times 2, and 200 is ten times 20. In the Babylonian system, each move to the left multiplies a number by sixty. So “20” would mean 2 times 60 (120 in our notation) and “200” would mean 2 times 60 times 60 (7200 in our notation). Of course, they didn't use the same “2” symbol; they wrote the number “two” using two copies of a tall, thin wedge symbol, as shown in the figure above. Numbers from one to nine were written by grouping that many copies of the tall wedge. For numbers greater than nine, they added another symbol, a sideways wedge, which denoted the number ten, and they used groups of these symbols to denote twenty, thirty, forty, and fifty. So, for instance, our “42” was four sideways wedges followed by two tall wedges.

For reasons we can only guess at, this system stopped at 59. The Babylonians did not group six sideways wedges to make 60. Instead, they reverted to the tall thin wedge previously used to mean “one,” and used it to mean “one times sixty.” Two such wedges meant 120. But they might also mean “two.” Which meaning was intended had to be inferred from context, and from the position of the symbols relative to each other. For example, if there were two tall wedges, a space, and two more tall wedges, then the first group meant “one hundred twenty” and the second “two”—much as the two symbols 2 in our 22 mean twenty and two respectively.

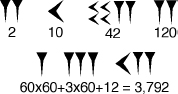
This method extended to much larger numbers. A tall wedge could mean 1, or 60, or 60 × 60 = 3,600, or 60 × 60 × 60 = 216,000, and so on. The three bottom groups in the figure indicate 60 × 60 + 3 × 60 + 12, which we would write as 3,792. A big problem here is that the notation has some ambiguities. If all you see is two tall wedges, does this mean 2, 60 × 2, or 60 × 60 × 2? Does a sideways wedge followed by two tall ones mean 12 × 60 + 2 or 12 × 60 × 60 + 2, or even 10 × 60 × 60 + 2 × 60? By Alexander the Great's time, the Babylonians had removed these ambiguities by using a pair of diagonal wedges to indicate that no number occurred in a given slot; in effect, they had invented a symbol for zero.

Why did the Babylonians use this sexagesimal system rather than the familiar decimal system? They may have been influenced by a useful feature of the number 60: its large variety of divisors. It is divisible exactly by the numbers 2, 3, 4, 5, and 6. It is also divisible by 10, 12, 15, 20, and 30. This feature is rather pleasant when it comes to sharing things, such as grain or land, among several people.

A final feature may well have been decisive: the Babylonian method of measuring time. It seems that they found it convenient to divide a year into 360 days, although they were excellent astronomers and knew that 365 was closer, and 365¼ closer still. The lure of the arithmetical relationship 360 = 6 × 60 was too strong. Indeed, when referring to time, the Babylonians suspended the rule that moving symbols one slot to the left multiplied their value by sixty, and replaced that by six, so that what should have meant 3,600 was actually interpreted as 360.