Why Beauty is Truth (10 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart


Algebra really arrived on the mathematical scene in 830, when the main action moved from the Greek world to the Arabic one. In that year the astronomer Mohamed ibn Musa al-KhwÄrizmÄ« wrote a book called
al-Jabr w'al Muqâbala
, which translates roughly as “restoration and simplification.”
The words refer to standard techniques for manipulating equations so as to put them into a better form for solution. From
al-jabr
comes our word “algebra.” The first Latin translation in the twelfth century bears the title
Ludus Algebrae et Almucgrabalaeque.
Al-KhwÄrizmÄ«'s book contains hints of earlier influences, Babylonian and Greek, and also rests on ideas introduced in India by Brahmagupta around 600. It explains how to solve linear and quadratic equations. Al-KhwÄrizmÄ«'s immediate successors worked out how to solve a few special kinds of cubic. Among them are Tâbit ibn Qorra, a doctor, astronomer, and philosopher who lived in Baghdad and was a pagan, and an Egyptian named al-Hasan ibn al-Haitham, generally referred to in later Western writings as Alhazen. But the most famous of them all is Omar Khayyám.
Omar bore the full name Ghiyath al-Din Abu'l-Fath Umar ibn Ibrahim Al-Nisaburi al-Khayyámi. The word “al-Khayyámi” translates literally as “tent-maker,” which some scholars believe may have been the trade of his father Ibrahim. Omar was born in Persia in 1047, and spent most of his productive life at Naishapur. You can find it in an atlas as Neyshabur, a city near Masshad in the Khorosan province of northeastern Iran, close to the border with Turkmenistan.
Legend has it that in his youth, Omar left home to study Islam and the Quran under the celebrated cleric Imam Mowaffak, who lived in Naishapur. There he struck up a friendship with two fellow students, Hasan Sabah and Nizam al-Mulk, and the three of them made a pact. If any of them became rich and famousânot unlikely for students of Mowaffakâthat person would share his wealth and power with the other two.
The students completed their studies and the years flew by; the pact remained in force. Nizam traveled to Kabul. Omar, politically less ambitious, spent some time as a tent-makerâanother possible explanation of the name “Al-Khayyámi.” Science and mathematics became his passions, and he spent most of his spare time on them. Eventually Nizam returned, secured a position in the government, and became administrator of affairs to the sultan Alp Arslan, with an office in Naishapur.
Since Nizam was now rich and famous, Omar and Hasan claimed their rights under the pact. Nizam asked the sultan for permission to assist his friends, and when it was granted he honored the agreement. Hasan received a well-paid government job, but Omar merely wished to continue his scientific studies in Naishapur, where he would pray for the health and
well-being of Nizam. His old school friend arranged for Omar to be given a government salary, to free his time for study, and the deal was done.
Hasan later tried to overthrow a senior official and lost his sinecure, but Omar continued serenely on and was appointed to a commission whose mandate was to reform the calendar. The Persian calendar was based on the movements of the sun, and the date of the first day of the new year was subject to change, which was confusing. It was just the job for a competent mathematician, and Omar applied his knowledge of mathematics and astronomy to calculate when New Year's Day should fall in any given year.
Around this time, he also penned the
Rubaiyat
, which loosely translates as “quatrains,” a poetic form. A
rubai
was a four-line verse with a rather specific rhyming patternâmore accurately, one of two possible patternsâand a
rubaiyat
was a collection of verses in this form. One verse makes a clear reference to his work on reforming the calendar:
Ah, but my computations, People say,
Reduced the Year to better Reckoning? Nay,
'Twas only striking from the Calendar
Unborn To-morrow and dead Yesterday.
Omar's verses were distinctly nonreligious. Many of them praise wine and its effects. For instance:
And lately, by the Tavern Door agape,
Came shining through the Dusk an Angel Shape
Bearing a Vessel on his Shoulder; and
He bid me taste of it; and 'twasâthe Grape!
There are wry allegorical references to wine, as well:
Whether at Naishápúr or Babylon,
Whether the Cup with sweet or bitter run,
The Wine of Life keeps oozing drop by drop,
The Leaves of Life keep falling one by one.
Other verses poke fun at religious beliefs. One wonders what the Sultan thought of the man he had put on retainer, and what the imam thought of the outcome of his teaching.
Meanwhile, the disgraced Hasan, having been forced to leave Naishapur, fell in with a gang of bandits and made use of his superior education to become its leader. In the year 1090 those bandits, under Hasan's command, captured Alamut castle in the Elburz Mountains, just south of the Caspian Sea. They terrorized the region, and Hasan became notorious as the Old Man of the Mountains. His followers, known as the
Hashishiyun
for their use of the drug hashish (a very potent form of cannabis), built six mountain fortifications, from which they would emerge to kill carefully selected religious and political figures. Their name was the origin of the word “assassin.” So Hasan managed to become rich and famous in his own right, as befitted a student of Mowaffak, though he was not, by this time, disposed to share his fortune with his old schoolmates.
While Omar calculated astronomical tables and worked out how to solve the cubic, Nizam pursued his political career until, in a touch of exquisite irony, Hasan's bandits assassinated him. Omar lived on to the age of 76, dyingâso it is saidâin 1123. Hasan died the following year, aged 84. The assassins continued to wreak political havoc until they were wiped out by the Mongols, who conquered Alamut in 1256.

To return to Omar's mathematics: Around 350 BCE the Greek mathematician Menaechmus discovered the special curves known as “conic sections,” which he used, scholars believe, to solve the problem of doubling the cube. Archimedes developed the theory of these curves, and Apollonius of Perga systematized and extended the subject in his book
Conic Sections.
What particularly interested Omar Khayyám was the Greek discovery that conic sections could be used to solve certain cubic equations.
Conic sections are so named because they can be obtained by slicing a cone with a plane. More properly, a
double
cone, like two ice-cream cones joined at their sharp ends. A single cone is formed by a collection of straight-line segments, all meeting at one point and passing through a suitable circle, the “base” of the cone. But in Greek geometry you can always extend straight-line segments as far as you wish, and the result is to create a double cone.
The three main types of conic section are the ellipse, parabola, and hyperbola. An ellipse is a closed oval curve that arises when the cutting plane passes through only one half of the double cone. (A circle is a special kind of ellipse, created when the plane is exactly perpendicular to the cone's
axis.) A hyperbola consists of two symmetrically related open curves, which in principle extend to infinity, that arise when the cutting plane passes through both halves of the double cone. The parabola is a transitional form, a single open curve, and in this case the cutting plane must be parallel to one of the lines lying on the surface of the cone.
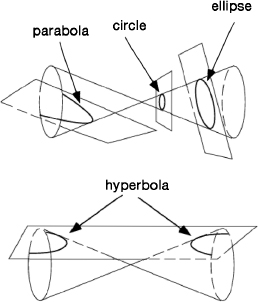
Conic sections.
At great distances from the tip of the cone, the curves of a hyperbola become ever closer to two straight lines, which are parallel to the lines where a parallel plane through the tip would cut the cone. These lines are called
asymptotes.
The Greek geometers' extensive studies of conic sections constituted their most significant area of progress beyond the ideas codified by Euclid. These curves remain vitally important in today's mathematics, but for quite different reasons from those that interested the Greeks. From the algebraic point of view, they are the next simplest curves after the straight line. They are also important in applied science. The orbits of planets in the solar system are ellipses, as Kepler deduced from Tycho Brahe's observations of Mars. This elliptical orbit is one of the observations that led Newton to formulate his famous “inverse square law” of gravity. This in turn led to the realization that some aspects of the universe exhibit clear
mathematical patterns. It opened up the whole of astronomy by making planetary phenomena computable.

The majority of Omar's extant mathematics is devoted to the theory of equations. He considered two kinds of solution. The first, following the lead of Diophantus, he called an “algebraic” solution in whole numbers; a better adjective would be “arithmetic.” The second kind of solution he called “geometric,” by which he meant that the solution could be constructed in terms of specific lengths, areas, or volumes by geometrical means.
Making liberal use of conic sections, Omar developed geometric solutions for all cubic equations, and explained them in his
Algebra
, which he completed in 1079. Because negative numbers were not recognized in those days, equations were always arranged so that all terms were positive. This convention led to a huge number of case distinctions, which nowadays we would consider to be essentially the same except for the signs of the numbers. Omar distinguished
fourteen
different types of cubic, depending on which terms appear on each side of the equation. Omar's classification of cubic equations went like this:
cube = square + side + number
cube = square + number
cube = side + number
cube = number
cube + square = side + number
cube + square = number
cube + side = square + number
cube + side = number
cube + number = square + side
cube + number = square
cube + number = side
cube + square + side = number
cube + square + number = side
cube + side + number = square
