What If? (43 page)
Authors: Randall Munroe

SAT Guessing
Q.
What if everyone who took the SAT guessed on every multiple-choice question? How many perfect scores would there be?
—Rob Balder
A.
None.
Th
e SAT is a standardized test given to American high school students.
Th
e scoring is such that under certain circumstances, guessing an answer can be a good strategy. But what if you
guessed
on everything?
Not all of
the
SAT
is multiple-choice, so let’s focus on the multiple-choice questions to keep things simple. We’ll assume everyone gets the essay questions and fill-in-the-number sections correct.
In the 2014 version of the SAT, there were 44 multiple-choice questions in the math (quantitative) section, 67 in the critical reading (qualitative) section, and 47 in the newfangled
1
writing section. Each
question has five options, so a random guess has a 20 percent chance of being right.

Th
e probability of getting all 158 questions right is:
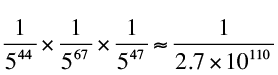
Th
at’s one in 27 quinquatrigintillion.
If all four million 17-year-olds took the SAT, and they all guessed randomly,
it’s a virtually certain that there would be no perfect scores on any of the three sections.
How certain is it? Well, if they each used a computer to take the test a million times each day, and continued this every day for five billion years
—
until the Sun expanded to a red giant and the Earth was charred to a cinder
—
the chance of any of them ever getting a perfect score on just the math section
would be about 0.0001 percent.
How unlikely is that? Each year something like 500 Americans are struck by lightning (based on an average of 45 lightning deaths and a 9–10 percent fatality rate).
Th
is suggests that the odds of any one American being hit in a given year are about 1 in 700,000.
2
Th
is means that the odds of acing the SAT by guessing are worse than the odds of every living
ex-President and every member of the main cast of
Firefly
all being independently struck by lightning . . . on the same day.
To everyone taking the SAT this year, good luck
—
but it won’t be enough.
- 1
I took the
SAT
a long time ago, okay?
- 2
See: xkcd, “Conditional Risk,”
http://xkcd.com/795/
.
Neutron Bullet
Q.
If a bullet with the density of a neutron star were fired from a handgun (ignoring the how) at the Earth’s surface, would the Earth be destroyed?
—Charlotte Ainsworth
A.
A bullet with the
density of a neutron star would weigh about as much as the Empire State Building.
Whether we fired it from a gun or not, the bullet would fall straight through the ground,
punching through the crust as if the rock were wet tissue paper.
We’ll look at two different questions:
- What would the bullet’s passage do to the Earth?
- If we kept the bullet here on the surface, what would it do to its surroundings? Could we touch it?
First, a little bit of background:
What are neutron stars?
A neutron star is what’s left over after a giant star
collapses under its own gravity.
Stars exist in a balance.
Th
eir massive gravity is always trying to make them collapse inward, but that squeezing sets off several different forces that push them back apart.
In the Sun, the thing holding off collapse is heat from nuclear fusion. When a star runs out of fusion fuel, it contracts (in a complicated process involving several explosions) until
the collapse is stopped by the quantum laws that keep matter from overlapping with other matter.
1
If the star is heavy enough, it overcomes that quantum pressure and collapses further (with another, more massive explosion) to become a neutron star. If the remnant is even heavier, it becomes a black hole.
2
Neutron stars are some of the densest objects you can find (outside of the infinite
density of a black hole).
Th
ey’re crushed by their own immense gravity into a compact quantum-mechanical soup that’s in some ways similar to an atomic nucleus the size of a mountain.
Is our bullet made from a neutron star?
No. Charlotte asked for a bullet
as dense
as a neutron star, not one made from actual neutron star material.
Th
at’s good, because you can’t make a bullet from that
stuff. If you take neutron star material outside of the crushing gravity well where it’s normally found, it will re-expand into superhot normal matter with an outpouring of energy more powerful than any nuclear weapon.
Th
at’s presumably why Charlotte suggested we make our bullet out of some magical, stable material that’s
as dense
as a neutron star.
What would the bullet do to the Earth?
You could imagine firing it from a gun,
3
but it might be more interesting to simply drop it. In either case, the bullet would accelerate downward, punch into the ground, and burrow toward the center of the Earth.
Th
is wouldn’t destroy the Earth, but it would be pretty strange.
As the bullet got within a few feet of the ground, the force of its gravity would yank up a huge clump of dirt,
which would ripple wildly around the bullet as it fell, spraying in all directions. As it went in, you’d feel the ground shake, and it would leave a jumbled, fractured crater with no entry hole.
Th
e bullet would fall straight through the Earth’s crust. On the surface, the vibration would quickly die down. But far below, the bullet would be crushing and vaporizing the mantle in front of it
as it fell. It would blast the material out of the way with powerful shockwaves, leaving a trail of superhot plasma behind it.
Th
is would be something never before seen in the history of the universe: an underground shooting star.

Eventually, the bullet would come to rest, lodged in the nickel-iron core at the center of the Earth.
Th
e energy delivered to the Earth would be massive on a human scale, but the planet would barely notice.
Th
e bullet’s gravity would affect only the rock within a few dozen feet of it; while it’s heavy enough to fall through the crust, its gravity alone wouldn’t be strong enough
to crush the rock very much.
Th
e hole would close up, leaving the bullet forever out of anyone’s reach.
4
Eventually, the Earth would be consumed by the aging, swollen Sun, and the bullet would reach its final resting place at the Sun’s core.
Th
e Sun isn’t dense enough to become a neutron star itself. After it swallows the Earth, it will instead go through some phases of expansion and
collapse, and will eventually settle down, leaving behind a small white dwarf star with the bullet still lodged in the center. Someday, far in the future
—
when the universe is thousands of times older than it is today
—
that white dwarf will cool and fade to black.
Th
at answers the question of what would happen if the bullet were fired into the Earth. But what if we could keep it near the surface?
Set the bullet on a sturdy pedestal
First, we’d need a magical infinitely strong pedestal to put the bullet on, which would need to sit on a similarly strong platform large enough to spread the weight out. Otherwise, the whole thing would sink into the ground.
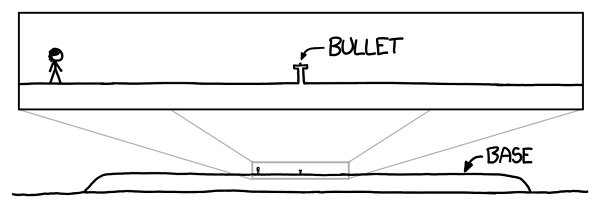
A base about the size of a city block would be strong enough to keep it above-ground for at least a few days, probably much more. After all, the Empire State Building
—
which weighs as much as our bullet
—
rests on a similar platform, and it’s more than a few days old
[citation needed]
and hasn’t disappeared into the ground.
[citation needed]
Th
e bullet wouldn’t vacuum up the atmosphere.
It would definitely compress the air around it and warm it up a little, but surprisingly, not really enough to notice.
Can I touch it?
Let’s imagine what would happen if you tried.
Th
e gravity from this thing is strong. But it’s not
that
strong.
Imagine you’re standing 10 meters away. At this distance, you feel a very slight tug in the direction of the pedestal. Your brain
—
not
accustomed to nonuniform gravities
—
thinks you’re standing on a gentle slope.

Do not put on roller skates.
Th
is perceived slope
gets steeper as you walk toward the pedestal, as if the ground were tipping forward.
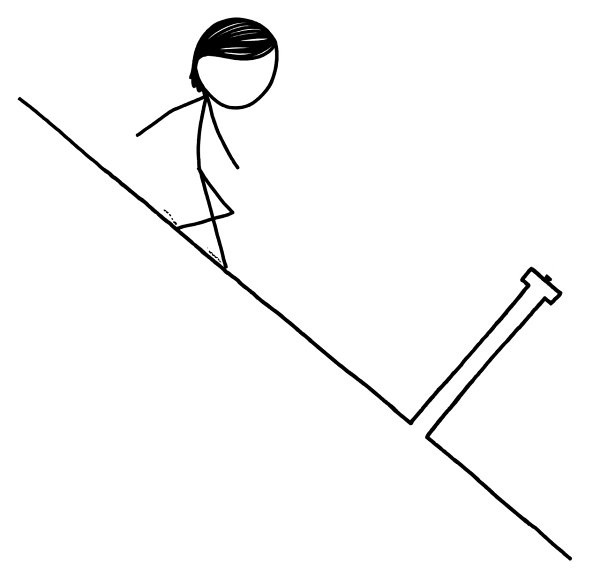
When you get within a few meters, you have a hard time not sliding forward. However, if you got a good grip on something
—
a handle or a signpost
—
you can get pretty close.
Los Alamos physicists might call this “tickling the dragon’s tail.”
But I wanna touch it!
To get close enough to touch it, you would need a
very
good grip on something. Really, you’d need to do this in a full-body support harness, or at the very least a neck brace; if you get within reach, your head will weigh as much as a small child, and your blood won’t know which way
to flow. However, if you’re a fighter pilot who’s used to gee forces, you might be able to pull it off.
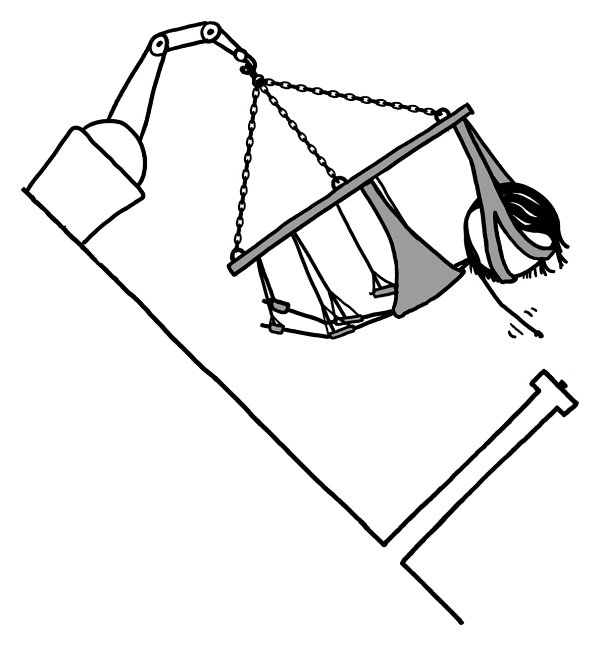
From this angle, the blood is rushing to your head, but you’d still be able to breathe.
As you stretch out your arm, the pull gets a
lot
stronger; 20 centimeters (about 8 inches) is the point of no return
—
as your fingertips cross that line, your arm becomes too heavy to pull back. (If you do a lot of one-handed pull-ups, you might be able to go a little closer.)
Once you
get within a few inches, the force on your fingers is overwhelming, and they’re yanked forward
—
with or without you
—
and your fingertips actually touch the bullet (probably dislocating your fingers and shoulder).
When your fingertip actually comes in contact with the bullet, the pressure in your fingertips becomes too strong, and your blood breaks through the skin.
In
Firefly,
River Tam
famously commented that “the human body can be drained of blood in 8.6 seconds given adequate vacuuming systems.”
