Warped Passages (73 page)

3
. A hypersphere is defined by
x
1
2
+
x
2
2
+…+
x
n
2
=
r
2
. Here
x
i
refers to the
i
th coordinate (the location in the
i
th dimension) and
r
is the radius of the hypersphere. The cross-section of the hypersphere when it crosses a fixed location in the
n
th dimension,
x
n
−
d
, is described by the equation
x
1
2
+
x
2
2
+…+
x
n
-1
2
=
r
2
−
d
2
. This is the equation of a hypersphere of one lower dimension and radius √(
r
2
−
d
2
). So, for example, when
n
= 3 and a sphere crosses Flatland, Flatlanders would see circles. (They would see disks if they saw the circles and their interiors, which would be mathematically described with an inequality.)
4
. Calabi-Yau manifolds are not the only possible stringy hidden manifolds. We now know that others, such as ones called G2 holonomy manifolds, might also give acceptable models.
5
. In string theory, we also sometimes use the word “brane” to mean space-filling branes that have the same number of dimensions as the higher-dimensional space. Here, however, we will concern ourselves only with branes that have fewer dimensions than the full higher-dimensional space, so I will restrict myself to the use of the term as described in the text.
6
. A brane that extends in the dimensions
x
1
,…,
x
j
is described by the
n
−
j
equations
x
j
+ 1 =
c
j
+ 1,
x
j
+ 2 =
c
j
+ 2 =…, =
x
n
=
c
n
, where
x
i
are coordinates,
n
is the number of dimensions of space, and
c
i
are fixed constants describing the location of the brane. More complicated branes that curve in the given coordinate system are described by more complicated equations that describe the surface.
7
. In equation form, Newton’s law says that the gravitational force is
Gm
1
m
2
/
r
2
, where
G
is Newton’s constant of gravitation,
m
1
and
m
2
are the two masses that are attracted to each other, and
r
is the distance between them.
8
. Newtonian gravity respects Euclidean geometry. In Euclidean geometry,
x
2
+
y
2
+
z
2
, the length of a vector pointing to the point with coordinates (
x
,
y
,
z
), is independent of the coordinate frame. That is, you can rotate your coordinates but the distance to any point won’t change, even though the individual coordinates will. Special relativity puts time into the picture. It says that
x
2
+
y
2
+
z
2
−
c
2
t
2
is independent of your choice of inertial reference frame. Notice that this invariant quantity involves both space and time, but time is treated differently because of the minus sign in front of the term
c
2
t
2
. Also notice that for this quantity to be independent of inertial frame, changes
in reference frame must mix the values of the space and time coordinates. If one reference frame moves at speed
v
with respect to the other in the
x
direction, the transformation of coordinates from (
t
,
x
,
y
,
z
) to (
t?
,
x?
,
y?
,
z?
) would be
x?
γ
x
−
c
βγ
t
,
t?
= γ
t
− βγ
x
/
c
,
y?
=
y
,
z?
=
z
, where β =
v/c
,
c
is the velocity of light, and γ = 1/√(1 − β
2
).
9
. Einstein’s equations tell us how to derive the metric
g
μν
from a known distribution of matter and energy:
R
μν
−½
g
μν
R
= 8π
GT
μν
/c
4
.
R
μν
is the Ricci curvature tensor and is related to the metric
g
μν
,
T
μν
is the stress-energy tensor describing the matter-energy distribution,
G
is Newton’s constant of gravitation, and
c
is the speed of light. For example, for matter of mass density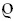 at rest,
at rest,
T
00
=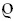 while all the other components of the tensor are 0.
while all the other components of the tensor are 0.
10
. The energy per unit frequency emitted by a blackbody of temperature
T
depends on the frequency,
f
, as
f
3
/(e
hf/kT
− 1), where
k
= 1.3807 × 10
-16
erg K
-1
is Boltzmann’s constant, which converts temperature to energy. Notice that at low frequencies the energy increases with frequency. But at frequencies where the energy of a quantum,
hf
, is large compared with
kT
, the spectrum drastically cuts off; the emitted energy is exponentially smaller at higher frequencies.
11
. A wavefunction is actually a complex-valued function. This is the source of many of quantum mechanics’ strange properties. When you add two complex functions together and then square the sum, you generally get a different result from when you first square and then add. That results in interference phenomena. For example, in the double-slit experiment the probability that is recorded on a screen results from the interference of the waves that describe the electron’s two possible paths.
12
. More precisely, it’s the product of Planck’s constant and the absolute value of the commutator of the two quantities divided by 2.
13
. Special relativity tells us that a stationary object with rest mass
m
0
carries energy
E
=
m
0
c
2
. More generally, an object that is moving with velocity
v
(with β =
v/c
and γ = 1/√(1 − β
2
)) will carry energy
E
= γ
m
0
c
2
. The rest mass is also known as the
invariant mass
(independent of reference frame). That is because, according to the transformation laws of special relativity, the quantity
E
2
−
p
2
c
2
=
m
0
c
4
is the same in any reference frame. Notice that you always need an energy at least equal to
m
0
c
2
to produce an object of mass
m
0
. Also notice that when an object has low mass compared with its energy (really, energy/
c
2
), the energy and momentum are related approximately by
E
=
pc
. That is why, at high energy, energy and momentum are roughly interchangeable.
14
. Maxwell’s Equations (in c.g.s. units) are
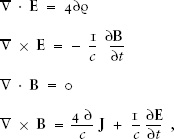
where
E
is the electric field,
B
is the magnetic field,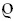 is the charge, and
is the charge, and
J
is the current. These are first-order differential equations; by combining two of them you can derive a second-order differential equation involving only the electric or magnetic field. This equation takes the form of a wave equation—that is, its solutions are sinusoidal waves.
