Warped Passages (35 page)

Notice that if I plot a point at the position
x
= 0,
y
= 0, this
rotational symmetry is completely preserved. But if I plot a point that has one nonzero coordinate value, for example where
x
= 5 and
y
= 0, the rotational symmetry is no longer preserved. The two axes are no longer equivalent because the
x
value, but not the
y
value, of this point is not zero.
19
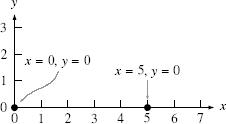
Figure 58.
When the point
x =
0
, y =
0 is singled out, rotational symmetry is preserved. But when
x =
5
, y =
0 is singled out, rotational symmetry is broken.
The Higgs mechanism spontaneously breaks weak force symmetry in a similar fashion. When the two Higgs fields are zero, the symmetry is preserved. But when one is zero and the other is not, the weak force symmetry is spontaneously broken.
The weak gauge boson masses tell us the precise value of the energy at which the weak force symmetry is spontaneously broken. That energy is 250 GeV, the weak scale energy, very close to the masses of the weak gauge bosons, the W
-
, the W
+
and the Z. When particles have energy greater than 250 GeV, interactions occur as if the symmetry is preserved, but when their energy is less than 250 GeV, the symmetry is broken and weak gauge bosons act as if they have mass. With the correct value of the nonvanishing Higgs field, the weak force symmetry is spontaneously broken at the right energy, and the weak gauge bosons get precisely the right mass.
The symmetry transformations that act on the weak gauge bosons also act on quarks and leptons. And it turns out that these transformations won’t leave things the same unless quarks and leptons are massless. That means that weak force symmetries would be preserved only if quarks and leptons didn’t have mass. And because the weak force symmetry is essential at high energies, not only is spontaneous symmetry breaking required for the weak gauge boson masses, it’s neces
sary for the quarks and lepton to acquire masses as well. The Higgs mechanism is the only way for all the massive fundamental particles of the Standard Model to acquire their masses.
The Higgs mechanism functions in exactly the way that is needed to ensure that any theory that incorporates it can have massive weak gauge bosons (as well as massive quarks and leptons) and nonetheless will make the correct predictions for high-energy behavior. Specifically, for high-energy weak gauge bosons—those with energy larger than 250 GeV—symmetry appears to be preserved, so there are no incorrect predictions. At high energies the internal symmetry associated with the weak force still filters out the problematic polarization of the weak gauge boson that would cause interactions at too high a rate. But at low energies, where the mass is essential to reproducing the measured short-range interactions of the weak force, the weak force symmetry is broken.
This is why the Higgs mechanism is so important. No other theory that assigns these masses has these properties. Other approaches fail either at low energies, where the mass will be wrong, or at high energies, where interactions will be predicted incorrectly.
Bonus
There is one more successful feature of the Standard Model that I have not yet explained. Although the Higgs field will be relevant to the next few chapters, this particular aspect of the Higgs mechanism will not. Yet it is so surprising and fascinating that it’s worth mentioning.
The Higgs mechanism tells us about more than just the weak force. Surprisingly, it also gives new insight into why electromagnetism is special. Until the 1960s, no one would have believed that there was more to learn about the electromagnetic force, which had been so well studied and understood for over a century. In the 1960s, however, the electroweak theory proposed by Sheldon Glashow, Steven Weinberg, and Abdus Salam showed that when the universe began its evolution at high temperature and energy, there were three weak gauge bosons, plus a fourth, independent, neutral boson with a different
interaction strength. The photon, ubiquitous and important as it is today, was not a member of this list. The authors of the electroweak theory deduced the nature of the four weak gauge bosons from both mathematical and physical clues, which I won’t go into here.
The remarkable thing is that the photon was originally nothing special. In fact, the photon we talk about today is actually a mixture of two of the original four gauge bosons. The reason that the photon got singled out is that it is the only gauge boson involved in the electroweak force that is impervious to the weak charge of the vacuum. The chief distinguishing feature of the photon is that it travels unfettered through the weakly charged vacuum and therefore has no mass.
Photon travel, unlike that of the W and Z, is not obstructed by the nonzero value of a Higgs field. That’s because although the vacuum carries weak charge, it does not carry electric charge. The photon, which communicates the electromagnetic force, interacts only with electrically charged objects. For this reason, the photon can communicate a long-range force without any interference from the vacuum. It is therefore the only gauge boson that remains massless even in the presence of the nonzero Higgs field.
The situation closely resembles the speed traps with which Ike had to contend (although this part of the analogy is admittedly a little more tenuous). The speed traps let dull cars pass through scot-free. Photons, like the dull neutral cars, always travel unimpeded.
Who would have thought it? The photon, the thing that physicists for years thought they understood completely, has an origin that can be understood only in terms of a more complex theory that combines the weak and electromagnetic forces into a single theory. This theory is therefore generally referred to as the
electroweak theory
, and the relevant symmetry is called
electroweak symmetry
. The electroweak theory and the Higgs mechanism are major successes of particle physics. Not only the weak gauge boson masses, but also the relevance of the photon are neatly explained within its framework. On top of that, it allows us to understand the origin of the quark and lepton masses. The rather abstract ideas we have just encountered nicely explain quite a wide range of features of the world.
Caveat
The Higgs mechanism works beautifully, and gives quarks, leptons, and weak gauge bosons their masses without making nonsensical high-energy predictions—and, furthermore, explains how the photon came to be. However, there is one essential property of the Higgs particle that physicists don’t yet fully understand.
Electroweak symmetry must be broken at about 250 GeV to give particles their measured masses. Experiments show that particles with energy greater than 250 GeV look as if they are massless, whereas particles with energy below 250 GeV act as if they have mass. However, the electroweak symmetry will break at 250 GeV only if the Higgs particle (sometimes also called the Higgs boson)
20
itself has roughly this mass (again, using
E
=
mc
2
); the theory of the weak force wouldn’t work if the Higgs mass were much greater. If the Higgs mass were greater, symmetry breaking would happen at a higher energy and the weak gauge bosons would be heavier—contradicting experimental results.
However, in Chapter 12, I will explain why a light Higgs particle poses a major theoretical problem. Calculations that take quantum mechanics into account point to a heavier Higgs particle, and physicists don’t yet know why the Higgs particle mass should be so low. This quandary is critical to motivating new particle physics ideas and some of the extra-dimensional models that we’ll consider later on.
Even without knowing the precise nature of the Higgs particle and the reason why it is so light, the mass requirement tells us that the Large Hadron Collider, which will start operating at CERN in Switzerland within the decade, should discover one or more crucial new particles. Whatever breaks electroweak symmetry must have a mass that is around the weak scale mass. And we expect that the LHC will find out what it is. When it does, this critically important discovery will greatly advance our knowledge of the underlying structure of matter. And it will also tell us which (if any) of the proposals for explaining the Higgs particle is correct.
But before we get to those proposals, we’ll look at one possible extension of the Standard Model that was suggested purely in the
interest of simplicity of nature. The next chapter explores virtual particles, the distance dependence of forces, and the fascinating topic of
grand unification
.
What to Remember
- Despite the importance of symmetries for making the right predictions about high-energy particles, the masses of quarks, leptons, and weak gauge bosons tell us that the
weak force symmetry
must be broken. - Because we still have to guard against false predictions, the weak force symmetry must nonetheless be maintained at high energy. Therefore, the weak force symmetry must be broken only at low energy.
- Spontaneous symmetry breaking
occurs when all physical laws preserve a symmetry but the actual physical system does not. Spontaneously broken symmetries are symmetries that are preserved at high energies but broken at low energies. The weak force symmetry is spontaneously broken. - The process by which weak force symmetry is spontaneously broken is the
Higgs mechanism
. For the Higgs mechanism to spontaneously break the weak force symmetry, there has to be a particle with a mass of about the weak scale mass, which is 250 GeV (remember, special relativity relates energy and mass through
E
=
mc
2
).
Scaling and Grand Unification: Relating Interactions at Different Lengths and Energies
I hope someday you’ll join us
And the world will live as one.
John Lennon
Athena often felt like she was the last to be told anything interesting. She didn’t even hear about Ike’s adventures with his car until after he had owned it for over a month. And she didn’t learn them from him directly—she learned about them from a friend of hers who had heard about them from Dieter’s cousin’s brother, who had learned about them from Dieter’s cousin, who had heard about them from Dieter.
Through this indirect route, Athena was told Ike’s remark, “The influence of forces depends on where you are.” Ike’s uncharacteristic pronouncement completely mystified Athena until she realized that the message must have been distorted along the way. After thinking about it awhile, she decided that Ike’s real remark must have been, “The performance of Porsches depends on the model of car.”
We’ll see that the statement Athena originally heard is true. This chapter is about how physical processes that take place between particles at one separation can be related to those that take place at another separation and why physical quantities, such as a particle’s mass or interaction strength, depend on the particle’s energy. This dependence on energy and distance is over and above the classical separation dependence of forces. For example, classically, the strength
of electromagnetism, like that of gravity, decreases in proportion to the square of the interacting objects’ separation (the inverse square law). But quantum mechanics changes this distance dependence by influencing the strength of the interaction itself so that particles at different separations (and energies) seem to interact with different charges.
Forces become weaker or stronger with increasing distance as a result of
virtual particles
—short-lived particles that exist as a consequence of quantum mechanics and the uncertainty principle. Virtual particles interact with gauge bosons and alter forces so that their effect depends on distance, much as Athena’s friends distorted Ike’s message as they passed it along.
Quantum field theory tells us how to compute the effect of virtual particles on the distance and energy dependence of forces. One triumph of such calculations was that they explained why the strong force is so strong. Another interesting fallout was the potential existence of a
Grand Unified Theory
, in which the three nongravitational forces, which are so different at low energies, merge into a single unified force at high energies. We’ll explore both of these results and the quantum field theory ideas and calculations that underlie them.
When you are reading the next few chapters, bear in mind the very disparate energy scales we are discussing. The unification energy is about one thousand trillion GeV, and the Planck scale energy, where gravity gets strong, is about a thousand times greater than that. The weak scale energy, which is the energy where experiments currently operate, is a whole lot smaller: it is only about a hundred to a thousand GeV. The weak scale energy is about as small relative to the unification energy as a marble’s size is compared with the distance between the Earth and the Sun. I’ll therefore sometimes call the weak scale energy low even though it’s a high energy from the perspective of experiments,
*
as it’s so much smaller than both the unification and the Planck scale energies.
