The Unimaginable Mathematics of Borges' Library of Babel (7 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

Our new
twist on these calculations involves what Hurley translates as the
"letters on the front cover of each book." For the sake of precision,
we note that the Spanish reads "el dorso de cada libro," which
translates literally as "the back of the book." Idiomatically and
bibliographically, however, the sense of this phrase is that the letters are on
the
spine
of the Library's books. As such, the interpretation we use for
the rest of this book is that the letters are on the spine.
Now, the
number 25
1,312,000
we calculated above doesn't account for these spinal letters. It
strikes us as likely that, within the imaginary universe of the Library, a book
with the letters
The Plaster Cramp
written on the spine, whose 1,312,000
slots are filled by the repeated sequence of orthographic symbols MCV, should
be considered as a book distinct from one with the exact same pages which is
instead imprinted with the letters
Axaxaxas Mlö
on the spine.
2
Scanning through the original
Spanish version, "La biblioteca de Babel," we find a book described
with the 19 orthographic symbols
El calambre de yeso
on its spine. This
means that there are a minimum of 19 slots to fill on each spine, and
accounting for these variations with repetition expands the Library by a factor
of
at least
25
19
= 363,797,880,709,171,295,166,015,625.
We write this number out
explicitly to re-echo the vastness of the numbers woven through the Library.
Simply adding 19 orthographic symbols on the spine magnifies the Library more
than 300 septillion times. For comparison, this number is roughly the number of
microscopic plant cells comprising a grove of 364 oak trees.
3
So if the Library of 25
1,312,000
books is considered as
one
imperceptible plant cell, accounting for differing symbols on the spine
multiplies the Library into a
grove
of 364 giant oak trees.
However,
since we cannot be sure of either the maximum number of symbols on the spine of
each book or of Borges' intent, we restrict ourselves to 25
1,312,000
books. This number, so easy to write, is, in a powerful sense, utterly
unimaginable. To see that we can't see it, let's begin by converting this
number to a
power of 10,
which puts it in a more familiar context.
25
1,312,000
is just a little bit larger than 10
1,834,097
;
which is, of course, a 1
followed by one million, eight hundred thirty-four thousand, and ninety-seven
0s. We accomplish this conversion to a power of 10 notation using the
logarithmic
function and discuss the mechanics in the Math Aftermath
portion of this chapter.

Could our universe possibly
contain the Library? Current research approximates the size of the universe as
being about 1.5 x 10
26
meters across. Let's simplify calculations
and create an upper bound to the universe by overestimating its size and
supposing that our universe is shaped like a cube, each side of which measures
10
27
meters (figure 3).
So, we'll
say that our cubic universe consists of approximately 10
27
∙ 10
27
∙ 10
27
= 10
81
cubic meters. If we assume that we may fit
1,000 = 10
3
Library books in a cubic meter—and this is an
exceedingly generous assumption—then our universe, if it consisted of
nothing
except books, would contain
10
81 10
10
3
= 10
84
books.
This doesn't make the
slightest dent in the Library; it would take
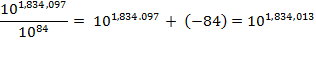
universes the size of ours to
hold just the books of the Library. What if the books were each as small as a
grain of sand?
Using a
ruler shows that an average grain of sand is approximately one millimeter
across. If we assume a cubical shape combined with a perfect packing, then we
could fit approximately
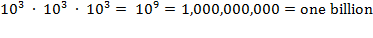
grain-of-sand books in a cubic
meter. Multiplying by the size of the universe, we find that the universe holds
only
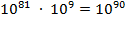 such books.
such books.
That is, if the universe
consisted of nothing but sand, it would hold at most about 10
90
grains of sand. As we promised at the beginning of the chapter, using
exponential notation allows us to estimate the number of grains of sand
considerably faster than Archimedes.
Once again,
though, this hardly impacts the Library's collection. As a final illustration
of this point, suppose that each book is shrunk to the size of a proton; that
is, shrunk to about 10
-15
meters across. Given that each book is 10
-15
meters across, we could pack 10
15
of them in a very narrow
one-meter-long strip. Thus, packing a cubic meter with proton-sized books
yields
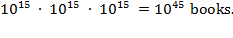
Our universe holds merely
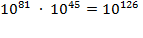 of these subatomic books.
of these subatomic books.
Let's adopt one more viewpoint
in our efforts to conceptualize the enormity and complexity of the Library. Perhaps
the simplest books to imagine, of which there are exactly 25, are those that
consist of nothing except one symbol, repeated for the entire book. For
example, one such book would consist of its 1,312,000 slots filled by the
letter
g
.
4
The
first two lines of that book would read
gggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg
gggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg
and so on
for another 38 lines on the first page, followed by 40 more lines on each of
the remaining 409 pages: a veritable rhapsody in
g
.
Now allow a
slight variation. The next set of books we consider are those that consist of
entirely the orthographic symbol
g
except for one
h
. That is, exactly
1,311,999 slots will be filled with the letter
g,
while exactly one slot
will contain the letter
h
. One such book will begin
gggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggggg
