The Unimaginable Mathematics of Borges' Library of Babel (5 page)

WE BEGIN WITH A PAEAN TO
THE MODERN
method of denoting numbers,
especially the convention of exponential notation, employed first by Descartes
in 1637, then extended over the next few decades, primarily by Napier and
Newton. (These days, it's commonly also called scientific notation.) In one of
his most famous works, Archimedes, a singularly brilliant intellect of the
classical world, needed approximately 12 pages (in English translation) to
create names of numbers and methods of multiplication to produce an
upper bound
—a
maximal estimate, a cap—on the number of grains of sand in the world. By using
modern notation, particularly the idea of the exponential, it will take us less
than one paragraph to produce an upper bound on the number of grains of sand in
the
universe.
Furthermore, in short order these exponential conventions
confer the power to accomplish a task that might well have stymied Archimedes:
calculating the precise number of distinct books in the Library

A positive
integer
exponent
signifies, "the amount of times some number is
multiplied by itself." For example,

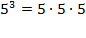 and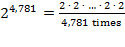
.

are concise ways to express a
"small" number

.

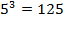and a very large number.
^*
 There are only two rules
regarding the manipulation of exponentials that concern us. The first:

Rule 1:
Multiplying numbers written in exponential notation is equivalent
to adding the exponents.

For example:

.

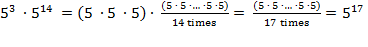The second rule nicely
complements the first.

Rule 2:
Dividing numbers written in exponential notation is equivalent to
subtracting the denominator's exponent from the numerator's.

For example:

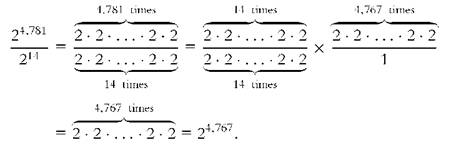
The second rule leads to the
useful convention of using a
negative
exponent to represent a power in
the denominator, for instance,

.

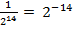Thus the previous example may
concisely be written

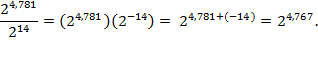
It is remarkable that such
relatively simple notation can transform relatively complicated tasks,
multiplication and division, into the relatively easy and intuitive
computations of addition and subtraction.

While
pondering previous critical responses to "The Library of Babel," we
discovered that a number of people either calculated the number of books or
gave some indication of how one might go about it.
¹
Our intent in providing the lightning review of exponential
notation is to demystify the calculation, and then, more importantly, to give a
sense of the enormity of the Library. Then, after the calculation, we tease out
a previously overlooked detail from the story and use it to set a new lower
bound on the number of books in the Library. (For us, a
lower bound
will
be number that says, "We guarantee that
there are at least this many
books in the Library.")

For the
purposes of this book,
combinatorics
is the branch of mathematics that
counts the number of ways objects can be combined or ordered. Before using
combinatorics to calculate the number of the books, let's consider 10 familiar
orthographic objects, the symbols we use as representations for digits: 3, 8,
9, 1, 6, 2, 0, 5, 7, 4. We deliberately disordered them to help you see them
not as you usually do, as
numbers,
but rather as symbolic
representatives of the numbers 0 through 9.

Using these
symbols, we'd like to occupy exactly one slot with one symbol, and so we ask:
how many distinct ways can we fill one slot? Hopefully, the answer is
clear—there are 10 ways to fill one slot with one of the symbols.

1. 0

2. 1

3. 2

4. 3

5. 4

6. 5

7. 6

8. 7

9. 8

10. 9

Now, how many distinct ways
are there to fill
two
slots, such that each slot contains one symbol?
One complete list of answers, ordered in a familiar way, reads: 00, 01, 02, 03,
... , 97, 98, 99. So we see that there are 100 ways to fill the two slots, given
that each slot contains one symbol and that repetition is allowed (enabling
such combinations as 00, 11, 22, 33, etc.). Deliberately blurring the
distinction between the orthographic symbols and the numbers they represent, we
note that there are

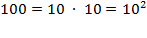
ways to fill the two slots. If
we ask how many distinct ways there are to fill
three
slots, such that
repetition is allowed and each slot contains one symbol, we generalize our work
from above and produce a complete list that reads: 000, 001, 002, 003,..., 99Z,
998, 999. This time, we see that there are 1,000 ways to fill the three slots.
Continuing to blur the distinction between the orthographic symbols and the
numbers they represent, it follows that there are