The Unimaginable Mathematics of Borges' Library of Babel (29 page)

even though they are not
integers?" One tempting possible answer for the latter question is to
focus on the "keep multiplying by numbers reduced in size by subtracting
one" aspect of the factorial, and define, for example,

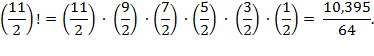
Instead, in 1729, a similar
yet more encompassing route was discovered by Leonhard Euler. Euler used the
integral calculus to define a new function, called the
gamma function,
which, like the logarithm, possesses many interesting properties. One is that
if a positive integer
n
is input to the gamma function, then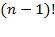
 is the output, meaning that the gamma function is essentially a
generalization of the factorial. We test our naïve guess by inputting 13/2 to
the gamma function, and find that the output is, in fact, pretty close:

At any rate, factorial
notation shares a property with exponential notation: it is easy to write down
unimaginably large numbers. Take, for example, the number 70!, which by virtue
of the simplicity of its written form appears as though it should fall within
the grasp of the human imagination. In reality, 70! is larger than 10
¹⁰⁰
,
and as we saw in the chapter "Combinatorics," 10
¹⁰⁰
grains
of sand would completely fill 10 billion universes the size of our own.

Now, in the
sort of action standard for a mathematician that incurs withering scorn from
engineers, we accomplish the impossible by simply asserting it as a fact:
number all the book-sized slots in the bookcases in the Library from 1 to 25
^1,312,000
.
(Wasn't that easy?) Via this numbering of the spaces in the bookshelves, we may
use the factorial to compute the number of different ways to order the books in
the Library Even though the numbering of the slots in bookcases in the Library
necessarily twists and snakes through three dimensions, we can still regard it
as a consecutive sequence of 25
^1,312,000
slots laid out in a row.
Put another way, regardless of how they are distributed in space, the positive
integers have an intrinsic linear ordering, given by the progression 1, 2, 3,
etc.

Given that
each specific book fills a particular numbered slot, armed with the factorial
notation we may trivially write down the number of different ways that the
books in the Library may be shelved. Considering each book as a distinct
object, there are

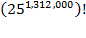
different orderings. We'd like
to get a sense of the magnitude of this number; after all, a factorial as small
as 70! taxes our power of visualization by easily exceeding the number of
subatomic particles in our universe. Fortunately,
Stirling's approximation
to the factorial
gives a good estimation, in the sense that we can see this
gargantuan number as an exponential of 10.

Stirling's
approximation applied to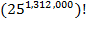
 yields
.

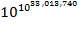This says that the number of
different orderings of the books in the Library is approximately a
33-million-digit number; in the context of the story, it would take about 26
volumes simply to write down the number. The upshot is that Builders may
construct a finite-sized Library housing all possible orderings of the books by
assembling (25
^1,312,000
)! Library-sized and -shaped buildings,
filling each such building with exactly one ordering of the books.

If, though,
along with the librarian, we assume that the Library is infinite in all
directions, we have ample space for a more ambitious scheme than simply
accounting for all orderings. We'll begin by defining a
libit
as a
contiguous collection of accessible hexagons holding one particular ordering of
the 25
^1,312,000
distinct books of the Library—any shape of the libit
is acceptable so long as Euclidean 3-space can be completely
tiled
by
replicas of that shape. Although we are imagining a libit looking roughly cubic
or almost like a hexagonal prism, here's an extreme example unlike those: a
tower of stacked single hexagons sufficient to hold all the distinct books.
Here's another: a giant near-hexagon of hexagons completely contained on one
floor, again sufficiently large to hold all the distinct books.

Next, tile
all of 3-space by clones of the libit, and from the infinite possibilities,
arbitrarily choose an initial libit and also any hexagon contained within.
We'll use this hexagon as a reference point, and consider it to be the origin
of the Library. Starting at the origin, successively choose contiguous hexagons
in an orderly fashion until the first libit is completely numbered. (It is not
unreasonable to worry about how to ensure that every hexagon will be numbered.
We address this issue in the chapter "Critical Points.")

Now choose
an adjacent libit, and starting in the "same" hexagon as in the first
libit—that is, in the hexagon in the second libit that corresponds to the
origin—extend the numbering starting with 25
^1,312,000
+ 1. The
numbering of the second libit will, of course, run all the way up to 2
  (25
^1,312,000
). Next, repeat the process by choosing a
third libit contiguous to the second one, and number the slots on the shelves
as before.

Continue to
iterate the procedure until the shelves in (25
^1,312,000
)! contiguous
libits are numbered, and note that each of the (25
^1,312,000
)!
different orderings is composed of 25
^1,312,000
different books.
Thus, for the first step of the Grand Pattern, we utilize the first

25
^1,312,000
x
(25
^1,312,000
)!

=
(Number of distinct books)
x
(Number of distinct orderings)

slots in the infinite Library.

However, as
we were filling the libits with different orderings, we were implicitly making
choices regarding the possible orderings of the books. Making the Grand Pattern
requires us to leap categories and consider orderings of orders. Let's do a
smaller-scale example of a Grand Pattern constructed in the Euclidean plane.