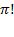The Unimaginable Mathematics of Borges' Library of Babel (28 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

Let us now
rejoin our librarians, at the moment after their "stark and depressing
conclusion."
It was as if
our minds, mocking our exhausted, rooted, dispirited bodies, were set free.
Almost in opposition to our wills, without fully digesting the realization, we
continued to ruminate on these matters. One of us— does it matter
which?—invoked a fragment in a contentious book found on a lower level, that
read in part,
Imagine a
narrow flexible tube, one thousand miles long, called a "garden
hose," laid out flat on a gigantic floor so that the hose impeccably fills
the floor. The hose may curve abruptly, swirl painfully, spiral exuberantly,
loop discursively, or even run straight, but it may never cross over itself nor
rise from the ground in any way. Perhaps at many points the hose makes a kind
of moral cusp or treacherous eddy and the close-by exterior parts of the tube
nestle next to nearby parts of the tube. Skywards down to the hose, the view of
the godlike will pinpoint many spots where the hose appears as parallel strands
lying next to each other. At those spots, an ant—a tiny six-legged librarian—
crawling through the interior of the hose may travel a considerable distance,
perhaps miles, to reach a contiguous section. Even worse, never mind the Origin
of the ant: the more it crawls, the more places it finds where the walls of the
hose keep it further and further away from places the godlike can see. Lament,
therefore, the linear forwards-and-backwards motion of the ant inside, while
the nonlinear arabesques of the exterior hose bring grace and redemption to those
who can read them. Never shall the ant crawl from the interior and gaze upon
the wholeness of the hose.
Paralyzed, we saw that
although our limbs numbered four, and despite the fact that we weren't trapped
in such a strange loop, there were striking similarities between the situation
for the ants and for us. Regardless of the clever patterns taken by a godlike
being laying down the garden hose, there must ever be more spots where the
long, slimber structure of the loops of the hose would thwart an ant's attempt
to move to any point athwart of the hose besides those immediately forwards or
directly backwards. Clenching the hose into a crimp and then twisting it around
in a whirlpool will produce a section where the ant could easily travel to all
spots near its starting point, but then as the hose continues to be laid down,
filling out the floor, circling around and again in a dizzying whorl of a world
for the ant... we simply stopped talking, exhausted, looking up and down the
airshafts.
Our
Conjecture of Extreme Disconsolation:
There
are unimaginably vast numbers of pairs of adjacent hexagons such that the span
of our combined lives would not suffice to travel from the one to the other.
Our earlier impotence was now
seen to be a dream; our true plight lay revealed: perhaps we inhabited a
section of the Library where all or most hexagons would allow us to attain only
two of the six adjacent hexagons. All of those books, perhaps my or my friend's
Vindication, perhaps a grammar of an ideal logic capable of straightening out
the labyrinth in which we found ourselves, perhaps a fitting valediction for a
carelessly dropped book mournfully hurtling down an airshaft, all these books
would never be read by us.
More Combinatorics
Disorderings into Order
There is a secret element
of regularity in the object which corresponds to a secret element of regularity
in the subject.
—Johann
Wolfgang von Goethe,
Maxims and Reflections
Thinking man has a strange
trait: when faced with an unsolved problem he likes to concoct a fantastic
mental image, one he can never escape, even when the problem is solved and the
truth revealed.
—Johann
Wolfgang von Goethe,
Maxims and Reflections
Either a universe that is
all order, or else a farrago thrown together at random yet somehow forming a
universe. But can there be some measure of order subsisting in yourself, and at
the same time disorder in the greater whole?
—Marcus
Aurelius,
Meditations
 CALCULATING THE NUMBER OF DISTINCT BOOKS
CALCULATING THE NUMBER OF DISTINCT BOOKS
in the Library, as seen in "Combinatorics: Contemplating
Variations of the 23 Letters," is an example of a straightforward problem
with a tidy solution. In this chapter, we do not so much solve a problem as
explore how a maximally disordered and chaotic distribution of books in the
Library can be seen as a Grand Pattern. This work is grounded in ancient ideas
of combinatorial analysis, and although the ideas are consistent with the
structure of the story, the ordering of the books we outline is incompatible
with the Librarian's "elegant hope" that
If an eternal
traveler should journey in any direction, he would find after untold centuries
that the same volumes are repeated in the same disorder—which, repeated,
becomes order: the Order.
The Order conjectured by the
librarian is an iterative order; a two-dimensional analogue may help to
visualize it. Think of the complete ordering of all the books as being given by
the imprint of a rubber stamp. After making an initial stamp (the section of
the Library that the librarian lives in), without rotating the stamp at all and
without overlapping stamps, continue applying the stamp up and down, left and
right, and eventually cover the piece of paper. This translates the original
order in all directions, vertically and horizontally, forming a simple kind of
symmetry
The Grand
Pattern we propose in lieu of the Librarian's iterative Order is, in some
sense, an ever-growing chain of concatenations of
all possible orderings.
To help envision what we mean, imagine that the Library is finite and
approximately in the shape of a cube. Suppose we adjoined another Library-sized
and Library-shaped building to the first one and distributed the 25
1,312,000
unique books in a different ordering. This surely violates the Librarian's
elegant hope, for it contradicts his vision that the addition should contain
the books in precisely the same order as the original section. Now, suppose we
continue to extend the Library by adjoining Library-sized and Library-shaped
structures, each time distributing the books in a new ordering. Our endeavor
now is to formalize the process, being as disorderly as possible, and at the
end of a piece-by-piece construction, find an infinitely sized Library with a
Grand Pattern occupying the whole of Euclidean 3-space.
Let's begin
with a relatively simple question: how many distinct linear orderings are there
of the three objects {
▲, █, ●
} such that each object appears exactly once? A few moments of
work produces the following list:
1.
▲, █, ●
2.
▲, ●, █
3.
█, ▲, ●
4.
█, ●, ▲
5.
●, ▲, █
6.
●, █, ▲
How might we convince
ourselves that the list exhausts all possibilities? Perhaps by noting that we
can fill the first slot three different ways, with either
▲, █, or ●
.

Once the first slot is filled,
we are left with exactly two objects and two slots. Either of the two remaining
objects can fill the second slot: we have two choices. Then, whichever object
is left must fill the last slot. In other words, there are six different ways
to fill the slots (figure 61).
Since the
list has six distinct entries, we may be sure we've exhausted all
possibilities. Generalizing this line of thinking, if we have four objects,
there will be
4
x
3
x
2
x
1=24
distinct ways to arrange the
four objects: four choices for the first slot, three for the second slot, two
for the third slot, and only one object remaining to fill the last slot.
Explicitly
writing out the multiplications is viable for a relatively small number of
objects. However, if we wished to signify the integer corresponding to the
number of different ways to order only 25 objects, we'd find it cumbersome.
Fortunately, a snappy notation, that of the
factorial,
was developed in
the early 1800s:
1! = 1
2! = 2
x
1=2
3! = 3
x
2
x
1=6
4! = 4
x
3
x
2
x
1=24
.
.
.
25! = 25
x
24
x
23
x … x
3
x
2
x
1
.
.
.
n! = n
x
(n - 1)
x
(n - 2)
x … x
3
x
2
x
1.
The orthographic symbol
"3!" is read and pronounced as "three factorial," where
"factorial" is understood to represent the process of multiplying an
initial integer by every positive integer smaller than itself.
Several
observations about factorials. First, on a personal note, even after 25 years
of the serious study of mathematics we still tend to read "3!" as
"THREE!" (very excitedly). Second, although we won't use the answers
in this work, some natural questions to ask are "How is 0! defined?"
and "Can we make sense of the expressions
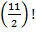 or
or