The Unimaginable Mathematics of Borges' Library of Babel (35 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

The problem is much worse in
higher dimensions. The example of the Fibonacci sequence is one-dimensional;
now let's look at one example of the "guessing-of-terms" problem in a
two-dimensional setting. The numbers in the hexagonal array pictured in figure
69 are the first seven terms of the Fibonacci sequence, and let's imagine that
all the digits to fill out the plane are exactly those appearing in the
Fibonacci sequence. But how are the next twelve terms to be ordered? Your guess
is as good as mine: There are a vast number of distribution rules utilizing the
Fibonacci digits which would produce the pictured hexagonal array. Now imagine
a librarian's dilemma, confronting 410-page collections of seemingly random
lexical symbols—not even numbers—distributed in some sort of
three-dimensional
lattice. The mind balks at conceiving of any rule to
order the books.
A final pair
of observations that fit this chapter best. First, Borges introduces the belief
of the Book-Man.
We also have
knowledge of another superstition from that period: belief in what was termed
the Book-Man. On some shelf in some hexagon, it was argued, there must exist a
book that is the cipher and perfect compendium
of all other books,
and
some librarian must have examined that book; this librarian is analogous to a
god.
A cipher is either a key or a
code, and a compendium is, according to various dictionaries, a brief, a
condensation, an epitome, or an abstract. My guess is that Borges meant that
since it is possible to conceive of a book 410 pages in length that is a key to
and an abridgement of the Library, that book must therefore exist in the
Library. Such a book might, in today's parlance, be a computer algorithm for
generating all possible symbol sequences of length 1,312,000 from an alphabet
of 25 orthographic symbols, for such an algorithm could actually be written in
just a few lines of code. More of the Book might be devoted to the generating
principles and topology of the Library; possibly a rule for ordering the books
(although probably no such rule could fit in one volume); the motivations of
the constructors of the Library; how the Library was built and where the
materials for it came from; how librarians entered the system; etc. etc. Since
such a book can be conceived, the import of Borges' footnote is precisely that
it must appear in the Library. Of course, its refutations also exist in the
Library, a fact that highlights and compounds the problem of interpretation of
truth.
Second, many
critics, including some of those mentioned here, have speculated about the
meaning and significance of one of Borges' parenthetical asides in the story:
(Mystics
claim that their ecstasies reveal to them a circular chamber containing an
enormous circular book with a continuous spine that goes completely around the
walls. But their testimony is suspect, their words, obscure. That cyclical book
is God.)
I won't presume to provide an
exegesis of the cyclical book, but I offer the following insight for a future
critic who might wish to interpret it: I believe that again Borges is winking
at the reader.
It would be
impossible to remove such a book from the shelf!
The only way to read the book
would be to physically cut out sections; in other words, the only way for the
mystics to attain the Book that is God would be to destroy It. The Book is
closed (figure 70).

Openings
To open a book brings
profit.
—Chinese
proverb
 IN THIS CHAPTER, I ASSEMBLE
IN THIS CHAPTER, I ASSEMBLE
SOME FACTS FOR THE
purpose of sketching a
picture of the mathematics Borges may have known and how it may have affected
the story In his prologue to the first part of
Ficciones,
Borges winks
yet again at the reader when he writes "I am not the first author of the
narrative titled 'The Library of Babel'; those curious to know its history and
its prehistory may interrogate a certain page of Number 59 of the journal
Sur,
which records the heterogenous names of Leucippus and Lasswitz, of
Lewis Carroll and Aristotle." This is precisely the issue of
Sur
in
which his essay "The Total Library" appears.
1
Perhaps few
others have had the patience to ferret out the particulars of a hint of Borges'
knowledge of combinatorics. Borges opens the story with the following fragment
from Burton's
The Anatomy of Melancholy:
"By this art you may
contemplate the variation of the 23 letters. . ." The entire section of
Burton is concerned with ways of diverting and amusing oneself, ostensibly
towards the end of avoiding or curing melancholy.
2
For several pages before the excerpt, Burton waxes erudite on the
pleasures of reading, especially scripture, and of libraries. Without even a
paragraph break to ease the transition, Burton moves to pleasures mathematical
(emphasis added):
art of
memory, Cosmus Rosselius, Pet. Ravennas, Scenkelius's Detectus, or practise
Brachygraphy, &c., that will ask a great deal of attention; or let him
demonstrate a proposition in Euclid, in his last five books, extract a square
root, or study Algebra; than which, as Clavius holds, "in all human
disciplines nothing can be more excellent and pleasant, so abstruse and
recondite, so bewitching, so miraculous, so ravishing, so easy withal and full
of delight,"
omnem humanum captum superare videtur.
By this means
you may define
ex ungue leonem,
as the diverb is, by his thumb alone the
bigness of Hercules, or the true dimensions of the great Colossus, Solomon's
temple, and Domitian's amphitheatre out of a little part.
By this art you
may contemplate the variation of the twenty-three letters, which may be so
infinitely varied, that the words complicated and deduced thence will not be
contained within the compass of the firmament; ten words may be varied 40,320
several ways;
by this art you may examine how many men may stand one by
another in the whole superficies of the earth .. .
It's worth mentioning that the
number of distinct ways to order eight words is
8!
= 40,320.
Perhaps Burton had neither the
skill nor the stomach to continue multiplying 40,320 by 9 and then again by 10,
which would yield 3,628,800, the number of different ways to order 10 words.
Whether or not Borges would have recognized this number is moot, yet in his
1936 essay "The Doctrine of Cycles," he correctly calculates the
number of ways that the order of 10 atoms can be permuted.
Regardless,
he was aware that the passage alluded to combinations and permutations, and
that "the words complicated and deduced thence will not be contained
within the compass of the firmament." Later in the story, Borges' use of
the phrase "the rudiments of combinatory analysis, illustrated with
examples of endlessly repeating variations" shows that Borges understood
the ideas well, even if a modern mathematician would more likely employ the
phrase "variations with unlimited repetition."
Beyond
gleaning the story and
Selected Non-Fictions
for clues about his
knowledge and predilections, I was fortunate to find another source of
information. The chapter title, "Openings," stems from an
intersection of optimism and pseudo-randomness. While visiting the National
Library of Argentina, I had the great pleasure of perusing the math and science
books Borges donated to the collection. I applied the principle that a book
beloved by its owner, when held gently underneath the spine and allowed to fall
open, will naturally reveal an oft-consulted page. My excitement at achieving
interesting results was matched by my chagrin when, after multiple applications
of this "opening" principle, I discovered that Borges marked the back
end leaves of his volumes with his name, the year of acquisition, and the page
numbers—coupled with a succinct phrase—of passages that especially interested
him. My chagrin was tempered by the fact that his annotated page numbers
unmistakably corresponded with my optimistic openings.
I'll begin
with a book that postdates "The Library of Babel," one that evinces
that Borges hadn't lost interest in the idea of the Library. In 1949, Borges
acquired Russell's
Human Knowledge: Its Scope and Limits.
One of his
three annotations on the end leaf is "Eddington's monkeys." Here is
the passage from page 484 (emphasis added):
Eddington
used to suggest as a logical possibility that perhaps all the books in the
British Museum had been produced accidentally by monkeys playing with
typewriters.
3
There
are here two kinds of improbability: in the first place some of the books in
the British Museum make sense, whereas the monkeys might have been expected to
produce only nonsense [.. . ] Suppose you have in your hands two copies of the
same book, and suppose you are considering the hypothesis that the identity
between them is due to chance: the chance that the first letter in the two
books will be the same is one in twenty-six, so is the chance that the second
letter will be the same, and so on.
Consequently the chance that all the
letters will be the same in two copies of a book of 700,000 letters is the
700,000th power of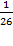 .
.
Russell derives a viewpoint
complementary to that of the Library. If there are 700,000 letters per book and
an alphabet of 26 letters, then the total number of books is 26
700,000
.
Therefore, the probability of picking a book that exactly matches another is
one in 26
700,000
; that is