The Unimaginable Mathematics of Borges' Library of Babel (38 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

 ,
,
and taking the square root of
both sides of the equation yields
 .
.

In fact, it follows instantly
that if
h
is the length of the hypotenuse, then Pythagoras implies
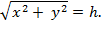
Thus the key point is the
realization that the length of the hypotenuse is expressible in this form. Now,
think of the bottom-left point of the hypotenuse as the origin (0, 0) of the
plane and reimagine the lengths of the legs,
x
and
y,
as
representing the horizontal and vertical coordinates for the right-top point of
the hypotenuse. Then the length of the hypotenuse signifies the distance from
the origin to the point
p
= (
x
,
y
), and applying the
Pythagorean theorem reveals the distance to be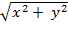 . See figure 72.
. See figure 72.
Now, we want
to use these ideas in order to derive an equation equivalent to Euclid's
intuitively satisfying definition of a circle. He defined a circle to be the
set of points in a plane that are equidistant from a given point. If we set the
given point to be the origin, and choose the distance to be equal to one, then
a circle is the set of all points (x, y) that satisfy the equation.

After squaring both sides, we
see that it must be the case that a unit circle is precisely all points
(
x,
y
) that fit this equation:
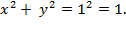


This is how the analytic
equation for the circle arises, and figure 73 indicates a way of viewing a
circle as a composition of distances from the origin, that is, as hypotenuses
of right triangles.
The equation
for a 2-sphere is very similar in concept, and thus we need only adapt our
notion of distance—and therefore, the Pythagorean theorem—to work in
three-dimensional space. A standard way is a typically incisive mathematical
maneuver which requires the clever use of the Pythagorean theorem twice.
To see this,
let's find the distance from the origin (0, 0, 0} to the point
p
= (
x
,
y, z
) in coordinatized 3-space. The point
p
naturally determines a
right triangle, with the first leg of the triangle being the line segment
contained in the
x
-
y
plane (for which
z
= 0} that
connects the origin to the point (
x
,
y
, 0}. The second leg is the
vertical line segment connecting the points
p
and (
x
,
y
,
0}. The hypotenuse of this right triangle is the distance we want—see figure
74.
Observe that
the length of the leg that connects
p
to the point (
x
,
y
,
0) is simply the height, z. Since the other leg is contained in the
x
-
y
plane for which
z
is constantly 0, at a critical juncture below we will
ignore the
z
coordinate and blithely apply the Pythagorean theorem as we
did above in the Euclidean plane. First, though, using the Pythagorean theorem
on the dark gray triangle in figure 74 gives


