The Unimaginable Mathematics of Borges' Library of Babel (30 page)

Instead of books, we'll use
the three letters {a, b, c}. In Step 1, we give a straightforward ordering of
the three letters, which, by analogy, is similar to using books to fill the
first libit. For Step 2, we produce one list of the 3! = 6 possible orderings
of the three letters, and we think of this as the set of (25
^1,312,000
)!
libits described above (figure 62). Next, note that there are 6! = 720 distinct
lists of six orderings. This is exactly the idea we want to communicate: that
although we ran through all possible orderings in the list of six, if we think
of each of the six orderings as a new unit there are 720 orderings which must
be accounted for in Step 3. Put another way, first we worried about all the
ways to order {a, b, c}. Now, we want all possible orderings of

{[a,
b, c]; [a, c, b]; [b, a, c]; [b, c, a]; [c, a, b]; [c, b, a]}.

Figure 63 shows five distinct
lists, beginning a spiral, which ultimately creates a new, larger rectangle
filled out by all 720 distinct 3
x
6 rectangles. This, in turn, is an ordering of orderings of
orderings and guarantees that at the next stage, Step 4, we'll be able to
continue to spiral around and create an even larger rectangle.

Now, let's
move out of the plane, return to the Library, and apply these ideas to create
the Grand Pattern there. At the conclusion of the first step, we went on hiatus
having filled (25
^1,312,000
)! libits, each representing an ordering
of the Library. Now we boldly expand the Library until there are

((
25
^1,312,000
)
!
)
!

libits, each one representing
a distinct ordering of distinct orderings. In other words, this second step of
the Grand Pattern subsumes the first step as just
one
particular
ordering of all orderings of the books of the Library.

And now the
iterative process grows clear; the third step of the Grand Pattern must account
for all orderings of all orderings of all orderings of the books in the Library
There are

(((25
^1,312,000
)!)!)!

such orderings. The third step
of the Grand Pattern subsumes the second step as just
one
particular
ordering of all orderings of all orderings of the books of the Library And so
on, and so on, and so on.

One
appealing aspect of the Grand Pattern is that for any conceivable finite
assemblage of orderings in libits, infinitely many sections of the Library will
contain precisely that same distribution of books. Each new step incorporates
the preceding step as one subunit of the new step, and so each step repeats and
repeats and repeats.

Another
consequence, somewhat amusing, is that there will be abutting libits whose
distributions are, in a sense, palindromic. A librarian, fortuitously born by
the border between these two libits, would find a vast "wall" of
adjacent duplicate hexagons! Moving in one hexagon away from the border in each
direction would also reveal duplicate hexagons. Ditto for moving in two
hexagons away from the border, and so on. There are as many quirky
distributions in bordering orderings as we can imagine; after all, every
distribution appears next to every other. Could a human librarian born in such
a border locale guess that the Library contained volumes consisting of all
possible variations of 25 letters?

A sharp-eyed
reader may have noticed that we've consistently written "the Grand
Pattern," as opposed to "a Grand Pattern." This is because once
we have settled on a libit shape,
there is only one such Grand Pattern.
(See
the Math Aftermath for more about why we must choose a libit shape.) Here is
one way of seeing this mild form of uniqueness of the Grand Pattern:

Assume we've
already constructed an infinite Library with books distributed in a Grand
Pattern. Also assume, for the sake of argument, that a godlike entity also
constructs an infinite Library, and for reasons that range from the puckish to
the profound, wishes to distribute books in a
different
Grand Pattern.
This Other Entity chooses the same-shaped libit, and after envisioning a tiling
of the second Library, starts at an arbitrary hexagon, and for the first step,
distributes 25
^1,312,000
books in an allocation varying from ours.
Next, for Step 2, the Other Entity distributes books into the remaining

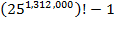
libits in a distribution
unlike our second step. And so on.

Let us add
omniscience to our list of godlike attributes. Consequently, we
know
exactly how the Other Entity will distribute the books for the first step, the
second step, etc. etc. Since every finite pattern, no matter how large, appears
in our Grand Pattern, we simply choose an initial libit from our pattern which
has the same distribution of books as the Other Entity's first step. By dint of
omniscience, in fact, we chose that initial libit so that, moving outwards, it
exactly shadows the Other Entity's second step, too. In fact, for any positive
integer
n
, we chose so well, that moving outwards shows precisely the
same distribution as the Other Entity's
n
th step; and remember, as
implausible as this may seem, we must remind ourselves that all finite
patterns, no matter how large, appear in a Grand Pattern. Finally, we observe
that since our Grand Pattern exactly mimics the Other Entity's Grand Pattern
for every positive integer
n
, it shadows it for all
n
; therefore,
the two Grand Patterns must be the same. (See the Math Aftermath for more about
this leap of logic from the finite to the infinite.)

A librarian
granted eternal life and a Funes-like infinite capacity for photographic
memories, walking a Grand Tour of the Library, reading and distinguishing every
book, would discover that no pattern reliably repeats. On the other hand, a
librarian of genius, equally endowed with the unimaginable ability to process
titanic amounts of information, might well guess that, for a choice of the
shape of a libit, the books are distributed throughout the Library in all
possible orderings. And all possible orderings of all possible orderings. And
all possible orderings of all possible orderings of all possible orderings...

As such, the books of this
infinite Library are maximally disordered; and yet this ultimate disorder forms
a unique overarching Order of all orderings: the Grand Pattern.

Math
Aftermath: Libits, Uniqueness, and Jumping from the Finite to the Infinite

It is hard to be finite
upon an infinite subject, and all subjects are infinite.

—Herman
Melville,
The Piazza Tales and Other Prose Pieces

In what follows, we briefly
discuss two subtle points from above. First, we examine why the libits must be
the same shape while comparing their respective Grand Patterns. If they are
allowed to be dissimilar, we'll use, as an example, the two extreme examples
from earlier in the chapter: we'll say a
tower libit
is a slender tower
of stacked single hexagons, while a
floor libit
is completely contained
in one floor. Imagine seven tower libits, six of them adjacent to a central
one, that are exactly the same save that in their top hexagons, four books are
permuted into slightly different positions. Then the towers are all identical
except in the top hexagons, and even there, each top hexagon contains the same
books as the others. (See figure 64.)

We claim
that no floor libit can accommodate this distribution, for any floor libit that
contains any hexagon of the central tower libit necessarily also contains a
hexagon of at least one of the adjacent tower libits. By construction, these
two hexagons must contain precisely the same books. However, no libit can have
duplicate books; thus it follows that a Grand Pattern constructed out of tower
libits cannot be replicated by floor libits. (See figure 65.)

In this part of the Math
Aftermath, we consider the leap from the finite agreement at "each
n
"
to the infinite agreement at "every
n
" that arose in the
comparison of our Grand Pattern and the Other Entity's Grand Pattern. Here is a
sequence ofideas that may help act as a bridge across the unimaginable abyss
between the finite and the infinite: suppose our Grand Pattern differed from
the Other Entity's. Then, by the well-ordering principle (see below), there is
a smallest positive integer—for example, 412—such that our Grand Pattern
differs from the Other Entity's Grand Pattern at Step 412. However, we know
that the Grand Patterns are exactly the same at each finite step, including
step 412. Thus, there can be no smallest integer at which they differ.
Therefore, they are everywhere the same!

The
well-ordering principle
is an axiom of set theory (in some less commonly used logical models of
arithmetic, it is a provable theorem). It says, in essence, that any set of positive
integers has a smallest member. Although this sounds relatively innocuous, the
constructivist school of mathematicians raises nontrivial objections to the
well-ordering principle and the theorems which spring from it. It is worth
mentioning that although these objections can never be formally refuted, there
are few working pure mathematicians who are constructivists. On the other hand,
a number of prominent computer scientists and applied mathematicians are in
sympathy with the philosophic beliefs of the constructivists; for example, for
them, a number doesn't exist unless it can be constructed. A strict
constructivist won't admit the actual existence of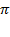
 or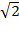
 in the sense of an endless decimal expansion; rather, such a
thinker would only acknowledge rational approximations to these irrational
numbers.