Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5 (86 page)
Read Teaching the Common Core Math Standards With Hands-On Activities, Grades 3-5 Online
Authors: Judith A. Muschla,Gary Robert Muschla,Erin Muschla-Berry
Tags: #Education, #Teaching Methods & Materials, #Mathematics, #General

Preparation
Set up three work stations. Each station should have five desks. (You can use long tables instead of desks, but you should then divide each table into five sections.) Place 20 1-centimeter cubes on each of the five desks at one station. Place 20 1-inch cubes on each of the five desks at the second station. Place 20-inch dice on each of the five desks at the third station. This setup will easily accommodate a class of 30 students. (For smaller classes you may set up fewer work stations.) To make it easy for your students to find the proper station, label each station with a number and the type of cubes it contains, for example: “Station 1: 1-centimeter cubes.”
Procedure
1.
Explain that volume refers to the space inside a container and that it is always measured in cubic units. For this activity, students will find the volume of rectangular prisms using three different-sized cubes.
2.
Explain that three work stations are set up around the room. Each station has five desks. At one station, the desks contain centimeter cubes. At the second station, the desks contain inch cubes, and at the third station the desks contain dice, which are improvised units. The order of working at the stations does not matter, but students must work at all three stations. They will work at each station for about 10 minutes.
3.
Explain that when they are at a station, they should work as pairs or in their groups and use the cubes to construct as many rectangular prisms as they can in the time allotted. Note that different pairs or groups of students may use different numbers of cubes to construct prisms with different dimensions. After students have completed a prism, they are to find the volume by multiplying the number of cubes by the volume of 1 cube. They are to record the dimensions and volume of each prism they construct.
4.
After about 10 minutes, announce that students should move to a different station. They are to follow the same procedure with a different set of cubes. After another 10 minutes, students are to go on to the third station and follow the same procedure.
Closure
Discuss students' results. Ask for volunteers to provide the dimensions, number of cubes, and volumes of some of the prisms they constructed. Instruct them to write an exit ticket explaining how the volume of a rectangular prism relates to the number of cubes and the dimensions of the cubes.
Measurement and Data: 5.MD.5
“Geometric measurement: understand concepts of volume and relate volume to multiplication and to addition.”
5. “Relate volume to the operations of multiplication and addition and solve real-world and mathematical problems involving volume.
a.
“Find the volume of a right rectangular prism with whole-number side lengths by packing it with unit cubes, and show that the volume is the same as would be found by multiplying the edge lengths, equivalently by multiplying the height by the area of the base. Represent threefold whole-number products as volumes, e.g., to represent the associative property of multiplication.
b.
“Apply the formulasand
for rectangular prisms to find volumes of right rectangular prisms with whole-number edge lengths in the context of solving real-world and mathematical problems.
c.
“Recognize volume as additive. Find the volumes of solid figures composed of two non-overlapping right rectangular prisms by adding the volumes of the non-overlapping parts, applying this technique to solve real-world problems.”
Background
Although the volume of a rectangular prism can be found by counting the number of cubes that it contains, a far more practical way to find volume is to use one of the following formulas: where
where stands for the length of the base,
stands for the length of the base,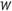 stands for the width of the base, and
stands for the width of the base, and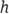 stands for the height of the prism; or
stands for the height of the prism; or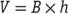 , where
, where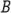 stands for the area of the base and
stands for the area of the base and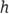 stands for the height. Because
stands for the height. Because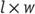 is equal to the area of the base, the two volume formulas are equivalent. Regardless of the orientation of the prism, the volume is always the same.
is equal to the area of the base, the two volume formulas are equivalent. Regardless of the orientation of the prism, the volume is always the same.
