Simply Complexity (26 page)
Authors: Neil Johnson

Wars are fought by collections of people who organize themselves into groups – for example, units, factions, brigades and armies. Decisions are then made by individuals and groups, and these decisions lead to actions and events which propagate the war itself. Most importantly, these decisions are in turn affected by past and present events – in other words, there is feedback. As a result of this feedback, the objects in question then interact in a potentially complicated way. The net result is a complex history of attacks and clashes during the lifetime of a given war, with each such attack or clash generally producing injuries and fatalities. Although of course shocking, the important point from the perspective of Complex Systems is that such casualty data can therefore be used as a measure of ongoing activity in the war.
Very recently, Mike Spagat of the University of London, together with Jorge Restrepo and his team at CERAC in Bogota, Colombia, carried out a detailed analysis of the attack and casualty data in a number of ongoing wars, including Iraq and Colombia. To their surprise, they uncovered patterns in this casualty data. Even more remarkably, they found that the patterns for the two seemingly unrelated wars in Iraq and Colombia, are currently the same. This suggests that – regardless of the origins of these two separate wars or the ideologies behind them – the insurgent groups in each war are now effectively the same in terms of how they operate.
Mike and Jorge’s research team have also managed to develop a mathematical model based on group-formation, which describes a likely scenario for how the insurgent groups are operating. The model gives very good agreement with the observed patterns in Iraq and Colombia. This good agreement implies that the mechanism described in the model has managed to capture how the real insurgent forces are currently operating in these countries. In particular, the model suggests that the insurgencies in both wars
involve a loosely connected soup of so-called “attack units” which are continually combining and breaking up over time. When a given attack unit undertakes an attack, it will tend to create a number of casualties proportional to that attack unit’s strength. Hence the distribution of strengths of these attack units should reflect the distribution of casualties which arise in the war. And this is exactly what they have found – indeed, the model reproduces almost perfectly the patterns which they have uncovered from the casualty data. Mike and Jorge’s findings are so remarkable that we will discuss them in detail in Section 9.3. But first we will go back to the early part of the twentieth century to understand the significance of such patterns.
Our story starts with Lewis Fry Richardson who worked as an ambulance driver in World War I. Richardson collected together the total casualty figures from each war that took place between 1820 and 1945 – and when he plotted them on a graph he discovered something which is quite amazing. But before I can tell you what he found we need to think about what graphs usually look like. 164
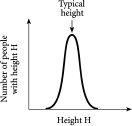
Figure 9.1
What it means to be “Normal”. A graph showing the distribution of heights of people. The number of people at a given height H is shown, for all possible heights H. Since no one can possibly be ten feet tall, and no one is less than one foot tall, it makes sense that the shape will look peaked at intermediate values and then fall off to zero on either side. Such a curve is called a bell-curve or “Normal” distribution.
Suppose we know the heights of everyone in our street, or city, or country – or even the world. If we then make a graph of the distribution of these heights we will get something like
figure 9.1
. Since no one is ten feet tall, and no one is less than one foot tall, it makes sense that the curve will rise up and then drop back down again. This also means that there will be a peak – like the top of a mountain is a peak. This peak occurs at the height which describes the largest number of people – in other words, it represents the typical height. Everyone has a height close to this value. The important point for our story is that there exists such a thing as a typical height. So imagine that we subsequently had to guess someone’s height without ever having seen them. If the peak of the curve in
figure 9.1
occurs at 5 feet 10 inches, and the spread around this value is eight inches, then we would be pretty safe in suggesting that this unknown person’s height is 5 feet 10 inches give or take about eight inches.
Many other curves would also look like this one – for example, the speed of cars on a road. In fact, in both cases the shape is this same bell-shape, or so-called “Normal” distribution. And there is a reason why: the average in each case is dictated by something structural and pre-determined, while the spread in values around the average is due to environmental
ad hoc
reasons. As far as the heights go, a person’s body has an implicit reason based on genes and inheritance to grow to a certain height. Then, if the person has an extreme oversupply or undersupply of nutrition, they will probably end up somewhere just above or below this value. The same idea holds for traffic: there is some pre-existing speed limit on a given road which tends to control the average speed of the cars; on top of that, there are everyday environmental and behavioral reasons why individual drivers may drive slightly above or below this value.
Richardson might have expected that, in a similar way, there would be a “typical” size of a war, with a typical number of casualties and a spread around this according to particular circumstances. But this is not what he found at all. Instead he found that the number of wars with a given total number of casualties
N
, decreased as
N
got bigger. In other words, the curve did not have a peak as in
figure 9.1
. The number of wars with very few
casualties turned out to be the largest part of the curve, and then the curve just decreased. Maybe this isn’t so shocking – but what he found next certainly was. Instead of just decreasing in any old fashion, he found that when he drew the graph in a certain way, the shape was essentially a straight line. In particular, when he took the so-called logarithm of the number of wars with a total of
N
casualties and plotted it against the logarithm of the number of casualties
N,
he got a near-perfect straight line as sketched in
figure 9.2
. (A “logarithm” is what you see on a calculator as “log” or “ln”. Richardson of course didn’t have a calculator – instead he had to use those old log-tables that they used to hand out in school).
This finding is quite remarkable. It is hard to think of anything less ordered or regular than war. Wars have different causes, are fought by different people in different parts of the globe, and seem so horrifyingly unique that it would appear impossible that any significant similarities would arise. Yet what Richardson found is not just a statement of similarity in words – it is a precise mathematical relationship. Going further, it is a law – a mathematical law of war. My grandfather told me of the horrors that he lived through in the trenches in France in World War I, and would have
been the first to say that there is no law whatsoever in war. But that would be wrong. World War I is one of the points on that straight line, and so are all the other wars from that era of history.

Figure 9.2
Wars are not “Normal”. Instead, the distribution is a so-called power-law. The term “power-law” has nothing to do with physical strength. Instead it describes the fact that when plotted on a log-log scale as shown schematically here, the number of wars with a total of
N
casualities against the number of casualties
N
is a straight line. Equivalently, the logarithm of the number of wars with a total of
N
casualties plotted against the logarithm of the number of casualties
N
, is a straight line.
But why would such a law of war exist? Richardson didn’t really know – but fortunately we can now explain his remarkable finding using Complexity Science. The clue lies in the so-called
universal pattern of Life
which we discussed in
chapter 3
. There we found that Complex Systems live between disorder and order, and tend to produce particular types of fractal patterns that look like
t
a
. The same holds here in that the number of wars with a total of
N
casualties follows a mathematical relationship like
N
-α
. This mathematical relationship is more generally referred to as a power-law, and α is just a number in the same way that
a
is just a number. Now imagine we grab a calculator and work out the logarithm of the number of wars with a total of
N
casualties, and plot it on a graph versus the logarithm of the number of casualties
N
. It will look like
figure 9.2
. The reason is simple: the logarithm of the number of wars with a total of
N
casualties is equal to the logarithm of
N
-α
. But the logarithm of
N
raised to the power -α is just -α multiplied by the logarithm of
N
, which is -α log
N
. That is the way logarithms work. So this means that the logarithm of the number of wars with a total of
N
casualties, plotted against the logarithm of the number of casualties
N
(i.e. log
N
) is just a straight line with a slope equal to -α. In fact, Mark Newman of the University of Michigan has recently shown that Richardson’s straight line – in which each point corresponds to the total number of casualties in a given war – has a value of α of around 1.8.
The fact that wars follow a power-law has some important consequences as compared to the bell-curve distributions typified by
figure 9.1
. First the good news. The most frequent size for a war will be one with fewest casualties, unlike the case of people’s heights. Now the bad news. Very deadly wars and attacks with many casualties will occur – rarely, but they will occur. This is unlike the case of heights, where the chances are zero that someone will be taller than ten feet. For this reason, planning for wars is inherently a complex task. House designers can happily put the height of an entrance at something less than ten feet knowing that
such a tall house-buyer will never appear. They can also put step heights above one inch, knowing that such a small person will never appear. However, the presence of a power-law means that this type of assumption will not work for wars. Unlike the bell-curve, the distribution of wars predicts that future conflicts can have an extremely wide range of casualties. This would suggest that instead of planning for the typical future war, planners should indeed plan for the worst case.
The significance of all this for our story of Complexity is as follows. We have said that a Complex System is a collection of objects interacting in some potentially complicated way in the presence of some kind of feedback. But this is also exactly what wars are. We have also made a big point throughout this book of saying that human systems involving a collection of decision-making objects, which are competing for some kind of limited resource as in the bar attendance problem, the traffic, and the market, are all excellent examples of a Complex System. But this is again exactly what we also said about a war. Whether that limited resource is land or power doesn’t matter. When it comes down to it wars are “just another” collective human activity. There is no “invisible hand” or central controller to decide who wins. Hence there is no typical war with a typical number of casualties. Instead the system of adversaries just fight it out and the whole thing takes on a life of its own – just like every other Complex System on the planet.
Aaron Clauset and Maxwell Young of the University of New Mexico recently took another look at the work of Richardson – but this time in the context of terrorism. In fact they repeated what Richardson did but used instead the number of casualties per terrorist attack rather than the number per war. What they found was equally remarkable to Richardson’s original results. Despite the fact that terrorist attacks are typically well spread out in time and in space – in other words, they occur quite rarely and are spread out all over the planet – they found that when they plotted
the logarithm of the number of attacks with a total of
N
casualties versus the logarithm of the number of casualties
N,
exactly as Richardson had done, they
also
saw evidence of a power law. In other words, the number of terrorist attacks with a total of
N
casualties varies according to
N
-α
. When they restricted themselves to terrorist attacks occurring in (what were then) non-G7 countries, they found the value of a to be 2.5. For terrorist attacks occurring in G7 countries, they also found a power-law, but with a now equal to 1.7.
