Simply Complexity (23 page)

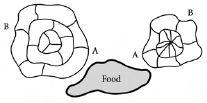
Figure 7.4
We may look different, but we act the same. As a result of congestion at busy hubs, the two structurally different networks shown above have the same functional properties. In particular, food takes the same time to cross from A to B in each structure. Moreover, both structures are optimal in that this time is a minimum for each structure.

So what happens when we put together the hub-and-spoke road network with the decision-making models discussed earlier in this book? In the setting of a corporate structure such as
figure 7.2
, we might ask ourselves whether we should try to access higher levels of a large organization in order to get a message through from A to B. More generally, should we climb the corporate ladder or is it better to stick to the level we are already at? The big problem is overcrowding. If everybody tries to access higher levels of an organization, or equivalently access the hub or center of a transport network, it will become increasingly congested. In terms of a message, it would be better to transmit it within our own level as far as possible. However the rate of transmission through our own level may be very slow if it includes lots of people. So this is another of our “choose option 1 or option 0” type problems – in other words, traffic dilemma No. 3 in the list given at the beginning of this chapter.

Sean Gourley has looked at the problem of decisions on such hub-and-spoke networks in detail. He allowed the cost of using the central hub to be a variable cost that is dependent both on the number of agents using the hub and the capacity of the hub. In particular, the central hub has a comfort limit given by
L
, as in
chapter 4
for the bar. If this limit is exceeded, then the hub becomes congested and a congestion charge is imposed on the subsequent traffic through the hub. Each agent must repeatedly decide whether to go through the central hub or around the outside – exactly as in
chapter 4
when deciding to attend the potentially crowded bar or not. Sean found that the resulting traffic patterns are very rich in their behavior. This richness arises from the interplay between the creation of, and the transition between, particular stable traffic states which arise as the conditions on the network change. His results show that the existence of congestion in the network is a dynamic process which is as much dependent on the agents’ decisions as it is on the structure of the network itself.
Figure 7.5
summarizes his results, showing that there is an optimal number of connecting roads that should be made available – for most possible values of the congestion charge – such
that each driver spends a minimum amount of time and money getting from one side of the network to the other. This result is therefore consistent with Tim and Doug’s findings. In addition to biological systems, Sean’s results lend themselves to the many real-world situations discussed earlier – communication across social/business networks, flow of data across the Internet, air traffic, and any other situation in which competing, decision-taking agents have to navigate across a network in which congestion might be a factor.

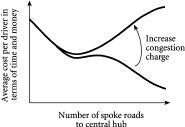
Figure 7.5
Should all roads lead to Rome? Sean Gourley’s research results show the effect that additional spoke roads will have on the average cost per driver in terms of time and money.

So let’s just take a moment to summarize where we are with traffic, and where traffic research is heading in relation to Complexity Science. Traffic is an interesting example of an interacting multi-particle system (i.e. cars) on a non-trivial topological network (i.e. roads). Many traffic studies have taken the view that cars follow automata-like rules. This is probably a good approximation for dealing with traffic which is already
on
a particular road; however, it does not address the arguably more fundamental question of why those cars, or rather their drivers, chose that route in the first place. For that, we need the multi-agent decision-making models of Complexity Science as discussed above and as highlighted in
chapters 1
and
4
. Indeed with in-car access to real-time traffic information already available and likely to become more prevalent in the future, an understanding of how motorists’ individual decisions feed back onto the emerging traffic pattern and vice versa, is of great practical importance for all of us.

“I’ve found the perfect person” is a cry you don’t hear very often. Why? Because the task of finding Mr./Ms. Right is complicated. Indeed it is so complicated that many people never seem to manage – or think they have managed only to decide later that they have made a mistake.

As many of us might already know to our cost, there are several reasons why finding Mr./Ms. Right is so complicated. First, in order to find that truly perfect person, that person must actually exist. Even if we assume that such a person could in principle exist at some stage in the evolution of mankind, there is no guarantee that they haven’t already lived and died before we were born – or will be born after we are dead and buried. Hence it might happen that even if you could trawl the entire planet, you would still never find your perfect match. Worse still, the partner who we didn’t think was perfect at some stage in our distant past, may at some later stage seem perfect – but the opportunity has already gone. Second, you actually have to establish contact with this perfect person. The fact that Mr./Ms. Right might live five blocks from you but you never come across them, is a particularly unfortunate but possible event. And just as there are different blocks to explore, there are different towns, countries – and even continents. Third, even if you find your perfect match, you may not be
the perfect match for them. Whole sections of literature, comedy and real-life drama, are built around such situations of romantic frustration. Indeed this frustration is reminiscent of the three-file frustration we saw in
chapter 2
: person A loves person B who loves person C who loves person D who loves person A. Tragic, but true – and very complex.

So those are three major obstacles getting in the way of our search – and here is a fourth, which is also potentially the most complicated: you are not the only one looking. That again sounds obvious, but the fact that you and everyone else is simultaneously looking for that special someone means that we are once again faced with a scenario where we are competing with everyone else for something. In particular, we are each part of a collection of decision-making objects competing for a limited resource, which in this case is the perfect partner. For this reason, looking for a date is as good an example of Complexity as the bar attendance problem, the commute to work, or choosing stocks in a financial market. They are all Complex Systems – hence our interest in spending a chapter looking at this particular problem of pairing.

We spend an enormous amount of time and effort in our lives forming and maintaining relationships of all sorts – including dating and finding friends. Indeed, building relationships is a fundamental human activity. Commercial and political relationships are also fundamental to our Society. For example, as consumers we are all individually in customer-client relationships with particular gas, electricity and phone companies; our employers are typically involved in business partnerships with other companies; and our countries are involved in ever-changing political, strategic and commercial alliances (e.g. the EU and NATO). And, as they say, even “birds and bees do it”. Indeed, Nature is awash with various types of mating and grouping rituals. In short, the fact that we are not alone on the planet makes the dynamics of relationships the driving force behind our Social Life on Earth.

But if everyone and everything does it, why does it sometimes seem that we aren’t very good at it? Moreover, as people become more sophisticated – or just downright picky – in their requirements for a partner to date, does this mean that Society as a whole is going to be driven to a state where most people are not in a
relationship? We are often told that Society is breaking up because we are getting too choosy and hence too ready to break off existing relationships – but is this really so? Similar questions can also be asked of our commercial allegiances to particular products, brands, companies or loyalty schemes – such as airline frequent flyer programs.

The key conundrum for many people is whether to hold out for the perfect partner, Mr./Ms. Right, or just make do with Mr./Ms. Right-Now? Richard Ecob and David Smith set about attacking such relationship questions from the perspective of a Complex System – in other words, they have used mathematics and computer simulations to look at how collections of us behave when we wander around within our own social networks looking for the right partner. In addition to helping understand human dating, their results can be applied to situations involving animal mating, businesses seeking out customers, consumers finding a website for their particular needs on the Internet – and even antibodies tracking down viruses. In technical jargon, this problem is very close to the interests of physicists in the areas of reaction-diffusion of particles on networks, and the complex dynamics of far-from-equilibrium systems.

So what exactly did they do and what can they tell us? Their approach was to combine computer modelling with mathematical analysis – and it turns out that their mathematical analysis exploits a remarkable and unexpected connection with the phenomenon of radioactive reactions in nuclear physics.

Their computer model featured an artificial society where relationships could form between “software singles”, thereby simulating the scenario of people searching for partners. A spatial network was introduced to represent the social network within which the agents could move and interact. They started the simulations off with roughly equal numbers of men and women. Each person was allocated a list of “personal preferences” which they could use to assess the compatibility of potential partners
whom they came across on their travels around their social network. For example, suppose the hub-and-spoke network of
chapter 7
were to be chosen as an appropriate social network – this would be suitable for people who have one major meeting place (e.g. work) and then occasionally visit a range of others (e.g. cinema, gym, supermarket). These software people then wander around from site to site, each carrying their own personal list of preferences. These preferences define the person’s likes and dislikes – in particular, the list of preferences such as “likes jazz, doesn’t like classical music, likes spicy food, doesn’t like museums, likes dancing” can be thought of as a person’s phenotype, which is a word borrowed from the language of genetics. However, in contrast to the situation in genetics, these preferences are not assumed to be innate – instead they may change in time or arise purely as a result of the person’s personal circumstances (e.g. income, lifestyle).

The number of agents per phenotype, the density of agents per social site (e.g. the gym), and the connectivity of these sites, are key quantities in terms of dictating what happens to the population as a whole. Varying these numbers has the potential to change quite significantly the outcome of the computer model and hence the prediction of what happens in real life.

So let’s look at the dating arrangements which their computer model used. Suppose some of the males and females meet at a particular social site at a particular time. They then go ahead and compare their personal preference lists – i.e. phenotypes – to see how well-matched they are. If this matching is sufficiently high, they can start a relationship. This pair then stays together an amount of time which depends on how similar the two lists are. In other words, they stay together a longer time if their tastes and interests are similar, and hence if their phenotypes are similar. The model can be easily generalized – for example, the researchers are able to explore the effect of making the people in the relationship gradually change their lists over time so that there is the potential for couples to naturally “drift apart”.