Simply Complexity (11 page)

Figure 3.3
Not too ordered, not too disordered, but just right. Most of the shapes which we observe in the real world, are neither too smooth (i.e. too ordered) nor too jagged (i.e. too disordered). In technical jargon, they are referred to as fractals.

Real mountain ranges and coastlines look to be better described by a value of
a
between 1 and 0.5, and hence a fractional dimension
D
between 1 and 2. In other words, mountain ranges and coastlines seem to be fractal. And here is the interesting piece of news – so does nearly everything else. More precisely, it does seem to be at least approximately true for a large number of complicated patterns which emerge in our everyday world. In later chapters we will mention specific examples in the economic and sociological domains. But for now, we will just try thinking through the consequences of having such a seemingly “universal” pattern in our lives. The fact that the value of the parameter
a
lies between 1 and 0.5, and hence the fractional dimension
D
lies between 1 and 2, means that the output time-series lies somewhere in the murky region between complete order (
a
= 1) and complete disorder (
a
= 0.5). But why should so many other things in our lives also inhabit this murky region?

To answer this, let’s think for a moment about music. When many people who are not musicians sit down at a piano, they try to play something simple like
Three Blind Mice
. However, I bet there are not many people who have chosen to download
Three Blind Mice
onto their MP3 player. Why? Because it is a boring tune. In fact if you look at the shape of the music for
Three Blind Mice
, as sketched in
figure 3.4
, you can see that it is very ordered – too ordered to be interesting, in fact. Now, when we hear a piece of music played on a piano, for example, the shape becomes the
output time-series of the piano – in other words, music can be seen as the output time-series from a system comprising the player and the instrument. Hence an equivalent way of explaining why simple tunes like
Three Blind Mice
seem boring is that the output time-series is too ordered.

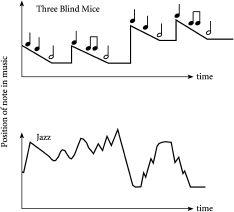
Figure 3.4
The shape of music when written out on music paper, or equivalently when played in time on an instrument. Top diagram shows a very ordered and hence boring piece such as “Three Blind Mice”. Bottom shows a less ordered and hence more interesting piece, such as part of a jazz solo in bebop style.

By contrast, the music that many people would class as interesting – including classical music by composers such as Bach through to modern jazz – has a far more complicated structure. In other words, it is far less ordered, or equivalently far more “surprising”. Indeed such music typically has, when viewed on a page as in
figure 3.4
, a fractal-like shape containing patterns within patterns. In particular, the bottom diagram in
figure 3.4
shows the pattern of one of the saxophone solos of Charlie Parker, who was one of the legends of Bebop and hence modern jazz. It is a much more intricate pattern than
Three Blind Mice
, and contains “patterns within patterns” as we had for the fractal shapes with
a
between 0.5 and 1. It turns out, however, that if the shape of such
music gets too disordered – in other words, the value of
a
gets too close to 0.5 and hence the shape looks too jagged – it begins to sound too much like a random arrangement of notes as opposed to interesting music. And this is precisely the point: the music we find interesting is neither too ordered – for example, like the simple patterns in
Three Blind Mice
– nor too disordered, such as we would get with a random-walk of notes moving up or down according to the flip of a coin. Exactly where we would each draw the line is a matter of taste, or dare I say sophistication. But the fact is that we all like our music to be not too ordered and not too disordered. Indeed, maybe we should actually classify our tastes by our preferred “
a
” value, or equivalently the corresponding fractal dimension
D
. It certainly might make choosing CDs for someone’s birthday that bit easier.

In addition to the melody itself, fractals in music can arise due to the set of chord extensions used – such as a minor 6th – and also from the chord sequences and associated percussive rhythms. So even if the melody of some music might appear relatively simple, as long as the chord structure or rhythm section are sufficiently fractal then the end result can be just as interesting.

I just want to briefly come back to modern jazz before moving on to the major point of this section. Modern jazz is not to everybody’s taste. But of all the different styles of music, I would argue that modern jazz is the closest to a true Complex System and hence closest to the musical equivalent of Complexity. Thinking back to the key components discussed in
chapter 1
, this makes sense. Modern jazz involves a spontaneous interaction of a collection of objects (i.e. musicians). It exhibits surprising emergent phenomena in that it is improvised, and hence what emerges in a given solo is a product of the actual feedback which that soloist receives at that moment in time. It is also an open system in that its best performances arise in an environment with audience feedback. It even has the feature of extreme behavior when, for example, the whole ensemble begins to mimic the pattern being played by a particular soloist, and hence there is a crowd effect in which the whole group begins to synchronize its phrasing. Above all, it has no “invisible hand” such as an orchestral conductor or an existing piece of melody that all the players are simply repeating.
Instead solos are built on the patterns, motifs or “licks” that a given player has in his memory, and which are then interwoven with original ideas in a truly complex way – all set against a loose backdrop of chord sequences. Just take a listen to the Brecker Brothers album
Heavy Metal Bebop
, in particular the track
Some Skunk Funk
. To me it embodies everything that Complexity is – and if you ever happen to see a transcription of Michael Brecker’s tenor saxophone solos for that record, you will see fractals dancing before your eyes. If, however, you prefer something a little bit easier on the ear and more popular, listen to the patterns being woven in the alto saxophone solo played by Phil Woods on Billy Joel’s
Just The Way You Are
.

The fact that we like fractal music is very interesting in itself, since it turns out that many things around us in Nature are also fractals in either space or time. Even our own heartbeat which is supposed to be so regular, is actually a fractal. Indeed the healthier your heart is, the more fractal it is since the added Complexity – over and above what would correspond to a strictly clockwork heart – allows the body to adapt to a wider range of possible situations. So our heart is a Complex System which produces a fractal output time-series – in other words, a fractal in time – and the fact that it lies between complete order and disorder gives it adaptive power. In fact, the notion that there are benefits to sitting on the edge between order and disorder, and hence having adaptive power, rings true in our everyday lives. As we all know, a workable daily schedule cannot be made too rigid or ordered since any small blip would then make the whole thing collapse. Instead, a certain level of flexibility is very important if we are to adapt to unexpected events. Our hearts follow the same tactic – and so does the music we find most interesting.

As hinted at earlier, there are also many everyday examples of fractals which appear as patterns in space as opposed to patterns in time. For example, the skyline of many cities and the typical shape of many mountain ranges are essentially fractals in space. Indeed the reason why so many spatial fractals appear can again be understood in terms of Nature and Society working in such a way that the resulting forms are neither too ordered nor too disordered. In mountain ranges, it is likely that whatever physical
process caused the roughness of a particular mountain, also gave rise to a similar roughness on a nearby peak. Hence there is a persistence in the amount of order as we move from peak to peak, exactly as we needed for our walker in order to produce a fractal with a value of
a
between 0.5 and 1. Such persistence can also be referred to as a correlation in the behavior of neighboring parts of the same mountain range, just as the persistence in an output time-series can be referred to as a correlation in the output from one moment to another. In this language, what stops the melody of
Three Blind Mice
from being interesting is that it is just too correlated. A similar argument holds for the skyline of cities. It is likely that the height or shape of a given building would somehow have been chosen to fit in with those nearby – at least if the city planners have done their job. And since we seem to find fractals so aesthetically pleasing, judging from our tastes in music, it is little surprise that a pleasing city skyline will also correspond to such a fractal. Even art is a form of fractal, and the art that we tend to find most interesting is also in that middle-ground between complete order and complete disorder – in other words, between being completely boring and completely unintelligible.

So fractal shapes are a fairly ubiquitous feature of Complex Systems. In other words, they represent a fairly common emergent phenomenon from Complex Systems, in which the system behaves in time as though it is bouncing around in the middle-ground between complete order and disorder. In the same way, the shapes that a Complex System exhibits in space also appear to live in this middle-ground. However, fractals are not the only things that can arise in a Complex System. As we saw earlier, periodic behavior can also occur – so can purely static behavior. What makes a Complex System truly complex is the way in which it gives rise to such effects
and
how it manages to move between such different types of behavior. So while it is sometimes stated in the popular press that our lives are “on the edge of Chaos” and that everything in our world can be explained using fractals, such claims represent a gross over-generalization.

In the rest of the book, we will focus on real-world Complex Systems rather than the toy versions that we have discussed in this chapter. But before we do, it is worth thinking about how we actually observe a Complex System. After all, this is a very important issue given the standard approach of scientific research, which is to observe something, then measure it, then develop a model or theory, and then test this against the observations. Indeed if we are not observing the system properly, or if the way in which we are observing the system is unintentionally biasing our measurements and hence deductions, we will be in trouble.

The natural assumption to make is that the act of observing a Complex System does not in itself affect our interpretation of what we think is going on. But this can be misleading. Just think of the following two extreme examples. Suppose we want to investigate whether there is any pattern in the arrival times of trains at a particular station. Let’s suppose that the whole rail system always runs perfectly on time but that we unwittingly turn up at a different time each day and do not know the precise time. Based on our observations, we would probably end up wrongly concluding that the trains themselves arrive at random times. As a second example, imagine something that is observed regularly and in the moment of being observed always has the same form. For example, imagine a child who is always in bed asleep between 8 p.m. and 6 a.m., and yet spends his days running around in an essentially random way. A visitor from another galaxy who only visited between the hours of 8 p.m. and 6 a.m., and who knew nothing about human life, might wrongly conclude that humans spent their lives in a very ordered fashion, asleep in bed. The moral of these two stories is that we have to be careful how we are watching. We must be careful not to add any Complexity which isn’t already there, nor must we miss the Complexity which is actually there. This is an important practical point for Complexity Science as a whole, and has particular relevance for some of the applications discussed later in this book.

The things that we observe around us – such as traffic, financial markets, and even ourselves – tend to occupy the middle-ground between order and disorder, making occasional forays toward one or the other and back again without the help of any “invisible hand” or central controller. It is the emergence of such properties that make a Complex System complex, and sum up what we mean by Complexity. The magic ingredient underlying these remarkable properties is feedback.