Pythagorus (19 page)

Aristoxenus' public relations efforts did not succeed well. Through the fourth century B.C., the popular image of Pythagoreans continued to resemble the
acusmatici
more than the
mathematici
. But after the fourth century, the
acusmatici
, with a few exceptions, dwindled and vanished from notice. Had there been no other Pythagorean tradition than theirs, and if they did indeed represent the truer image of Pythagoras and his earliest followers, it would be almost impossible to explain how such an odd cult figure, not far different from others in antiquity, became so dramatically and rapidly transformed in the minds of intelligent men and women as to inspire deep and effective scientific thinking and seize the imagination of centuries of people to come.

Was it all due to Plato? Did he get so excited about something that was mainly legend that he elaborated on it himself until he had made it hugely significant? At a minimum there had to have been the discovery in music of pattern and rationality underlying nature, and the accessibility of that rationality through numbers – and that was of no small significance. It seems much more reasonable to conclude that Pythagoras, responding to different types of interest and intelligence among his followers, encouraged both kinds of thinking –
acusmatici
for those who needed something naive and more regimented and conservative, and
mathematici
for those with minds eager to grasp difficult, nuanced concepts and explore their implications. He was personally, perhaps, not entirely unlike either group.

However that may be, from the time of Plato, what survived as ‘Pythagorean' and ‘Pythagoras' was largely
mathematici
, and that included the conviction that right from the time of Pythagoras himself, and attributable to him, there had been a truly remarkable new approach to numbers, mathematics, philosophy, and nature.

CHAPTER 9

‘The ancients, our superiors who dwelt nearer to the gods, have passed this word on to us'

Fourth Century B.C.

Socrates was not Plato's
fictional creation. Born about thirty years after the death of Pythagoras, near the time Philolaus was born, he fought in the Peloponnesian Wars and then lived a life of intentional poverty as a teacher in Athens. He wrote nothing, and information about what he taught comes only through Plato's dialogues and similar conversations recorded by Xenophon, another of Socrates' pupils. Socrates' teaching method consisted of asking questions. Plato's dialogues are not word-for-word accounts of real question-and-answer lessons, but are almost certainly faithful to the philosophy as it emerged in conversations like these. When Socrates was seventy, he was accused of impiety and corrupting the youth of Athens. A jury of his fellow citizens sentenced him to death, probably through a dose of hemlock. He died surrounded by his friends and pupils.

In the dialogues Plato wrote, the character Socrates usually directed the discussions, but in Plato's
Timaeus
he relinquished centre stage for many pages to a fictional character named Timaeus of Locri. Timaeus was supposed to be a statesman and scientist from southern Italy, and the ideas Plato put in his mouth were heavily indebted to Archytas, with whom he had apparently spent long hours in Tarentum deep in conversation and bent over mathematical diagrams. Perhaps what Timaeus tells Socrates and his friends in the dialogue is close to what Archytas laid out for Plato. Or maybe Archytas' ideas were only a springboard for Plato. Though many opinions have been expressed about those possibilities, no one knows for certain, and the truth likely lies somewhere in between.

Plato carried forward two great Pythagorean themes: (1) the underlying mathematical structure of the world and the power of mathematics for unlocking its secrets; and (2) the soul's immortality.
1
The stage is set for discussion of the first when Socrates asks Timaeus, an expert on such matters, to ‘tell the story of the universe till the creation of man'.
2
Timaeus' response to this daunting request is a number-haunted, Pythagorean creation story: The mathematical order of the universe was the work of a creative god, whom Plato called the demiurge – not the chief god or the only god, but a figure loosely comparable to Ptah, the Egyptian god at Memphis, or to Jesus acting in the role of the
logos
in the opening of the Gospel of John – ‘through him all things were created'. This craftsman god, says Timaeus, decided that the universe should be a ‘living being', spherical and moving in ‘a uniform circular motion on the same spot; unique and alone'. Timeaus sets forth a numerical construction of the ‘world soul':

• First the creator god took his material and ‘marked off a section of the whole'.
  

• Then he marked off another section ‘twice the size of the first'.
  

• Next he marked off a third section, ‘half again the size of the second section and three times the size of the first'.
  

• Next he marked off a fourth section, ‘twice the size of the second'.
  

• Next, a section ‘three times the third'.
  

• Next, a section ‘eight times the first'.
  

• Last, a section ‘twenty-seven times the first'.
  

Counting the squares in each line gives 1, 2, 3, 4, 9, 8, 27. The first four of those numbers are the numbers in the
tetractus
and the Pythagorean musical ratios, 2:1, 3:2, 4:3, but it is an interesting challenge to discern a meaningful pattern in the rest of the numbers, and how they could work in a creation scheme. The answer is that if you square each of the first two numbers 2 and 3 (1 not being a ‘number'), you get 4 and 9. Cube the same two numbers, 2 and 3, and you get 8 and 27. For a Pythagorean it was significant that each pair was an even and an odd number. Plato stopped with the cubes because in the creation of three-dimensional, solid physical reality, only three dimensions are needed.

Next, according to the account Plato put in Timaeus' mouth, the creator divided his material into smaller parts, filling in harmonic and arithmetical means between those numbers and connecting the ‘world soul' with a diatonic scale in music.
[1]
Plato used a scale developed by Philolaus, not the one developed by Archytas.

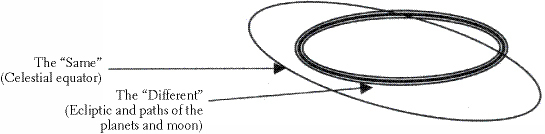
Astronomy in his
Timaeus
was also worked out in numbers, with the ‘world soul' cut into two strips bent around to form an ‘X' at one point, making an inner and outer ring. Two such rings really exist in astronomy, the celestial equator and the ecliptic. The celestial equator is on the plane of Earth's equator and anchors the sphere of the fixed stars that do not change their positions in the sky relative to one another and the celestial equator. This was the ring Timaeus called ‘the Same'. It stays the same and never changes. The ecliptic is the circular path that the Sun appears to follow in its daily round, with the planets appearing to orbit in a band centred on it. This ring was Timaeus's ‘the Different', for it changes He called the planets ‘instruments by which Time can be measured'.
[2]
The creator cut the Different into seven narrower strips to accommodate Sun, Moon, and five planets, with the radiuses of their orbits proportional to the numbers 1, 2, 3, 4, 8, 9, and 27. Both rings – Same and Different – were in constant motion, which, Plato thought, nothing but a living soul could be, unless something else pushed it. The rings moved in opposite directions, the Same east to west, the Different west to east, and the seven strips of the Different moved at different speeds, corresponding to the speeds of the Sun, the Moon and the planets.

Plato had Timaeus explain that the movement humans see in the sky is the result of this combination: The daily rotation of the Same with the sphere of fixed stars carries everything around with it, east to west, including Sun, Moon, and planets. But the Sun, Moon, and planets – the seven bodies of the Different – have in addition their own contrary west-to-east motion against that background. They ‘swim upstream', so to speak, against the current of the Same, at varying speeds, and sometimes back up. This, says Timaeus, is because they are souls, and souls exercise independent choices and power of movement. It is believed to be one of the Pythagorean triumphs, showing up in Philolaus' fragments, in more detail in Archytas' work, and then in Plato, to have explained heavenly motion correctly as a combination of opposite movements.