Pythagorus (16 page)

An anachronistic, late fifteenth-century A.D. drawing, from a music theory book by Gaffurio, reveals how scholars of that era envisioned Pythagoras (and Philolaus, who was not actually Pythagoras's contemporary) studying the ratios of musical harmony.
Though it hardly seems fair to Philolaus, anyone looking for specifics about Pythagoras and what he taught is frustrated by the fact that Philolaus was a splendid thinker in his own right. He was writing his own book, not recording the discoveries or words of another man, and included his own thinking as well as what had evolved in the Pythagorean
mathematici
communities since Pythagoras' death. Nevertheless, Philolaus definitely considered himself a Pythagorean, and, given the time frame, much of the science and doctrine in his book must have been a direct reflection of Pythagoras and his earliest followers. Philolaus was almost a direct link, for Pythagoras had died or disappeared from public view in 500 B.C., only twenty-five years before Philolaus' birth. Philolaus' teachers and acquaintances as he grew up in Croton or Tarentum must have been almost exclusively Pythagoreans, and some of the older of them would have known Pythagoras.
Unfortunately, Philolaus treated all of his material as a unified body of knowledge, making no distinctions between earlier and later, between the time Pythagoras was alive and the time of Philolaus' writing, or between himself and others. He was not being careless. For a Pythagorean there was unity to truth, and unity to the search for it. The path to knowledge about the universe and the path to reunion with the divine were one and the same path. Truth about nature, and divine truth, were one and the same truth. In such a context, even if Pythagoras himself had not made a particular discovery, one could assume it had been implicit in his teachings. Furthermore, there was a form of ancient one-upmanship that Pythagoreans like Philolaus shared with their contemporaries. It was demeaning to an idea or discovery to call it new or original. Knowledge became more credible the older it was and the more it could be attributed to a great figure. Philolaus would have been loath to identify any source other than Pythagoras, even if it was himself.
Nevertheless, Philolaus was not without an agenda of his own. One of the clues that place his writing in the late fifth century B.C. was that he was trying to present Pythagorean ideas in a way that responded to a stalemate arising from âEleatic' teaching.
The philosopher Parmenides was from Elea (hence âEleatic'), a Greek colony north of Croton on Italy's west coast. According to Plato he was born in 515 B.C., but Greek chronicles say about 540. In either case, he was a younger contemporary of Pythagoras, but remarkably, in spite of the overlap of their lifetimes, the close proximity of Elea to Croton, and a passage in Plutarch that says Parmenides âorganised his own country by the best laws', only one early source gave Parmenides even the remotest link with Pythagoras or the Pythagoreans. The link was indirect, in Diogenes Laertius' third-century-A.D. biography of Pythagoras:
[Parmenides] was also associated (as Sotion said) with Ameinias, son of Diochaites, the Pythagorean, a poor man but of good character. It was rather Ameinias that he followed: when Ameinias died he set up a shrine for him (Parmenides came from a famous, wealthy family); and he was led to calm by Ameinias and not by Zeophanes.
It would seem that if Parmenides âfollowed' Ameinias, was âled to calm' by him, and thought so highly of him as to set up a shrine, then Parmenides' own thinking would show traces of Pythagorean ideas. Lured by this clue, scholars have repeatedly attempted to find elements of Pythagoreanism in Parmenides' writing, with no success.
In a paradoxical twist, history celebrates Parmenides for insights that he did not claim were correct; for example, that the light of the Moon âalways gazing at the rays of the Sun' is reflected light.
4
He laid out such ideas in Part 2 of a beautiful, enigmatic poem, after he had warned in Part 1 â a guide to the Way of Truth â that what he was going to present in Part 2 was âdeceitful'. He was not claiming to present âfacts' or even opinions, only what human opinion on these matters might plausibly be at best.
He argued that those setting out on a voyage of âinquiry' probably mistakenly believed they had a choice between two subjects, things that existed and things that did not exist. But nonexistent things were unthinkable and unsayable, and inquiry into them was âa trail of utter ignorance'. As for what existed, certain things had to be true about it: It had always to have existed, and it had to be indestructible. Otherwise there would be a chance it might at some time not exist, which was unthinkable and unsayable. It had also to be continuous in space and time (no gaps), unchanging and unmoving, and finite. Human senses told one otherwise, admitted Parmenides, but they could not be trusted. So much for any possibility of learning about the world by observing and experiencing it!
Melissus, another âEleatic' philosopher, was an admiral from Samos, though his and Pythagoras' lives there did not overlap. As Aristotle told the story, in 441 B.C. Athens declared war on Samos. The Samians defeated Pericles himself in a sea battle, but Pericles survived and hostilities continued. When a stalemate dragged on, Pericles, bored and underestimating the Samians, led some of his ships away on an expedition. Melissus, commanding Samos' fleet, took this opportunity to attack, âdespising the small number of their ships and the inexperience of their commanders'.
5
This time the Athenian fleet suffered a devastating defeat. Samos destroyed many enemy ships, captured war supplies, and gained control of the eastern Mediterranean.
Melissus also found the time to write a prose version of Parmenides'
Way of Truth
, introducing new arguments to support Parmenides but disagreeing with him on key points. Melissus argued that whatever existed had to be infinitely extended in all directions, not be finite as Parmenides thought. For that reason, no more than one thing could be in existence. Melissus believed even more strongly than Parmenides that sense perception was an illusion, that reality was completely different from the way it appeared.
Zeno, like Parmenides, was from Elea. He came up with forty different arguments to support Melissus' assertion that only one thing could exist, produced four arguments to show that motion was impossible, and carried similar issues â including the concept of infinity â to even greater extremes, some have said to the point of intellectual nihilism. Zeno is believed to have been the author of a book called
Against the Philosophers
, which almost certainly meant âAgainst the Pythagoreans'. His criticisms may have influenced a change in their way of thinking that showed up in the work of Philolaus, about whether a point in geometry has any dimensions.
The Eleatics' penchant for a strictly abstract, logical approach and their distrust of sense perceptions was, in turn, a reaction against thinkers like Thales, Anaximander, and Anaximenes, all of whom may have taught Pythagoras. Observational evidence had seemed no illusion to them, and they suggested that substances such as water (Thales) and air (Anaximenes) were fundamental reality. Anaximander had been more abstract, but he implied a âmany' that did not gel with the concept that only one thing exists. These ideas set the stage for Philolaus. He chose not to take on the Eleatics directly, but continued to value the possibility of studying nature using the tools of the five senses.
Philolaus dealt with old questions: How did everything (the cosmos, or âworld order') begin? What basics â âfirst principles' (
archai
) â had to be in place, or had to be true, in order for anything else to happen? He answered in the first sentence of his book: âNature in the cosmos was fitted together harmoniously from unlimited things and limiting things, both the cosmos as a whole and all things within it.' The key words were âharmoniously', âunlimited', and âlimiting'.
[2]
The ideas of the âunlimited' and the âlimiting' were older than the Eleatics or the Pythagoreans, the first known mention having come from Anaximander. âHarmoniously' was uniquely Pythagorean.
If Pythagoras did study with Anaximander, he learned that for him the first principle was something more abstract than Thales' water. It was the âlimitless' (or the âunlimited') â characterless, indefinite, unbounded by time or space. The primordial description in Genesis of the earth âwithout form and void' is close to the same idea. So is the late-twentieth-century scientific concept that describes the universe (or âpre-universe') as a state of wobbling quantum nothingness from which anything (or nothing) could have emerged. The âlimitless' was a situation with no differentiation, no choices made, no orders given, no laws laid down that would allow or compel some things to happen but not others. It was the âlimiting' that was responsible for differentiation. Anaximander did not, however, think of the limitless only as a situation that preexisted the world, that came first chronologically and ended when the heavens and the world emerged. The limitless was a fundamental background to eternally continuing cycles of destruction and generation. He associated the limitless with
time
.
If Philolaus can be taken as an example, Pythagoreans also believed that the fundamental principles limitless and limiting were both needed in order for anything else to exist, which raised a problem. The two principles were discordant and opposed to one another; how could they work together to produce anything? There had to be another first principle. The limitless and the limiting âmust necessarily be locked together by a
harmony
if they are to be held together in a world'. Harmony had also to be a âfirst principle', one of the
archai
, maybe the most fundamental of all.
The word
harmonia
was not coined by Pythagoras or Philolaus. As early as Homer's
Odyssey
, it meant joining or fitting together. In carpentry it meant a wooden nail or peg. In music it referred to the stringing of a lyre with strings of different tension. The Pythagoreans gave it new importance. In the ratios of music, they felt they had found an actual link between
harmonia
on the everyday level and the
harmonia
that helped create the universe and that bound it together. They had come to think of the ratios of musical harmony as exemplifying the primordial organising principle of the universe.
The musical interval of the octave was the âfirst consonance', which Philolaus identified by the name
harmonia
. The âsecond consonance' was the interval of a fifth; the next was the interval of a fourth. Add the four numbers in these ratios (1, 2, 3, 4) and the result is 10, the perfect number.
[3]
The numbers 1, 2, 3, and 4 had additional significance for Philolaus. They underlay the progression from point to line to surface to solid:
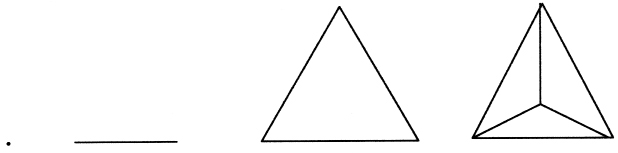
A point (on the left) is 1; a line is 2 (defined by two points, one at each end); a surface is 3 (defined by three points, one at each corner); a solid is 4 (defined by four points, one at each corner).
Later, Speusippus, Plato's nephew and successor as head of his Academy, explained what he understood Philolaus to have meant: âThe point is the first principle leading to magnitude, the line the second, the surface the third, the solid the fourth.' This sounded more complicated, but it allowed the progression to apply to other shapes and solids besides the triangle and pyramid; for example, a square, with four corners, led to a cube, with eight.
According to Philolaus, the Pythagoreans took the number 10 and ran with it. Aristotle later commented that they âconstruct the whole heavens out of numbers'. Ten being the perfect number, there had to be ten major heavenly bodies, though no one could see ten in the sky. Also, said Philolaus, there had to be fire both at the centre of the universe and at the highest point, surrounding everything, at the outermost circumference or âuppermost level'. This was partly observable, for the stars were fires out on the periphery, but what about the centre? Here, according to Philolaus, the Pythagoreans made a leap that set them far ahead of their contemporaries. The Earth could not be the centre of the cosmos, nor, for that matter, could the Sun. The centre had to be a âcentral fire', a fiery âhearth of the universe' around which the Earth, the Moon, the Sun, the five planets, and the stars revolve. As the scholar Aëtius â probably of the second century A.D. â described it, âUnlike other philosophers, who say that the Earth is at rest, Philolaus the Pythagorean said that it revolves about the fire in an inclined circle like the sun and moon.' In the centuries when no one â with the singular, brilliant exception of Aristarchus of Samos, who proposed a sun-centred cosmos in the third century B.C. â was willing to consider a moving Earth that was not the centre of the cosmos, scholar after scholar tried to show, or simply assumed, that the Pythagoreans could not really have meant this.
