Life's Ratchet: How Molecular Machines Extract Order from Chaos (29 page)

FIGURE 6.9.
Motion of a kinesin molecule (highly simplified). A: Foot 2 binds an ATP molecule, while foot 1 degrades ATP (T) to ADP (D) and detaches from the track. B: Binding ATP (T) causes foot 2 to clamp on tightly to the microtubule track and allosterically bend its leg forward. Meanwhile, foot 1 has released from the track (arrow a in step A) and dangles back and forth (arrow c). C: But because foot 2 and its leg have tilted the molecule forward, forward motion is favored for foot 1, and eventually it will weakly bind to the track in front of foot 2, releasing ADP, as seen in arrow d. The molecule has taken a step. Finally (not shown), foot 1 binds an ATP, clamps on tightly to the track, and tilts its leg forward. The cycle repeats with the roles of feet 1 and 2 reversed: Foot 2 degrades its ATP to ADP and detaches from the track, and so on.

To see how kinesin motors work, let’s take it step-by-step (literally). Initially, both feet are attached to the microtubule, and one of them has bound to an ATP molecule. The ATP molecule releases its energy (turning into ADP), and this energy is used to detach the foot from the microtubule. Once this foot is detached, the molecular storm initially pushes the foot forward and backward, but it cannot go very far as the other foot is still holding on to the track. Now, the foot still planted on the track takes on an ATP molecule and by an allosteric shape change bends the whole kinesin molecule forward, forcing the dangling foot toward the forward direction. Now, the dangling foot latches on in front of the attached foot, and releases ADP. The attached foot degrades its ATP in turn, detaches from the track, and the cycle repeats (
Figure 6.9
).

We find here a mechanism that is similar to our nano-Sisyphus model: The allosteric interaction plays the role of Sisyphus, not allowing the free foot to swing backward as it is randomly pushed by the molecular storm.
Once the foot has made a step, the now lagging foot must be released in an irreversible reset step, requiring the breakdown of an ATP molecule to a lower-energy ADP molecule. As long as there is a supply of ATP molecules, the motor will keep walking.

The hallmark of a tightly coupled molecular motor is that it goes through well-defined cycles, using up a fixed number of ATP molecules during each step. Nevertheless, random motion is the drive behind the motor’s locomotion, as it ultimately moves the legs of the motor forward—of course, rectified by the allosteric interaction of the motor’s legs with ATP.

Loosely coupled motors, by contrast, rely more heavily on random motion and have no fixed-step cycle. And they are more difficult to understand.

To understand loosely coupled motors, consider two ways that nanoscale objects can move while immersed in water. We have already encountered random motion, which is caused by collisions with fast-moving water molecules. Physicists call this random motion
diffusion
(
Figure 6.10
). When a molecule moves by pure diffusion, it executes a random walk: Each step it takes is in a random direction, independent of the step it took previously. As a result, the molecule wanders around aimlessly, like a drunk after a night of binge drinking (sometimes this motion is called the
drunkard’s walk
).

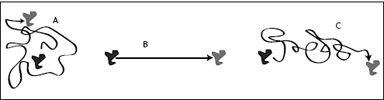
FIGURE 6.10.
Possible molecular motions: (A) Pure diffusion: The molecule moves along a random path and makes no net headway. (B) Pure drift: The molecule moves along a straight, deterministic path in the direction of an applied force. (C) Drift and diffusion: The molecule moves, on average, in the direction of the force, but superimposed is random, diffusive motion.

The other type of motion occurs when a force is applied to the molecule. The molecule is still subject to random collisions from the molecular storm, but now, it is also dragged through the molecular tempest by the applied force. Physicists call this type of motion
drift
. What kind of forces can be applied to molecules? Ultimately, all forces in the molecular realm are of electrostatic origin. Even a chemical bond is ultimately due to electrostatic attraction (although some quantum mechanics is needed to fully explain the origin of a chemical bond).

An important fact to remember is that forces drive systems toward reduced energy. If a molecule binds to another molecule, the two molecules will not initially bind perfectly to each other—there will still be some distance between them. But as soon as the molecules feel one another, their combined energy will start to reduce, and they’ll be compelled by a force of attraction. This force pulls the molecules in the direction of further energy reduction, that is, in the direction of completing the bond.

In general, molecules experience both types of motion, diffusion and drift. Drift is a deterministic motion, always in the direction of reduced energy, while diffusion adds a random component to the molecule’s path (
Figure 6.10
). Because of this randomness, the best way to describe the motion of a molecule is to use statistical mechanics. The statement “in three seconds the molecule will move five nanometers to the left” becomes nonsensical, and we can merely state the
probability
that it may have moved to this position. Physicists can calculate the probability of a molecule’s moving to a certain location by using the so-called Fokker-Planck equation (a challenging equation usually solved by computers). This equation calculates the probability of motion on the basis of the energy landscape of the molecule. The energy landscape gives a conceptual picture of the molecule’s energy as a function of position and configuration. A steep slope in the landscape—that is, a strong dip in energy for small movements of the molecule—leads to drift. This is because steep changes in energy correspond to strong forces driving the system down the energy slope. On the other hand, on the flat parts of the landscape (where changes in the molecule’s position or shape do not change energy by much), forces are negligible, and diffusion will dominate.

With this picture in mind, we can understand how the loosely coupled motor works. A loosely coupled motor is one that relies partly on random
motion (diffusion), yet is still capable of performing directed motion. It can do this if it periodically attaches and detaches to a track. When it is attached to a track, it is subject to drift and feels a force directing it to the lowest-energy position on the track. When it is detached from the track, it diffuses freely. Loose coupling doesn’t violate the second law, because detaching from the track requires free energy, which is degraded into heat. The detachment is the irreversible reset step.

How would such a machine move? We need to think of probabilities.
Figure 6.11
shows a molecular motor on a track with an asymmetric energy landscape. The energy changes more steeply in one direction than the other, forming a saw-tooth pattern (similar to the teeth of the ratchet). On such an energy landscape, the combination of drift and diffusion will increase the probability that the machine will move one way rather than the other.

The asymmetry of the track’s energy has two effects on the machine: First, the machine will spend most of its time near the energy minimum of the track. This minimum is at the lowest point of the track (
Figure 6.11
, step A). Now, when the machine detaches, it is just a short distance to the neighboring tooth on the left, but a larger distance to the tooth on the right. Second, once the motor reattaches to a random spot on the track, it will most likely end up on a gentle slope of the energy. This slope is also directed to the left, so the motor will experience a force pushing it to the left toward the minimum of the next tooth’s energy. The overall result is that the asymmetry of the track’s energy biases the motion of the motor to the left.

In
Figure 6.11
, the bottom three graphs represent this motion by plots of probability, each plot corresponding to a step in the cartoon above. Initially, if we know the motor is attached at a certain energy minimum, the probability that it is at this location is 100 percent (plot A). Then, the motor detaches and freely diffuses. This is represented by the flattened-out peak in the probability shown in plot B. When the motor reattaches, it quickly finds the nearest energy minimum. Because it was closer to the minimum to the left of its original position, the probability is somewhat higher that it ended up moving left rather than right. This represented in plot C by the slightly larger peaks in the probability to the left of the starting position. Note that the largest probability peak is at the starting position, indicating that often the motor does not move at all, but reattaches at its original location. There is also a small peak to the
right
of the starting position, indicating the small, but nonnegligible probability that the motor moves backward. On average, however, after many steps, the motor will move to the left. That is, it will perform directed motion.

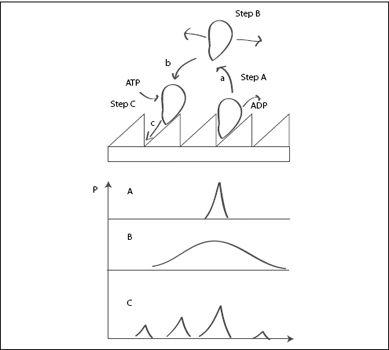
FIGURE 6.11.
Top: Motion of a loosely coupled motor. In step A, the breakdown of an ATP molecule and release of ADP detaches the motor from the track (arrow a). In step B, the motor diffuses freely. In step C, the motor reattaches (arrow b), binding ATP in the process. As it binds to the molecular track, it quickly moves to the lowest energy state by drift (arrow c). Bottom: Probability plots corresponding to the steps shown above. (A) A single probability peak corresponds to the motor initially positioned at the energy minimum (prior to detaching in step A). (B) The motor diffuses freely, leading to a broadening of the probability peak. (C) The motor reattaches. Because of the asymmetry of the track’s energy, the probability that it attaches to the left of the starting position is higher than the probability that it attaches to the right. The motor can also reattach at the same position where it started. However, leftward motion is more probable than rightward motion, and, on average, the motor will move to the left.

If this model sounds eerily similar to our ratchet in
Chapter 5
, consider that physicists refer to this type of loosely coupled machine as a
Brownian ratchet
. The Brownian ratchet, unlike Feynman’s passive ratchet, uses an irreversible step: the detachment from the track, fueled by the breakdown of an ATP molecule. We could, in fact, make Feynman’s ratchet work, if from time to time, we injected energy to loosen and then retighten the pawl’s spring. On loosening the spring, the wheel would rotate freely, with a slightly higher probability of rotating one way rather than the other. Tightening the pawl’s spring would push the wheel further in the direction we want. On average, the wheel would move forward and do work. In fact, it can be shown that
any
molecular machine that operates on an asymmetric energy landscape and incorporates an irreversible, energy-degrading step can extract useful work from the molecular storm.

Because the motion of a loosely coupled machine is dominated by diffusion, the machine can take several steps at once, but it can also move backward. Therefore, loosely coupled machines do not move as efficiently as tightly coupled machines. Moreover, they do not move along a track for long distances before completely detaching. A motor that can move long distances along a track, continuously stepping forward, is called a processive motor. Tightly coupled motors tend to be processive; loosely coupled motors are not.

As mentioned earlier, there is an ongoing battle between scientists about whether molecular motors are tightly or loosely coupled. This fight has a deeper origin: Some scientists like the idea that the randomness of thermal motion plays a major role in molecular motors, while others prefer a more deterministic view. Loosely coupled motors have a clear dependence on random motion: The actual stepping is primarily done by random diffusion, with the asymmetric energy of the track providing the needed forward
bias. Tightly coupled motors do not obviously incorporate random diffusion, so the tight-coupling mechanism is usually favored by many in the antirandomness camp.