Life's Ratchet: How Molecular Machines Extract Order from Chaos (26 page)

In a September 2000 spoof in the satirical newspaper
The Onion
, concerned voters demanded that their legislators repeal the second law of thermodynamics: “‘Why can’t disorder decrease over time instead of everything decaying?’ . . . ‘Is that too much to ask? This is our children’s future we’re talking about!’” If the second law were a dogma imposed by nefarious physicists, Congress might tell us to get rid of it. But we are not that powerful (conspiracy theories about evil scientists notwithstanding). The second law is an
inescapable
(macroscopic) consequence of the randomizing power of the
inescapable
(microscopic) molecular storm.

As explained by physicists Dean Astumian and Peter Hänggi in their 2002
Physics Today
article on Brownian motors, a typical molecular motor uses about 100 to 1,000 ATP molecules per second. This translates into performing work at a rate of only 10
⁻¹⁶
watts (1 watt = 1 joule/second). It would take 10
²¹
molecular motors to generate as much power as a typical car engine—an unimaginably large number. Yet, this number of molecular machines barely fills a teaspoon—a teaspoon that could generate 130 horsepower! The power density of molecular machines (the power generated per volume the machine occupies) is very large, about 10
⁸
watts per cubic meter. A car engine has a power density that is a thousand times smaller. These little machines are extremely efficient: As mentioned earlier, our entire bodies, which are based on these machines, operate on a power “budget” of just 100 watts, the same as a (large) incandescent light bulb.

If that were not astonishing enough, consider the world these machines inhabit. At the nanoscale, nothing can escape the molecular storm. As Astumian and Hänggi point out, every molecular machine in our bodies is hit by a fast-moving water molecule about every 10
⁻¹³
seconds. Each collision delivers on average 4.3 × 10
⁻²¹
joules of energy (the energy is determined by the product of Boltzmann’s constant and body temperature measured in degree Kelvin). This translates into an average power input of more than 10
⁻⁸
watts. Remember that a molecular machine generates only about 10
⁻¹⁶
watts in power. Thus, the power input from the random pounding of water molecules is a hundred million times larger than the power output of our machine! To put this into perspective, compare this to a car in a windstorm. How powerful would a storm need to be to transfer a hundred million times more power to a car than the car’s engine can generate? Taking the air resistance of a car into account, the storm would need a wind speed of an astounding seventy thousand miles per hour to have the same effect that the molecular storm has on our hapless molecular machines! I doubt even a Hummer would get very far against a storm like that.

An important difference between a macroscopic storm and our molecular storm is that the molecular storm has no preferred direction. In other words, every collision with a water molecule comes from a random direction. Storms of our everyday experience blow in a more or less constant direction and can perform useful work (for example, move a sailboat or a windmill). At the nanoscale, not only is the molecular storm an overwhelming force, but it is also completely random. It is difficult to imagine how a molecular storm can serve as an energy source for useful work.

What to do? We can think of two possibilities. We could build an incredibly robust machine, a kind of molecular super-Hummer, which could make small, measured steps while resisting the thermal chaos surrounding it. Alternatively, we could make a “floppy” machine that works according to the motto “If you can’t beat ’em, join ’em.” That is, make a machine that could “harvest” favorable pushes from the random hits it receives. Since the latter was our approach in
Chapter 5
and has so far failed miserably, it may be tempting to go with the first option. But the super-Hummer
option would clearly not work, either. Such a molecular machine would need to be made exceedingly “stiff” to withstand the molecular storm. If it were that stiff, how could it move at all? As soon as it wanted to move, it would have to weaken its springs. But if the springs were weakened, the machine would be pushed around in the storm just as before. Moreover, where does motion come from in the first place? As we have seen, the only motion existing at the molecular scale
is
the molecular storm. How could a molecular machine move, while resisting this motion?

Let’s stick with the notion that our machine must somehow tame the molecular storm, regardless of whether the machine is robust or floppy. To understand how molecular machines tame the chaos of thermal motion, we first need to learn what these machines actually look like. Obviously, they are not truly the ratchets or car engines we used as convenient analogies. To describe molecular machines, we need to learn a little bit of biochemistry.

Molecular machines must change their shapes to create locomotion. How is this possible? A good starting point is to look at chemical reactions: In chemical reactions, molecules must change shape to combine in novel ways. These changes in shape are driven by a reduction in free energy.

If this were all there were to driving chemical reactions, they would happen in a snap. Yet, many chemical reactions take time. Your car does not turn into a pile of rust overnight, and your milk does not curdle as soon as you open the carton. The speed of chemical reactions is explained by the concept of
activation energy
. During any chemical reaction, there is an awkward moment when molecules no longer have their original shapes, but neither do they have their final shapes. They form an intermediate state between their initial state (reactants) and their final state (products). This intermediate state, called the
transition state
, tends to be uncomfortable for the molecules.

Figure 6.1
illustrates the transition state with the closing of a cardboard box. One way to close a cardboard box is to overlap each of the four flaps with a neighboring flap. When I try to do this, there is always a tricky moment when I am trying to push down all four flaps at once—one always pops out. But once I’ve succeeded, the box is perfectly happy and shut.
Thus we have two comfortable (low-energy) states. Initial state: box (and flaps) open; final state: box closed. To get from one state to the other, we have to cross an intermediate uncomfortable, high-energy state (shown as a question mark in the figure).

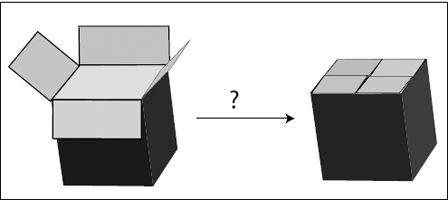
FIGURE 6.1.
Folding a cardboard box to close it. Both the open and the closed box are stable states, but to get from one to the other, we need to push all four flaps together at once, an often quite unstable and awkward state of the system.

The same holds true for chemical reactions. As reactants turn into products, chemical bonds become strained for a moment before the molecules relax into their final shapes. This strained state has higher energy than either the original or the final state of the transformation. In
Figure 6.2
, two molecules are not quite compatible, but are “trying” to combine and form a new compound molecule with lower energy. The two molecules can lower their energy if they combine, but first they need to obtain enough energy to pass over the transition state. In the cardboard box example, I needed to push the flaps down with enough force so they snapped into place. In other words, I needed to supply sufficient energy to get past the awkward arrangement of the four flaps pushing against each other. In chemistry, the energy required to cross over the transition state is called the
activation energy
. It is the minimum amount of energy required to activate a chemical reaction.

Where do molecules obtain the needed activation energy? From the molecular storm! The impetus needed to make it across the transition state is provided by small, fast molecules (typically water molecules) fortuitously colliding with the reacting molecules to give them the right push. If lucky, the push causes the molecules to snap into their new shapes. Of
course, not every colliding water molecule will have enough energy or hit the reacting molecules in the right way. Chemical reactions take time— we have to wait for the right push to come along, and the higher the activation energy needed, the more time it takes, as higher-energy collisions are much less frequent than low-energy collisions.

What determines the height of the activation barrier? In a nutshell, it depends on how uncomfortable the molecules become as they transform from the initial to the final state. If I try to change a molecule by rearranging several of its bonds, it will take a lot of bending and twisting, and activation energy will be high. On the other hand, if a tiny rearrangement of one atom will do, activation energy may be low.

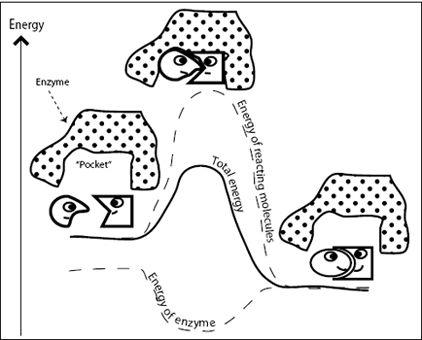
Many important chemical reactions in cells require enormously large activation energy. These transformations proceed at such a glacial pace we’d probably be dead before our cells cycled through them even once. To solve this problem, nature has invented a neat trick. Let’s imagine a helper molecule whose job is to make the transition state more comfortable and therefore lower the activation energy (
Figure 6.3
). If the activation energy is lowered, the reaction rate increases. Such helpful molecules are called enzymes, and their involvement speeds up reactions by many orders of magnitude. Enzymes are biological catalysts, comparable to your car’s catalytic converter, which speeds up the oxidation of harmful exhaust gases.

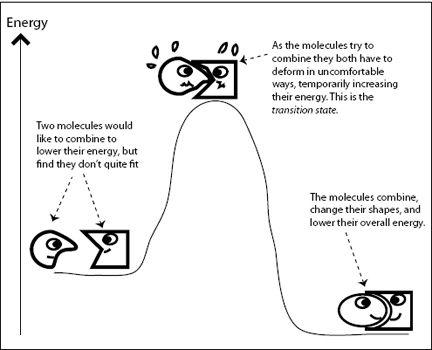
FIGURE 6.2.
Chemical reactions proceed via “uncomfortable” transition states.

Enzymes have a pocket that is custom-made to fit the substrate (the reactant molecules). Initially, when the substrate binds into the enzyme’s pocket, it is not a perfect fit, but as the enzyme and the substrate slightly change shape and begin to fit more comfortably, the enzyme pushes the substrate toward the transition state. Once the substrate is in the transition state, the enzyme is happy (at lower energy), and the total energy of the system (the energy of the transition state plus the energy of the enzyme) is reduced (
Figure 6.3
). Because the transition state still has higher energy than the final, product state, the transition state has no choice but to convert to the product. The product is uncomfortable in the enzyme’s pocket and is released. The enzyme snaps back to its old shape and is ready to take on a new substrate for conversion.