In Pursuit of the Unknown (52 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

We can take advantage of this by encoding the same information more efficiently. If 0 occurs with probability 9/10 and 1 with probability 1/10, we can define a new code like this:
000 â 00 (use whenever possible)
00 â 01 (if no 000 remains)
0 â 10 (if no 00 remains)
1 â 11 (always)
What I mean here is that a message such as
00000000100010000010000001000000000
is first broken up from left to right into blocks that read 000, 00, 0, or 1. With strings of consecutive 0s, we use 000 whenever we can. If not, what's left is either 00 or 0, followed by a 1. So here the message breaks up as
000-000-00-1-000-1-000-00-1-000-000-1-000-000-000
and the coded version becomes
00-00-01-11-00-11-00-01-11-00-00-11-11-00-00-00
The original message has 35 digits, but the encoded version has only 32. The amount of information seems to have decreased.
Sometimes the coded version might be longer: for instance, 111 turns into 111111. But that's rare because 1 occurs only one time in ten on average. There will be quite a lot of 000s, which drop to 00. Any spare 00 changes to 01, the same length; a spare 0 increases the length by changing
to 00. The upshot is that in the long run, for randomly chosen messages with the given probabilities of 0 and 1, the coded version is shorter.
My code here is very simple-minded, and a cleverer choice can shorten the message even more. One of the main questions that Shannon wanted to answer was: how efficient can codes of this general type be? If you know the list of symbols that is being used to create a message, and you also know how likely each symbol is, how much can you shorten the message by using a suitable code? His solution was an equation, defining the amount of information in terms of these probabilities.
Suppose for simplicity that the messages use only two symbols 0 and 1, but now these are like flips of a biased coin, so that 0 has probability
p
of occurring, and 1 has probability
q
= 1 â
p
. Shannon's analysis led him to a formula for the information content: it should be defined as
H
= â
p
log
p
â
q
log
q
where log is the logarithm to base 2.
At first sight this doesn't seem terribly intuitive. I'll explain how Shannon derived it in a moment, but the main thing to appreciate at this stage is how
H
behaves as
p
varies from 0 to 1, which is shown in
Figure 56
. The value of
H
increases smoothly from 0 to 1 as
p
rises from 0 to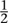 , and then drops back symmetrically to 0 as
, and then drops back symmetrically to 0 as
p
goes from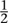 to 1.
to 1.
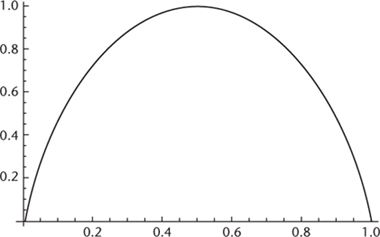
Fig 56
How Shannon information
H
depends on
p
.
H
runs vertically and p runs horizontally.
Shannon pointed out several âinteresting properties' of
H
, so defined:
â¢
If
p
= 0, in which case only the symbol 1 will occur, the information
H
is
zero. That is, if we are certain which symbol is going to be transmitted to us, receiving it conveys no information whatsoever.
â¢
The same holds when
p
= 1. Only the symbol 0 will occur, and again we receive no information.
â¢
The amount of information is largest when
p
=
q
=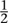 , corresponding to the toss of a fair coin. In this case,
, corresponding to the toss of a fair coin. In this case,
H
= â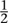 log
log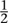 â
â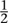 log
log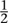 = â log
= â log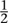 = 1
= 1
bearing in mind that the logarithms are to base 2. That is, one toss of a fair coin conveys one bit of information, as we were originally assuming before we started worrying about coding messages to compress them, and biased coins.
â¢
In all other cases, receiving one symbol conveys
less
information than one bit.
â¢
The more biased the coin becomes, the less information the result of one toss conveys.
â¢
The formula treats the two symbols in exactly the same way. If we exchange
p
and
q
, then
H
stays the same.
All of these properties correspond to our intuitive sense of how much information we receive when we are told the result of a coin toss. That makes the formula a reasonable working definition. Shannon then provided a solid foundation for his definition by listing several basic principles that any measure of information content ought to obey and deriving a unique formula that satisfied them. His set-up was very general: the message could choose from a number of different symbols, occurring with probabilities
p
1
,
p
2
, . . .,
p
n
where
n
is the number of symbols. The information
H
conveyed by a choice of one of these symbols should satisfy:
