In Pursuit of the Unknown (48 page)
Read In Pursuit of the Unknown Online
Authors: Ian Stewart

Fig 54
Wave packet.
The equation bears the name of Erwin Schrödinger. In 1927, building on the work of several other physicists, notably Werner Heisenberg, he wrote down a differential equation for any quantum wave function. It looked like this:
Here Ψ(Greek capital psi) is the form of the wave,
t
is time (so
â/ât
applied to Ψ gives its rate of change with respect to time),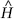 is an expression called the Hamiltonian operator, and
is an expression called the Hamiltonian operator, and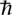 is
is
h
/2Ï, where
h
is Planck's constant. And i? That was the weirdest feature of all. It's the square root of minus one (
Chapter 5
). Schrödinger's equation applies to waves defined over the
complex
numbers, not just the real numbers as in the familiar wave equation.
Waves in what? The classical wave equation (
Chapter 8
) defines waves in space, and its solution is a numerical function of space and time. The same goes for Schrödinger's equation, but now the wave function Ψ takes complex values, not just real ones. It's a bit like an ocean wave whose
height is 2 + 3i. The appearance of i is in many ways the most mysterious and profound feature of quantum mechanics. Previously i had turned up in solutions of equations, and in methods for finding those solutions, but here it was part of the equation, an explicit feature of the physical law.
One way to interpret this is that quantum waves are linked pairs of real waves, as if my complex ocean wave were really two waves, one of height 2 and the other of height 3, with the two directions of height at right angles to each other. But it's not quite that straightforward, because the two waves don't have a fixed shape. As time passes, they cycle through a whole series of shapes, and each is mysteriously linked to the other. It's a bit like the electric and magnetic components of a light wave, but now electricity can and does ârotate' into magnetism, and conversely. The two waves are two facets of a single shape, which spins steadily around the unit circle in the complex plane. Both the real and the imaginary parts of this rotating shape change in a very specific way: they are combined in sinusoidally varying amounts. Mathematically this leads to the idea that a quantum wave function has a special kind of
phase
. The physical interpretation of that phase is similar to, but different from, the role of phase in the classical wave equation.
Remember how Fourier's trick solves both the heat equation and the wave equation? Some special solutions, Fourier's sines and cosines, have especially pleasant mathematical properties. All other solutions, however complicated, are superpositions of these normal modes. We can solve Schrödinger's equation using a similar idea, but now the basic patterns are more complicated than sines and cosines. They are called eigenfunctions, and they can be distinguished from all other solutions. Instead of being some general function of both space and time, an eigenfunction is a function defined only on space, multiplied by one depending only on time. The space and time variables, in the jargon, are separable. The eigenfunctions depend on the Hamiltonian operator, which is a mathematical description of the physical system concerned. Different systems â an electron in a potential well, a pair of colliding photons, whatever â have different Hamiltonian operators, hence different eigenfunctions.
For simplicity, consider a standing wave for the classical wave equation â a vibrating violin string, whose ends are pinned down. At all instants of time, the shape of the string is almost the same, but the amplitude is modulated: multiplied by a factor that varies sinusoidally with time, as in
Figure 35
(page 138). The complex phase of a quantum wave function is similar, but harder to visualise. For any individual eigenfunction, the effect
of the quantum phase is just a shift of the time coordinate. For a superposition of several eigenfunctions, you split the wave function into these components, factor each into a purely spatial part times a purely temporal one, spin the temporal part round the unit circle in the complex plane at the appropriate speed, and add the pieces back together. Each separate eigenfunction has a complex amplitude, and this modulates at its own particular frequency.
It may sound complicated, but it would be completely baffling if you didn't split the wave function into eigenfunctions. At least then you've got a chance.
Despite these complexities, quantum mechanics would be just a fancy version of the classical wave equation, resulting in two waves rather than one, were it not for a puzzling twist. You can observe classical waves, and see what shape they are, even if they are superpositions of several Fourier modes. But in quantum mechanics, you can never observe the entire wave function. All you can observe on any given occasion is a single component eigenfunction. Roughly speaking, if you attempt to measure two of these components at the same time, the measurement process on one of them disturbs the other one.
This immediately raises a difficult philosophical issue. If you can't observe the entire wave function, does it actually exist? Is it a genuine physical object, or just a convenient mathematical fiction? Is an unobservable quantity scientifically meaningful? It is here that Schrödinger's celebrated feline enters the story. It arises because of a standard way to interpret what a quantum measurement is, called the Copenhagen interpretation.
1
Imagine a quantum system in some superposed state: say, an electron whose state is a mixture of spin-up and spin-down, which are pure states defined by eigenfunctions. (It doesn't matter what spin-up and spin-down mean.) When you observe the state, however, you either get spin-up, or you get spin-down. You can't observe a superposition. Moreover, once you've observed one of these â say spin-up â that
becomes
the actual state of the electron. Somehow your measurement seems to have forced the superposition to change into a specific component eigenfunction. This Copenhagen interpretation takes this statement literally: your measurement process has
collapsed
the original wave function into a single pure eigenfunction.
If you observe a lot of electrons, sometimes you get spin-up, sometimes
spin-down. You can infer the probability that the electron is in one of those states. So the wave function itself can be interpreted as a kind of probability cloud. It doesn't show the actual state of the electron: it shows how probable it is that when you measure it, you get a particular result. But that makes it a statistical pattern, not a real
thing
. It no more proves the wave function is real than Quetelet's measurements of human height prove that a developing embryo possesses some sort of bell curve.
The Copenhagen interpretation is straightforward, reflects what happens in experiments, and makes no detailed assumptions about what happens when you observe a quantum system. For these reasons, most working physicists are very happy to use it. But some were not, in the early days when they theory was still being thrashed out, and some still are not. And one of the dissenters was Schrödinger himself.
In 1935, Schrödinger was worrying about the Copenhagen interpretation. He could see that it worked, on a pragmatic level, for quantum systems like electrons and photons. But the world around him, even though deep down inside it was just a seething mass of quantum particles, seemed different. Seeking a way to make the difference as glaring as he could, Schrödinger came up with a thought experiment in which a quantum particle had a dramatic and obvious effect on a cat.
Imagine a box, which when shut is impervious to all quantum interactions. Inside it, place an atom of radioactive matter, a radiation detector, a flask of poison, and a live cat. Now shut the box, and wait. At some point the radioactive atom will decay, and emit a particle of radiation. The detector will spot it, and is rigged so that when it does so, it causes the flask to break and release the poison inside. This kills the cat.
In quantum mechanics, the decay of a radioactive atom is a random event. From outside, no observer can tell whether the atom has decayed or not. If it has, the cat is dead; if not, it's alive. According to the Copenhagen interpretation, until someone observes the atom, it is in a superposition of two quantum states: decayed and not decayed. The same goes for the states of the detector, the flask, and the cat. So the cat is in a superposition of two states: dead and alive.
Since the box is impervious to all quantum interactions, the only way to find out whether the atom has decayed and killed the cat is to open the box. The Copenhagen interpretation tells us that the instant we do this, the wave functions collapse and the cat suddenly switches to a pure state: either dead, or alive. However, the inside of the box is no different from the
external world, where we never observe a cat that is in a superposed alive/dead state. So before we open the box and observe its contents, there must either be a dead cat inside, or a live one.
Schrödinger intended this thought experiment as a criticism of the Copenhagen interpretation. Microscopic quantum systems obey the superposition principle and can exist in mixed states; macroscopic ones can't. By linking a microscopic system, the atom, to a macroscopic one, the cat, Schrödinger was pointing out what he believed to be a flaw in the Copenhagen interpretation: it gave nonsense when applied to a cat. He must have been startled when the majority of physicists responded, in effect: âYes, Erwin, you're absolutely right: until someone opens the box, the cat really is simultaneously dead and alive.' Especially when it dawned on him that he couldn't find out who was right, even if he opened the box. He would observe either a live cat or a dead one. He might infer that the cat had been in that state before he opened the box, but he couldn't be sure. The observable result was consistent with the Copenhagen interpretation.
Very well: add a film camera to the contents of the box, and film what actually happens. That will decide the matter. âAh, no,' the physicists replied. âYou can only see what the camera has filmed after you open the box. Before that, the film is in a superposed state: containing a movie of a live cat, and containing a movie of a dead one.'
The Copenhagen interpretation freed up physicists to do their calculations and sort out what quantum mechanics predicted, without facing up to the difficult, if not impossible, issue of how the classical world emerged from a quantum substrate â how a macroscopic device, unimaginably complex on a quantum scale, somehow made a measurement of a quantum state. Since the Copenhagen interpretation did the job, they weren't really interested in philosophical questions. So generations of physicists were taught that Schrödinger had invented his cat to show that quantum superposition extended into the macroscopic world too: the exact opposite of what Schrödinger had been trying to tell them.
