In Pursuit of the Unknown (43 page)

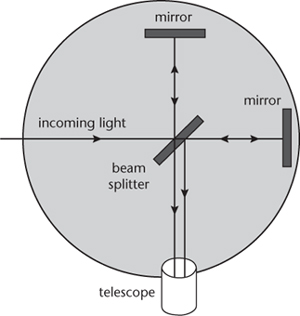
Fig 48
The Michelson-Morley experiment.

It was a careful, accurate experiment. Its result was entirely negative. The fringes did not move by 40% of their width. As far as anyone could tell with certainty, they didn't move at all. Later experiments, capable of detecting a shift 0.07% as wide as a fringe, also gave a negative result. The ether did not exist.

This result didn't just dispose of the ether: it threatened to dispose of Maxwell's theory of electromagnetism, too. It implied that light does not behave in a Newtonian manner, relative to moving frames of reference. This problem can be traced right back to the mathematical properties of Maxwell's equations and how they transform relative to a moving frame. The Irish physicist and chemist George FitzGerald and the Dutch physicist Hendrik Lorenz independently suggested (in 1892 and 1895 respectively) an audacious way to get round the problem. If a moving body contracts slightly in its direction of motion, by just the right amount, then the
change in phase that the Michelson–Morley experiment was hoping to detect would be exactly cancelled out by the change in the length of the path that the light was following. Lorenz showed that this ‘Lorenz–FitzGerald contraction' sorted out the mathematical difficulties with the Maxwell equations as well. The joint discovery showed that the results of experiments on electromagnetism, including light, do not depend on the relative motion of the reference frame. Poincaré, who had also been working along similar lines, added his persuasive intellectual weight to the idea.

The stage was now set for Einstein. In 1905 he developed and extended previous speculations about a new theory of relative motion in a paper ‘On the electrodynamics of moving bodies'. His work went beyond that of his predecessors in two ways. He showed that the necessary change to the mathematical formulation of relative motion was more than just a trick to sort out electromagnetism. It was required for all physical laws. It followed that the new mathematics must be a genuine description of reality, with the same philosophical status that had been accorded to the prevailing Newtonian description, but providing a better agreement with experiments. It was real physics.

The view of relative motion employed by Newton went back even further, to Galileo. In his 1632
Dialogo sopra i due massimi sistemi del mondo
(‘Dialogue Concerning the Two Chief World Systems') Galileo discussed a ship travelling at constant velocity on a perfectly smooth sea, arguing that no experiment in mechanics carried out below decks could reveal that the ship was moving. This is Galileo's principle of relativity: in mechanics, there is no difference between observations made in two frames that are moving with uniform velocity relative to each other. In particular, there is no special frame of reference that is ‘at rest'. Einstein's starting-point was the same principle, but with an extra twist: it must apply not just to mechanics, but to all physical laws. Among them, of course, being Maxwell's equations and the constancy of the speed of light.

To Einstein, the Michelson–Morley experiment was a small piece of extra evidence, but it wasn't proof of the pudding. The proof that his new theory was correct lay in his extended principle of relativity, and what it implied for the mathematical structure of the laws of physics. If you accepted the principle, all else followed. This is why the theory became known as ‘relativity'. Not because ‘everything is relative', but because you
have to take into account the
manner
in which everything is relative. And it's not what you expect.

This version of Einstein's theory is known as special relativity because it applies only to frames of reference that are moving uniformly with respect to each other. Among its consequences are the Lorenz–FitzGerald contraction, now interpreted as a necessary feature of space-time. In fact, there were three related effects. If one frame of reference is moving uniformly relative to another one, then lengths measured in that frame contract along the direction of motion, masses increase, and time runs more slowly. These three effects are tied together by the basic conservation laws of energy and momentum; once you accept one of them, the others are logical consequences.

The technical formulation of these effects is a formula that describes how measurements in one frame relate to those in the other. The executive summary is: if a body could move close to the speed of light, then its length would become very small, time would slow to a crawl, and its mass would become very large. I'll just give a flavour of the mathematics: the physical description should not be taken too literally and it would take too long to set it up in the correct language. It all comes from. . . Pythagoras's theorem. One of the oldest equations in science leads to one of the newest.

Suppose that a spaceship is passing overhead with velocity v, and the crew performs an experiment. They send a pulse of light from the floor of the cabin to the roof, and measure the time taken to be T. Meanwhile an observer on the ground watches the experiment through a telescope (assume the spaceship is transparent), measuring the time to be
t
.

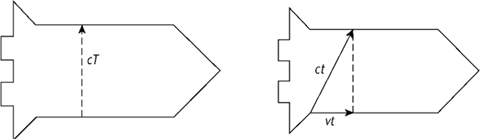
Fig 49
Left
: The experiment in the crew's frame of reference.
right
: The same experiment in the ground observer's frame of reference. Grey shows the ship's position as seen from the ground when the light beam starts its journey; black shows the ship's position when the light completes its journey.

Figure 49
(
left
) shows the geometry of the experiment from the crew's point of view. To them, the light has gone straight up. Since light travels at
speed
c
, the distance travelled is
cT
, shown by the dotted arrow.
Figure 49
(
right
) shows the geometry of the experiment from the ground observer's point of view. The spaceship has moved a distance
vt
, so the light has travelled diagonally. Since light
also
travels at speed
c
for the ground observer, the diagonal has length
ct
. But the dotted line has the same length as the dotted arrow in the first picture, namely
cT
. By Pythagoras's theorem,

(
ct
)
²
= (
CT
)
²
+ (
vt
)
²

We solve for
T
, getting

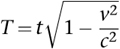
which is smaller than
t
.

To derive the Lorenz-FitzGerald contraction, we now imagine that the spaceship travels to a planet distance
x
from Earth at speed v. Then the elapsed time is
t
=
x/v
. But the previous formula shows that to the crew, the time taken is T, not
t
. For them, the distance
X
must satisfy
T
=
X/v
. Therefore

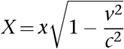
which is smaller than
x
.

The derivation of the mass change is slightly more involved, and it depends on a particular interpretation of mass, ‘rest mass', so I won't give details. The formula is

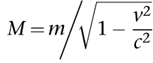
which is larger than
m
.

These equations tell us that there is something very special about the speed of light (and indeed about light). An important consequence of this formalism is that the speed of light is an impenetrable barrier. If a body starts out slower than light, it cannot be accelerated to a speed greater than that of light. In September 2011 physicists working in Italy announced that subatomic particles called neutrinos appeared to be travelling faster than light.
¹
Their observation is controversial, but if it is confirmed, it will lead to important new physics.

Pythagoras turns up in relativity in other ways. One is the formulation
of special relativity in terms of the geometry of space-time, originally introduced by Hermann Minkowski. Ordinary Newtonian space can be captured mathematically by making its points correspond to three coordinates (
x
,
y
,
z
), and defining the distance
d
between such a point and another one (
X
,
Y
,
Z
) using Pythagoras's theorem:

d
²
= (
x
–
X
)
²
+ (
y
–
Y
)
²
+ (
z
–
Z
)
²

Now take the square root to get
d
. Minkowski space-time is similar, but now there are four coordinates (
x, y, z, t
), three of space plus one of time, and a point is called an
event
– a location in space, observed at a specified time. The distance formula is very similar: