In Pursuit of the Unknown (12 page)

The idea at the heart of calculus is to approximate the rate of change of a function over a small interval
h
, and then take the limit as
h
tends to zero. For a general function
y
=
f
(
x
) this procedure leads to the equation that decorates the opening of this chapter, but using a general variable
x
instead of time:

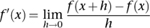
In the numerator we see the change in
f
; the denominator is the change in
x
. This equation defines the derivative
f
′(
x
) uniquely, provided the limit exists. That has to be proved for any function under consideration: the limit does exist for most of the standard functions – squares, cubes, higher powers, logarithms, exponentials, trigonometric functions.

Nowhere in the calculation do we ever divide by zero, because we never set
h
= 0. Moreover, nothing here actually flows. What matters is the range of values that
h
can assume, not how it moves through that range. So Berkeley's sarcastic characterisation is actually spot on. The limit
L
is the ghost of the departed quantity – my
h
, Newton's
o
. But the manner of the quantity's departure –
approaching
zero, not
reaching
it – leads to a perfectly sensible and logically well-defined ghost.

Calculus now had a sound logical basis. It deserved, and acquired, a new name to reflect its new status: analysis.

 

It is no more possible to list all the ways that calculus can be applied than it is to list everything in the world that depends on using a screwdriver. On a simple computational level, applications of calculus include finding lengths of curves, areas of surfaces and complicated shapes, volumes of solids, maximum and minimum values, and centres of mass. In conjunction with the laws of mechanics, calculus tells us how to work
out the trajectory of a space rocket, the stresses in rock at a subduction zone that might produce an earthquake, the way a building will vibrate if an earthquake hits, the way a car bounces up and down on its suspension, the time it takes a bacterial infection to spread, the way a surgical wound heals, and the forces that act on a suspension bridge in a high wind.

Many of these applications stem from the deep structure of Newton's laws: they are models of nature stated as differential equations. These are equations involving derivatives of an unknown function, and techniques from calculus are needed to solve them. I will say no more here, because every chapter from
Chapter 8
onwards involves calculus explicitly, mainly in the guise of differential equations. The sole exception is
Chapter 15
on information theory, and even there other developments that I don't mention also involve calculus. Like the screwdriver, calculus is simply an indispensable tool in the engineer's and scientist's toolkits. More than any other mathematical technique, it has created the modern world.

It determines the force of gravitational attraction between two bodies in terms of their masses and the distance between them.

It can be applied to any system of bodies interacting through the force of gravity, such as the Solar System. It tells us that their motion is determined by a simple mathematical law.

Accurate prediction of eclipses, planetary orbits, the return of comets, the rotation of galaxies. Artificial satellites, surveys of the Earth, the Hubble telescope, observations of solar flares. Interplanetary probes, Mars rovers, satellite communications and television, the Global Positioning System.

N
ewton's laws of motion capture the relationship between the forces that act on a body and how it moves in response to those forces. Calculus provides mathematical techniques for solving the resulting equations. One further ingredient is needed to apply the laws: specifying the forces. The most ambitious aspect of Newton's
Principia
was to do precisely that for the bodies of the Solar System – the Sun, planets, moons, asteroids, and comets. Newton's law of gravitation synthesised, in one simple mathematical formula, millennia of astronomical observations and theories. It explained many puzzling features of planetary motion, and made it possible to predict the future movements of the Solar System with great accuracy. Einstein's theory of general relativity eventually superseded the Newtonian theory of gravity, as far as fundamental physics is concerned, but for almost all practical purposes the simpler Newtonian approach still reigns supreme. Today the world's space agencies, such as NASA and ESA, still use Newton's laws of motion and gravitation to work out the most effective trajectories for spacecraft.

It was Newton's law of gravitation, above all else, that justified his subtitle:
The System of the World
. This law demonstrated the enormous power of mathematics to find hidden patterns in nature and to reveal hidden simplicities behind the world's complexities. And in time, as mathematicians and astronomers asked harder questions, to reveal the hidden complexities implicit in Newton's simple law. To appreciate what Newton achieved, we must first go back in time, to see how previous cultures viewed the stars and planets.

 

Humans have been watching the night sky since the dawn of history. Their initial impression would have been a random scattering of bright points of light, but they would soon have noticed that across this background the glowing orb of the Moon traced a regular path, changing shape as it did so. They would also have seen that most of those tiny bright specks of light remain in the same relative patterns, which we now call constellations. Stars move across the night sky, but they move as a single rigid unit, as if
the constellations are painted on the inside of a gigantic, rotating bowl.
¹
However, a small number of stars behave quite differently: they seem to wander around the sky. Their paths are quite complicated, and some appear to loop back on themselves from time to time. These are the planets, a word that comes from the Greek for ‘wanderer'. The ancients recognised five of them, now called Mercury, Venus, Mars, Jupiter, and Saturn. They move relative to the fixed stars at different speeds, with Saturn being the slowest.

Other celestial phenomena were even more puzzling. From time to time a comet would appear, as if from nowhere, trailing a long, curved tail. ‘Shooting stars' would seem to fall from the heavens, as if they had become detached from their supporting bowl. It is no wonder that early humans attributed the irregularities of the heavens to the caprices of supernatural beings.

The regularities could be summed up in terms so obvious that few would ever dream of disputing them. The Sun, stars, and planets revolve around a stationary Earth. That's what it looks like, that's what it feels like, so that's how it must be. To the ancients, the cosmos was geocentric – Earth-centred. One lone voice disputed the obvious: Aristarchus of Samos. Using geometrical principles and observations, Aristarchus calculated the sizes of the Earth, the Sun, and the Moon. Around 270
BC
he put forward the first heliocentric theory: the Earth and planets revolve round the Sun. His theory quickly fell out of favour and was not revived for nearly 2000 years.

By the time of Ptolemy, a Roman who lived in Egypt around 120
AD
, the planets had been tamed. Their movements were not capricious, but predictable. Ptolemy's
Almagest
(‘Great Treatise') proposed that we live in a geocentric universe in which everything literally revolves around humanity in complex combinations of circles called epicycles, supported by giant crystal spheres. His theory was wrong, but the motions that it predicted were sufficiently accurate for the errors to remain undetected for centuries. Ptolemy's system had an additional philosophical attraction: it represented the cosmos in terms of perfect geometric figures – spheres and circles. It continued the Pythagorean tradition. In Europe, the Ptolemaic theory remained unchallenged for 1400 years.

While Europe dawdled, new scientific advances were being made elsewhere, especially in Arabia, China, and India. In 499 the Indian astronomer Aryabhata put forward a mathematical model of the Solar System in which the Earth spun on its axis and the periods of planetary orbits were stated relative to the position of the Sun. In the Islamic world,
Alhazen wrote a stinging criticism of the Ptolemaic theory, though this was probably not focused on its geocentric nature. Around 1000 Abu Rayhan Biruni gave serious consideration to the possibility of a heliocentric Solar System, with the Earth spinning on its axis, but eventually plumped for the orthodoxy of the time, a stationary Earth. Around 1300, Najm al-Din al-Qazwini al-Katibi proposed a heliocentric theory, but soon changed his mind.

The big breakthrough came with the work of Nicolaus Copernicus, published in 1543 as
De Revolutionibus Orbium Coelestium
(‘On the Revolutions of the Celestial Spheres'). There is evidence, notably the occurrence of almost identical diagrams labelled with the same letters, to suggest that Copernicus was, to say the least, influenced by al-Katibi, but he went much further. He set out an explicitly heliocentric system, argued that it fitted the observations better and more economically than Ptolemy's geocentric theory did, and laid out some of the philosophical implications. Paramount among them was the novel thought that humans were not at the centre of things. The Christian Church viewed this suggestion as contrary to doctrine and did its best to discourage it. Explicit heliocentrism was heresy.

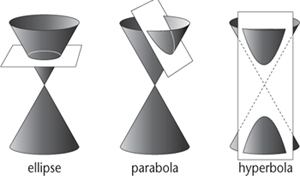
Fig 13
Conic sections.

It prevailed nevertheless, because the evidence was so strong. New and better heliocentric theories appeared. Then the spheres were thrown away altogether, in favour of a different shape from classical geometry: the ellipse. Ellipses are oval shapes, and indirect evidence suggests they were first studied in Greek geometry by Menaechmus around 350
BC
, along with hyperbolas and parabolas, as sections of a cone,
Figure 13
. Euclid is said to have written four books on conic sections, though nothing has survived if he did, and Archimedes investigated some of their properties. Greek research on the topic reached its climax in about 240
BC
with the eight-volume
Conic Sections
by Apollonius of Perga, who found a way to define
these curves purely within a plane, avoiding the third dimension. However, the Pythagorean view that circles and spheres attained a higher degree of perfection than ellipses and other more complex curves persisted.