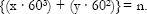Grid of the Gods (57 page)
Authors: Joseph P. Farrell,Scott D. de Hart

a) The geographical coding, elaborated by Carl Munck, Graham Hancock, and other capable Grid researchers, that discloses that Giza and its Great Pyramid were used as a prime meridian.
i) Additionally, as Thom, Munck, and others have also pointed out, use of English imperial measures also seems to have been at work in the measuring and
positioning of some of these sites long before the system was actually “English;”
8
b) The esoterical numerical coding, embodied in at least three distinct ways:
i) The emergence of number itself as
functions
of the topological metaphor, as in the examination of the topological metaphor conducted by R.A. Schwaller de Lubicz in conjunction with the Egyptian version of the metaphor;
ii) The use of numerical codes in the Platonic, Pythagorean, and Vedic tradition to denote not only certain gods in their respective pantheons, but also as
musical
codes to denote various schemes of tuning, and the use of these codes in turn to denote the astrological and astronomical data of the celestial “music of the spheres;” and,
iii) The use of gematria, or numerical coding in texts.From all these esoteric points of view, once again, the tradition tends to view pyramidal structures as the primordial mounds of “the first time” whence creation in all its diversity emerges. They are, so to speak, the metaphorical phallic symbols of that disconcerting image of androgyny one also so often encounters in the ancient cosmologies.
c) The strictly
scientific
numerical encoding, which occurred, as was seen, at two levels in the same structures:
i) Codes referring to
macrocosmic
processes, or to the physics of large systems, that is to say, encoded astronomical data; and,
ii) Codes referring to
microcosmic
processes, or to the physics of small systems, that is to say, encoded numerical data of
quantum mechanics
in the form of references to the coefficients of the constants of quantum mechanics, or, in the case of the Pythagorean tectratys, the four “elements” or forces
of the standard model of physics, the electromagnetic, gravitational, and the strong and the weak nuclear forces. Such knowled ge could only come down fdrom a civilization in High Antiquity with a similar or greater pitch of scientific development as our own. In this, we are indeed looking at the presence of alchemical machines in the proper sense, for if these ancient structures such as Nabta Playa can only reveal their secrets in accordance with a certain level of scientific sophistication, then indeed it becomes possible that other such codes await to be unlocked in these structures as our own scientific knowledge advances; it is thus possible that some of these sites on the world Grid will thus
provoke
a transformation and expansion of consciousness by actually yielding scientific information as yet unknown, if they can but be properly decoded. The association of these structures with consciousness manipulation should not seem so surprising by now, for as I noted in
Genes, Giants, Monsters and Men
, piezoelectric effects are used in modern mind manipulation technologies,
9
and some ancient temples from classical times also appear to have been deliberately engineered to be in resonance with certain frequencies of the human brain.
10
It is, oddly enough, point 9)b)ii) above — the use of musical codes in the Platonic and Pythagorean traditions — rather than the quantum mechanical and astronomical encoding, that points directly to the next necessary stage in our speculative case that pyramidal structures are hyper-dimensional machines, designed to manipulate the medium itself, in all its effects, including consciousness.
In this respect, let us recall something stated in chapter nine:
It is important to note what this notation means, for cubing and squaring a number — e.g. x3 and x2 — are, of course,
geometrical
functions describing objects in two or three spatial dimensions
. Thus, the notation {2,5} mentioned above could be written this way more abstractly as {x, y}, and since the first number is multiplied by the cubic power of 60, and the second by the squared power of 60, the notation really would look like this:
We can therefore imagine
extending
this notation to {x,y,z}, and extending the powers of 60 with which each number is multiplied, e.g.in other words, notations such as {8,0,0}, which are also within the realm of possibility in ancient Mesopotamian notation, conceivably may be understood as representing powers of 60
greater
than the cubic, that is to say, as geometric and numerical representations of objects in
four
or more dimensions.
To state it as succinctly as possible, the very structure of ancient Mesopotamian numerical notation implies a basic familiarity with hyper-dimensional geometries and the basic mathematical techniques for describing objects in four or more spatial dimensions. Indeed, as we shall discover in chapter 13,
the exact same notation convention began to be used in nineteenth century geometrical techniques for describing objects in four or more dimensions!
This contains a further, and very suggestive, implication, for it is to be noted that the Sumerian-Babylonian gods may be described by such notation. In other words,
the gods were being described peculiar union of physics and religion, as hyper-dimensional entities or objects.
11
As I noted in that chapter in the footnote: “The modern name for such notations is Schl㥬i numbers, and their appearance in notation is identical, with each number representing a particular type of geometric function. This will be explored further in chapter 13.”
12
This is now chapter thirteen, and a closer look at those mysterious Babylonian notations, so curiously identical to modern Schläi
notations, is in order, for in them is contained a profound clue to some of the ancient pyramids,
particularly
the ones in Mexico and Meso-America.
B. Hints of a Hyper-Dimensional Engineering:
A Cursory Excursion into Geometry in More than Three Dimensions
It has been suggested in some circles that some of the pyramids of the ancient world, in particular those of Meso-America and Egypt, represent structures designed to engineer the hyper-dimensional physics of the medium. Richard C. Hoagland, for example, performed simple experiments on television recently, using a Bullova watch, powered by a minute tuning-fork, to take measurements of changes in the tuning fork’s frequency of vibration at various places near the pyramids of Tikal. When Mr. Hoagland moved away from the structures, the vibrations would return to normal, but near or on the structures, the vibrations varied greatly from their normal frequency, suggesting to him that that structures were manipulating local inertial effects. I myself have suggested that at least the Great Pyramid was a complex sort of phase conjugate howizter manipulating longitudinal waves in the physical medium itself.
But to argue that the pyramids of Mexico and Egypt
in general
are designed as hyper-dimensional machines —
analogues
of objects in higher-dimensional spaces — requires an additional type of analysis, and this can only be had by doing a bit of hyper-dimensional geometry. Unfortunately, presenting the mathematical techniques that geometers use to analyze such objects to a lay readership is no easy task, but inevitably,
some
degree of familiarity with these mathematical techniques is required, howsoever cursory.
Fortunately, we have already encountered, through the work of Carl Munck,
the
essential analytical conception used by geometers to describe hyper-dimensional objects, and that is
the simple technique of counting three things:
1) lines, or e d g e s ;
2) points, or corners, or, as the geometers call them, vertices; and,
3) sides, or faces.
For our purposes, we shall attempt to summarize crucial conceptions in hyper-dimensional geometry using what may justifiably be described as the single best mathematical treatment of the subject: mathematician H.S.M. Coxeter’s
Regular Polytopes.
1. Geometry in More than Three Dimensions:
H.S.M. Coxeter’s
Regular Polytopes
a. A Brief Biography

Harold Scott MacDonald Coxeter, 1907-2003
One of the twentieth century’s greatest mathematicians, Harold Scott MacDonald Coexeter, is virtually unknown outside of mathematics, for the speciality that earned him his fame — hyper- dimensional geometry or geometry in more than three spatial dimensions — requires, needless to say, a powerful pictorial imagination and the ability to put that imagination into formally explicit and reproducible equations. Coexter had both, in abundance. Like so many who dwell on that fuzzy boundary between mathematics and the arts, Coxeter was a talented musician, being an accomplished pianist by the age of ten.
13
Born in London in 1907, Coxeter attended the University of Cambridge, receiving his B.A. in the subject in 1928 and his P.D. in 1931. He spent a year at the Princeton University in 1932 as a Rockefeller Fellow, working with the famous mathematician and physicist Hermann Weyl. As the war clouds of World War Two were gathering, Coexter moved to the University of Toronto in 1936, eventually becoming a professor there in 1948. His hyper- dimensional geometry work inspired the famous Dutch artist Maurits Escher, whom Coxeter met.
14
Coxeter published but few books and papers during his long and distinguished career, but that is hardly surprising, for anyone who has read any of his books or papers knows that each of them is a higher- dimensional tour-de-force, whose very equations and diagrams are themselves exercises in alchemical transformations and expansions of conciousness, working an almost magical effect on the mind. Of these few publications,
Regular Polytopes
is his distilled masterpiece, a model of mathematical rigor and yet, an essay of profound beauty. It is this book, and in particular its all-important opening pages, that we shall follow closely here, for they contain profound clues to unravel the mystery of the pyramids,
particularly those that depart from the smooth- faced Egyptian model.