From Eternity to Here (40 page)

In Figure 54, we see the evolution of the entropy in a divided box of gas with 2,000 particles, but now at a later time, after it has reached equilibrium. Note that this is an extreme close-up on the change in entropy; whereas the plots in Chapter Eight showed the entropy evolving from about 0.75 up to 1, this plot shows the entropy ranging from between 0.997 and 1.

What we see are small fluctuations from the equilibrium value where the entropy is maximal and the molecules are equally divided. This makes perfect sense, the way we’ve set up the situation; most of the time, there will be equal numbers of particles on the right side of the box and the left side, but occasionally there will be a slight excess on one side or the other, corresponding to a slightly lower entropy. It’s exactly the same idea as flipping a coin—on average, a sequence of many coin flips will average to half heads and half tails, but if we wait long enough, we will see sequences of the same result many times in a row.

The fluctuations seen here are very small, but on the other hand we didn’t wait very long. If we stretched out the plot to much longer times—and here we’re talking
much
longer times—the entropy would eventually dip down to its original value, representing a state with 80 percent of the particles on one side and only 20 percent on the other. Keep in mind that this graph shows what happens with 2,000 particles; in the real world, with many more particles in any macroscopic object, fluctuations in entropy are correspondingly smaller and more rare. But they will be there; that’s an inevitable consequence of the probabilistic nature of entropy.

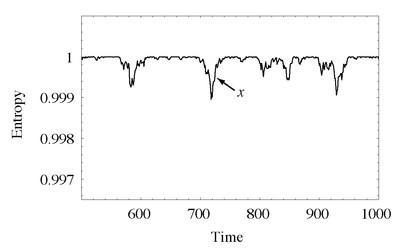
Figure 54:
The evolution of the entropy of a divided box of gas, starting from equilibrium. The state spends most of its time near maximum entropy, but there are occasional fluctuations to lower-entropy states. Note from the vertical axis that we have zoomed up close; typical fluctuations are very small. The point
x
marks a return to equilibrium from a relatively large fluctuation.

So here is Boltzmann’s final, dramatic suggestion: Maybe the universe is like that. Maybe time does last forever, and the underlying laws of physics are Newtonian and reversible, and maybe the assumptions underlying the recurrence theorem are valid.
¹⁸⁰
And maybe, therefore, the plot of entropy versus time shown in Figure 54 is how the entropy of the real universe actually evolves.

THE ANTHROPIC APPEAL

But—you say—that can’t be right. On that graph, entropy goes up half the time and goes down half the time. That’s not at all like the real world, where entropy only ever goes up, as far as we can see.

Ah, replies Boltzmann, you have to take a wider view. What we’ve shown in the plot are tiny fluctuations in entropy over a relatively short period of time. When we’re talking about the universe, we are obviously imagining a huge fluctuation in entropy that is very rare and takes an extremely long time to play itself out. The overall graph of the entropy of the universe looks something like Figure 54, but the entropy of our local, observable part of universe corresponds to only a very tiny piece of that graph—near the point marked
x
, where a fluctuation has occurred and is in the process of bouncing back to equilibrium. If the entire history of the known universe were to fit there, we would indeed see the Second Law at work over our lifetimes, while over ultra-long times the entropy is simply fluctuating near its maximum value.

But—you say again, not quite ready to give up—why should we live at that particular part of the curve, in the aftermath of a giant entropy fluctuation? We’ve already admitted that such fluctuations are exceedingly rare. Shouldn’t we find ourselves at a more typical period in the history of the universe, where things basically look like they are in equilibrium?

Boltzmann, naturally, has foreseen your objection. And at this point he makes a startlingly modern move—he invokes the
anthropic principle
. The anthropic principle is basically the idea that any sensible account of the universe around us must take into consideration the fact that we exist. It comes in various forms, from the uselessly weak—“the fact that life exists tell us that the laws of physics must be compatible with the existence of life”—to the ridiculously strong—“the laws of physics had to take the form they do because the existence of life is somehow a necessary feature.” Arguments over the status of the anthropic principle—Is it useful? Is it science?—grow quite heated and are rarely very enlightening.

Fortunately, we (and Boltzmann) need only a judicious medium-strength version of the anthropic principle. Namely, imagine that the real universe is much bigger (in space, or in time, or both) than the part we directly observe. And imagine further that different parts of this bigger universe exist in very different conditions. Perhaps the density of matter is different, or even something as dramatic as different local laws of physics. We can label each distinct region a “universe,” and the whole collection is the “multiverse.” The different universes within the multiverse may or may not be physically connected; for our present purposes it doesn’t matter. Finally, imagine that some of these different regions are hospitable to the existence of life, and some are not. (That part is inevitably a bit fuzzy, given how little we know about “life” in a wider context.) Then—and this part is pretty much unimpeachable—we will always find ourselves existing in one of the parts of the universe where life is allowed to exist, and not in the other parts. That sounds completely empty, but it’s not. It represents a
selection effect
that distorts our view of the universe as a whole—we don’t see the entire thing; we see only one of the parts, and that part might not be representative.

Boltzmann appeals to exactly this logic. He asks us to imagine a universe consisting of some collection of particles moving through an absolute Newtonian spacetime that exists for all eternity. What would happen?

There must then be in the universe, which is in thermal equilibrium as a whole and therefore dead, here and there relatively small regions of the size of our galaxy (which we call worlds), which during the relatively short time of eons deviate significantly from thermal equilibrium. Among these worlds the state probability [entropy] increases as often as it decreases. For the universe as a whole the two directions of time are indistinguishable, just as in space there is no up or down. However, just as at a certain place on the earth’s surface we can call “down” the direction toward the centre of the earth, so a living being that finds itself in such a world at a certain period of time can define the time direction as going from less probable to more probable states (the former will be the “past” and the latter the “future”) and by virtue of this definition he will find that this small region, isolated from the rest of the universe, is “initially” always in an improbable state.
¹⁸¹

This is a remarkable paragraph, which would be right at home in a modern cosmology discussion, with just a few alterations in vocabulary. Boltzmann imagines that the universe (or the multiverse, if you prefer) is basically an infinitely big box of gas. Most of the time the gas is distributed uniformly through space, at constant temperature—thermal equilibrium. The thing is, we can’t live in thermal equilibrium—it’s “dead,” as he bluntly puts it. From time to time there will be random fluctuations, and eventually one of these will create something like the universe we see around us. (He refers to “our galaxy,” which at the time was synonymous with “the observable universe.”) It’s in those environments, the random fluctuations away from equilibrium, where we can possibly live, so it’s not much surprise that we find ourselves there.

Even in the course of a fluctuation, of course, the entropy is only increasing half the time—in the other half it’s decreasing, moving from equilibrium down to the minimum value it will temporarily reach. But this sense of “increasing” or “decreasing” describes the evolution of entropy with respect to some arbitrarily chosen time coordinate, which—as we discussed in the last chapter—is completely unobservable. As Boltzmann correctly points out, what matters is that the current universe is in the middle of a transition from a low-entropy state to one of thermal equilibrium. In the midst of such a transition, any living beings who pop up will always label the direction of lower entropy “the past,” and the direction of higher entropy “the future.”

Figure 55:
Boltzmann’s “multiverse.” Space is mostly a collection of particles in equilibrium, but there are occasional local fluctuations to low-entropy states. (Not at all to scale.) We live in the aftermath of one exceptionally large fluctuation.

This is a provocative picture of the universe. On large scales, matter is almost always in a dilute collection of gas at some temperature. But every so often, over the course of billions of years, a series of random accidents conspire to create pockets of anomalously low entropy, which then relax back to equilibrium. You, and I, and all the bustling activity we see around us, are epiphenomena riding the wave of entropy as it bounces back from a random excursion into a wildly improbable state.
¹⁸²

So what does a typical downward fluctuation in entropy look like? The answer, of course, is that it looks exactly like the time-reverse of a typical evolution from a low-entropy state back to a high-entropy one. The whole universe wouldn’t suddenly zoom from a thin gas of particles into a dense Big-Bang-like state in a matter of minutes; it would, most of the time, experience a series of unlikely accidents spread over billions of years, all of which would decrease the entropy just a little bit. Stars and galaxies would un-form, omelets would turn into eggs, objects in equilibrium would spontaneously develop substantial temperature gradients. All of these would be completely independent events, each individually unlikely, and the combination of all of them is fantastically unlikely. But if you truly have eternity to wait, even the most unlikely things will eventually happen.

SWERVING THROUGH ANTIQUITY

Boltzmann wasn’t actually the first to think along these lines, if we allow ourselves a little poetic license. Just as Boltzmann was concerned with understanding the world in terms of atoms, so were his predecessors in ancient Greece and Rome. Democritus (c. 400 B.C.E.) was the most famous atomist, but his teacher Leucippus was probably the first to propose the idea. They were materialists, who hoped to explain the world in terms of objects obeying rules, rather than being driven by an underlying “purpose.” In particular, they were interested in rising to the challenge raised by Parmenides, who argued that change was an illusion. The theory of unchanging atoms moving through a void was meant to account for the possibility of motion without imagining that something arises from nothing.

One challenge that the atomists of antiquity faced was to explain the messy complexity of the world around them. The basic tendency of atoms, they believed, was to fall downward in straight lines; that doesn’t make for a very interesting universe. It was left to the Greek thinker Epicurus (c. 300 B.C.E.) to propose a solution to this puzzle, in the form of an idea called “the swerve” (
clinamen
).
¹⁸³
Essentially Epicurus suggested that, in addition to the basic tendency of atoms to move along straight lines, there is a random component to their motion that occasionally kicks them from side to side. It’s vaguely reminiscent of modern quantum mechanics, although we shouldn’t get carried away. (Epicurus didn’t know anything about blackbody radiation, atomic spectra, the photoelectric effect, or any of the other experimental results motivating quantum mechanics.) Part of Epicurus’s reason for introducing the swerve was to leave room for free will—basically, to escape the implications of Laplace’s Demon, long before that mischievous beast had ever reared his ugly head. But another motivation was to explain how individual atoms could come together to form macroscopic objects, rather than just falling straight down to Earth.