Birth of a Theorem: A Mathematical Adventure (34 page)

Read Birth of a Theorem: A Mathematical Adventure Online

Authors: Cédric Villani

Tags: #Non-Fiction, #Science, #Biography

BOOK: Birth of a Theorem: A Mathematical Adventure

3.98Mb size Format: txt, pdf, ePub

Therefore, as an effect of the singularity of the interaction,
we expect to lose a fractional exponential on the convergence rate
: if the mode
k
of the source decays like
then
ϕ
_k, the mode
k
of the solution, should decay like
More generally, if the mode
k
decays like
A
(
kt
), one expects that
φ
_k(
t
) decays like
Then we conclude as before by absorbing the fractional exponential in a very slow exponential, at the price of a
very large
constant: say,

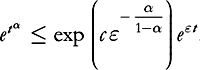
[From my 2010 Luminy Summer School lecture notes on Landau damping]

THIRTY-SEVEN

Charlotte

November 1, 2009

In transit between Palm Beach and Providence. An impersonal airport in North Carolina; it could be anywhere, really. Removing all metal items when you pass through the security checkpoint is a bit of a chore for most people, but when you also wear cuff links and a fob watch, and on top of that carry one or two USB flash drives and a half dozen pens in your pockets …

In Florida, at the international workshop on geometric inequalities that Emanuel Milman helped organize in Boca Raton, the living was easy! From downtown it was only a few steps to the beach. And the ocean was like a warm bath. Even at night the temperature was ideal, no one around, no need for a bathing suit … really, it was like swimming in a bathtub—a bathtub with tides and soft sand! And all this in November!

But now the fun’s over, back to the cold. It’s going to happen so fast, thanks to the unnatural swiftness of modern air travel!

In Boca Raton I was able to forget Landau damping for a day or two, but now once again it occupies my every waking moment. I’m beginning to see what needs to be done to make the proof stronger overall, how to exploit the flash of inspiration that struck me in Ann Arbor. Still, it’s going to be a huge amount of work! Waiting for the connecting flight to Providence, I wasn’t sure if I really had enough confidence to talk about the new plan of attack at Brown without having yet worked out all the details. It’s a very important talk: Yan Guo, the one by whom the Problem came, is going to be in the audience.

I took out a blank piece of paper and began to sketch the new plan, redoing calculations etc., when all of a sudden it leapt to my eyes—there’s something wrong, a contradiction.

I can’t possibly prove an estimate that sharp.…

After a few minutes I’d convinced myself that there must be a mistake somewhere in one of the especially involved parts of the proof. Or could it be that—it’s
all
wrong? The airport began to pitch and roll around me.…

I pulled myself together.

Cédric, the error can’t be very serious. Everything else holds together too well. The error has to be local, it’s got to be right here, in this passage somewhere. The reason for it has to be that the calculation is obscured by these two miserable little shifts—the double time-shift you introduced after coming back from the museum!

But Clément definitely showed that we can do without them!! So be it, we’ll have to get rid of them after all, they’re too dangerous. In a proof this complex, the least source of obscurity must be ruthlessly eliminated.

Even so, if I hadn’t come up with this double shift we might have been stymied for good. The double shift was the thing that gave us hope, that allowed us to move forward again. Later on, we saw that it wasn’t necessary. And so what if in the end it turns out to be wrong!? Fine. We’ll rewrite everything, without even mentioning it.

For the moment I need to decide what to say tomorrow at Brown. I’ll have to say that I’ve found a way to improve the proof, and then explain why it’s important, because it will answer the two criticisms of our result that have been made over and over again. But I mustn’t cheat—no bluffing this time!

Palm Beach to Providence, more turbulence than expected …

* * *

SUMMARY OF YOUR WEST PALM BEACH–PROVIDENCE TRIP

Flight details:
Sunday 1 November 2009

Travel time: 6 hrs 39 mins

Depart:
03:00 PM, West Palm Beach, FL (PBI)

Arrive:
04:53 PM, Charlotte, NC (CLT)

US Airways 1476 Boeing 737-400 Economy Class

Depart:
07:49 PM, Charlotte, NC (CLT)

Arrive:
09:39 PM, Providence, RI (PVD)

US Airways 828 Airbus A319 Economy Class

* * *

Coulomb/Newton (most interesting case)

Coulomb/Newton interaction and analytic regularity are
both
critical in the proof of nonlinear Landau damping; but the proof still works for
exponentially large times
“because”

• the expected linear decay is exponential

• the expected nonlinear growth is exponential

• the Newton scheme converges bi-exponentially

Still, it seems possible to go further by exploiting the fact that
echoes at different spatial frequencies are asymptotically rather well separated.

[From notes for my talk at Brown University, November 2, 2009]

THIRTY-EIGHT

Saint-Rémy-lès-Cheuvreuse

November 29, 2009

Sunday morning, scribbling away in bed. One of the special moments in the life of a mathematician.

I’m rereading the final version of our article, crossing out, correcting. More relaxed than I’ve been in months! We’ve rewritten the whole thing. Completely eliminated the treacherous double shift. Succeeded in exploiting the asymptotic time separation of the echoes, recast the main part of the proof, substituted a mode-by-mode study for the original aggregate-level treatment, relaxed the analyticity condition, and, last but not least, included the Coulomb case in infinite time, the thing that everyone had been complaining about for so long.… Everything revised, everything simplified, everything checked once more, everything improved, everything gone over one last time.

All of this could easily have taken three months, but in our present state of feverish excitement three weeks turned out to be enough.

More than once, going through the argument with a fine-toothed comb, we’ve wondered how in the world we could have come up with this little trick or that little piece of cleverness.

The result is now much stronger. In the process we also managed to solve a problem that has long intrigued specialists such as Guo, technically known as the orbital stability of homogeneous nonmonotonic linearly stable equilibria.

We added a few passages, but simplifying has reduced the length elsewhere, so that now the manuscript is scarcely longer than the one we submitted earlier.

New computer simulations came in as well. When I saw the first batch of results last week, I was staggered: the numerical calculations that Francis had performed using an extremely precise formula seemed to completely contradict our theoretical results! But I didn’t buckle. I told Francis I was skeptical, and he reran everything using another method that is considered to be even more accurate. When the second batch came in, the results were consistent with the theoretical prediction. Phew! Just goes to show that computer simulations are no substitute for qualitative insight.

Tomorrow we’ll be ready to make the new version available via the Internet. And at the end of the week we’ll be able to resubmit the paper to
Acta Mathematica
,
with a much greater chance of success this time around.

In my idle moments I can’t help but think of Poincaré himself. One of his most famous articles was, well, not rejected by
Acta
,
but nevertheless withdrawn, and then corrected and finally republished. Perhaps the same thing is going to happen to me? It’s already been my Poincaré year: I won the Henri Poincaré Prize, and I’m head of the Institut Henri Poincaré.

Poincaré … careful, Cédric, beware delusions of grandeur!

* * *