Birth of a Theorem: A Mathematical Adventure (41 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

Assume that W and f
0
satisfy the generalized Penrose linear stability condition: for all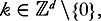 if we assume further that
if we assume further that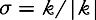 and for all
and for all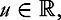
 then for all
then for all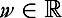 such that
such that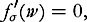 we have
we have
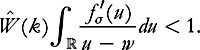
Now assume an initial position and velocity profile, f
i
(
x
,
v
)
≥
0
, very close to the analytic state f
0
, in the sense that its Fourier transform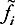 with respect to position and velocity satisfies
with respect to position and velocity satisfies
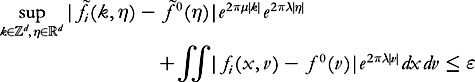
with
λ,
μ
>
0
, and
ε
>
0
small enough.
Then there exist analytic profiles f
+∞
(
v
), f
−∞
(
v
)
such that the solution of the nonlinear Vlasov equation, with interaction potential W and initial datum f
i
at time t
=
0
, satisfies
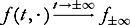
weakly; more precisely, in the sense of a pointwise, exponentially fast convergence of Fourier modes.
The convergence rate of the nonlinear equation is arbitrarily close to the convergence rate of the linearized equation, so long as
ε
>
0
is sufficiently small. Additionally, the marginals
∫
f dv and
∫
f dx converge exponentially fast to their equilibrium value, in all C
r
spaces.
All the estimates appearing in the nonlinear statement are constructive.

Clément Mouhot

