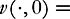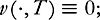Birth of a Theorem: A Mathematical Adventure (15 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography


Luc Tartar
“Really? Well, maybe, I don’t know. In any case I did that in order to construct impossible solutions to certain elliptical equations. And then I realized that there was a general formula.”
He explained the formula.
“Yes, of course, that’s Gromov’s method of convex integration!”
“Really? No, I don’t think so. What I was doing is much simpler. The construction is very straightforward, it works because you’re in the convex envelope and you can express the approximate solution each time as a convex combination, and then.…”
But these are the main elements of convex integration theory! Did this guy really rediscover everything all by himself, without any idea what other people had already done? Where was he living? On Mars?
“So what about fluid mechanics?”
“Oh, right! I’d heard Mandelbrot give a talk, and I said to myself, I’d like to do something similar. So I began to study Euler’s equations from the fractal point of view, and I realized that I could reinterpret the same kind of things I’d done in my thesis. But it was complicated.”
I was on the edge of my seat, listening intently. Then, after making two or three general remarks, he abruptly stopped.
“I’m sorry, I’ve got to go now. I use public transportation, just now with the snow it’s very slippery and my balance isn’t very good, it’s a rather long walk home from the bus stop, and…”
Once he’d finally gone through all the reasons why he had to leave right away, the monologue came to an end. The time we’d actually spent discussing mathematics was no more than five minutes, from which I learned nothing. To think that this was the same man who is responsible for the most amazing theorem in all of fluid mechanics! Living proof that having a superior mind is no guarantee of being able to communicate.
I returned to Joel’s office and told him about my meeting with Scheffer. I said that I was sorry it had been so brief.
“Cédric, five minutes with Vlad is about as much time as anyone in the department has spent talking with him in the last five years.”
An experience that will remain forever engraved in my memory.… But now it was time to go back to thinking about Landau damping.
On the way home, my doubts returned once more.
Finally I realized the proof isn’t going to work.
The talk at Rutgers marked a turning point in my quest. To announce results you have not yet proved is a grave sin, a violation of the bond of trust that unites a speaker and his audience. My back was to the wall: if I was ever to make up for my transgression, I had to prove the result I had just announced.
John Nash, my mathematical hero, is said to have regularly put himself under fantastic pressure by announcing results that he did not yet know how to prove. There is no question he did this at least once, in the case of the isometric embedding theorem.
On my way home that day I began to feel something like the pressure Nash must have felt. The terrible sense of urgency that now hung over me was not going to go away until I succeeded, one way or another, in completing this proof. I
had
to complete it—or else forever be disgraced!!
* * *
Imagine you’re walking through the woods on a peaceful summer’s afternoon. You pause at the edge of a pond. Everything is perfectly calm, not the slightest breeze.
Suddenly the surface of the pond becomes agitated, as though seized by convulsions; a few moments later, it is sucked down into a roaring whirlpool.
And then, a few moments after that, everything is calm once more. Still not a breath of air, not even a ripple on the surface from a fish swimming beneath it. So what happened?
The Scheffer–Shnirelman paradox, surely the most astonishing result in all of fluid mechanics, proves that such a monstrosity is possible, at least in the mathematical world.
It is not based on an exotic model of quantum probabilities or dark energy or anything of that sort. It rests on the incompressible Euler equations, the oldest of all partial differential equations, used by mathematicians and physicists everywhere to describe a perfectly incompressible fluid without any internal friction.
It has been more than two hundred fifty years since Euler derived his fundamental equations, and yet not all of their mysteries have been penetrated. Indeed, they are still considered to mark out one of the most treacherous regions of the mathematical world. When the Clay Mathematics Institute set seven “millennium problems” in 2000, offering $1 million apiece for their solution, it did not hesitate to include the regularity of solutions to the Navier–Stokes equations. It was very careful, however, to avoid any mention of Euler’s equations—a far greater and more terrifying beast.
And yet at first glance Euler’s equations seem so simple, so innocent, utterly devoid of guile or cunning. No need to model variations in density or to grapple with the enigmas of viscosity. One has only to write down the classical laws of conservation: conservation of mass, quantity of motion, and energy.
But then … suddenly, in 1993, Scheffer showed that Euler’s equations in the plane are consistent with the spontaneous creation of energy! Energy created from nothing! No one has ever seen such bizarre behavior in fluids in the natural world! All the more reason, then, to suspect that Euler’s equations hold still more surprises in store for us. Big surprises.
Scheffer’s proof is a stunning feat of mathematical virtuosity, as obscure as it is difficult. I doubt that anyone other than its author has read it carefully from beginning to end, and I am certain that no one could reconstruct its reasoning, unaided, in every detail.
There was more to come. Four years later, in 1997, the Russian-born mathematician Alexander Shnirelman, renowned for his originality, presented a new proof of this staggering result. Shortly afterward Shnirelman proposed a physically realistic criterion for solutions to Euler’s equations that would prohibit pathological phenomena of the sort Scheffer had discovered.
Alas! A few years ago, two brilliant young mathematicians, Camillo De Lellis, an Italian, and László Székelyhidi, a Hungarian, proved a general and still more shocking theorem that showed, among other things, that Shnirelman’s criterion was powerless to resolve the paradox. Additionally, using the techniques of convex integration, they were able to develop a new method for producing these “wild” solutions, an elegant procedure that grew out of earlier research by a number of mathematicians, including Vladimir
Š
verák, Stefan Müller, and Bernd Kirchheim. Thanks to De Lellis and Székelyhidi, we now realize that even less is known about Euler’s equations than we thought.
And what we thought we knew wasn’t much to begin with.
* * *
Excerpt from the 2008 Bourbaki Seminar Talk
Theorem [Scheffer (1993), Shnirelman (1997)].
There exists a nonzero weak solution of the incompressible Euler equations in dimension 2,
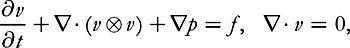
without forcing (
f
≡
0), with compact support in space-time.
Theorem [De Lellis and Székelyhidi (2007, 2008)].
Let
Ω
be an open interval of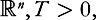 and
and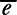 a uniformly continuous function
a uniformly continuous function
Ω
×
]0,
T
[
→
]0,
+∞
[, with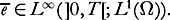 Then for all
Then for all
η
>
0 there exists a weak solution (
v
,
p
) of the Euler equations, without forcing (
f
≡
0), such that
(i)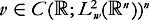 ;
;
(ii)
v
(
x
,
t
)
=
0 if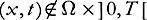 ; in particular
; in particular