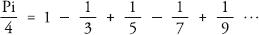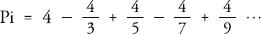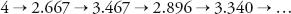Alex’s Adventures in Numberland (25 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

This translates into 3.14084 < pi < 3.14289, an accuracy of two decimal places.
But pi hunters weren’t about to stop there. In order to get closer to the number’s true value, all that was required was to create polygons with more sides. Liu Hui, in third-century China, employed a similar method, using the area of a polygon of 3072 sides to pin pi to five decimal places: 3.14159. Two centuries later Tsu ChungChih and his son Tsu Keng-Chih went one digit further, to 3.141592, with a polygon of 12,288 sides.
The Greeks and the Chinese were hampered by cumbersome notation. When mathematicians were eventually able to use Arabic numerals, the record tumbled. In 1596 the Dutch fencing master Ludolph van Ceulen used a souped-up polygon of 60 × 2
29
sides to find pi to 20 decimal places. The pamphlet on which he printed his result ended with the words: ‘whoever wants to, can come closer’, and no one felt the urge as strongly as he did. He went on to calculate pi to 32 and then 35 decimal places – which were engraved on his tombstone. In Germany,
die Ludolphsche Zahl
, Ludolph’s number, is still understood as a term for pi.
For 2000 years the only way to pinpoint pi with accuracy was by using polygons. But, in the seventeenth century, Gottfried Leibniz and John Gregory ushered in a new age of pi appreciation with the formula:
In other words, a quarter of pi is equal to one minus a third plus a fifth minus a seventh plus a ninth and so on, alternating the addition and subtraction of unit fractions of the odd numbers as they head to infinity. Before this point scientists were only aware of the scatter-gun randomness of pi’s decimal expansion. Yet here was one of the most elegant and uncomplicated equations in maths. Pi, the poster boy of disorder, it turned out, had some kind of order in his DNA.
Leibniz had devised the formula using ‘the calculus’, a powerful type of mathematics he had discovered, in which a new understanding of infinitesimal amounts was used to calculate areas, curves and gradients. Isaac Newton had also come up with calculus, independently, and the men spent a good deal of time bickering about who had got there first. (For years, Newton was considered to have won the argument, based on the dates of his unpublished manuscripts, but it now appears that a version of calculus was actually first invented in the fourteenth century by the Indian mathematician Madhava.)
The formula that Leibniz found for pi is what is known as an
infinite series
, a sum that goes on and on for ever, and it provides a way to calculate pi. First, we need to multiply both sides of the formula by 4 to get:
Starting with the first term and adding successive terms produces the following progression (converted into decimals):
The total gets closer and closer to pi in smaller and smaller leaps. Yet this method requires more than 300 terms to get an answer for pi accurate to two decimal places, so it was impracticable for those wanting to use it to find more digits in the decimal expansion.
Eventually, calculus provided other infinite series for pi that were less pretty but more effective for number-crunching. In 1705 the astronomer Abraham Sharp used one to calculate pi to 72 decimal places, smashing van Ceulen’s century-old record of 35. While this was quite an achievement, it was also a useless one. There is no practical reason to know pi to 72 digits, or to 35 digits for that matter. Four decimal places is enough for the engineers of precision instruments. Ten decimal places is sufficient to calculate the circumference of the Earth to within a fraction of a centimetre. With 39 decimal places, it is possible to compute the circumference of a circle surrounding the known universe to within an accuracy of a radius of a hydrogen atom. But practicality wasn’t the point. Application was not a concern to the pi men of the Enlightenment; digit-hunting was an end in itself, a romantic challenge. A year after Sharp’s effort, John Machin reached 100 digits and in 1717 the Frenchman Thomas de Lagny added a further 27. By the turn of the century, the Slovenian Jurij Vega was in the lead with 140.
Zacharias Dase, the German lightning calculator, pushed the record for pi to 200 decimal places in 1844 in an intense two-month burst. Dase used the following series, which looks more convoluted than the pi formula above but is in fact far more user-friendly. This is because, first, it bears down on pi at a respectable rate. An accuracy of two decimal places is reached after the first nine terms. Second, the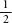 ,
,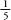 and
and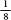 that reappear every third term are very convenient to manipulate. If
that reappear every third term are very convenient to manipulate. If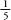 is rewritten as
is rewritten as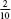 and
and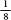 as
as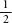 ×
×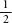 ×
×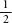 , all the multiplications involving those terms can be reduced to combinations of doubling and halving. Dase would have written out a reference table of doubles to help him with his calculations, starting 2, 4, 8, 16, 32, and carried on for as far as he needed – which, since he was calculating pi to 200 places, would be when the final double is 200 digits long. This happens after 667 successive doublings.
, all the multiplications involving those terms can be reduced to combinations of doubling and halving. Dase would have written out a reference table of doubles to help him with his calculations, starting 2, 4, 8, 16, 32, and carried on for as far as he needed – which, since he was calculating pi to 200 places, would be when the final double is 200 digits long. This happens after 667 successive doublings.