Alex’s Adventures in Numberland (11 page)
Read Alex’s Adventures in Numberland Online
Authors: Alex Bellos

Place-value counting systems have been used all over the world. Instead of pebbles in furrows, the Incas used beans or grains of maize in trays. North American Indians threaded pearls or shells on different-coloured string. The Greeks and Romans used counters of bone, ivory or metal on tables that had different columns marked out. In India they used marks on sand.
The Romans also made a mechanical version, with beads sliding in slots, called an abacus. These portable versions spread through the civilized world, though different countries preferred different versions. The Russian
schoty
has ten beads per rod (except on the row that has four beads, used by cashiers to denote quarter roubles). The Chinese
suan-pan
has seven, while the Japanese
soroban
, like the Roman abacus, has just five.
About a million children annually in Japan learn the abacus, attending one of 20,000 after-school abacus clubs. One evening in Tokyo I visited one in a west Tokyo suburb. The club was a short walk from a local train line, on the corner of a residential block. Thirty brightly coloured bicycles were parked outside. A large window displayed trophies, abacuses and a line of wooden slats with the calligraphied names of its star pupils.

The Japanese equivalent of ‘reading, ’riting and ’rithmetic’ is
yomi, kaki, soroban
, or reading, writing, abacus. The phrase dates from the period in Japanese history between the seventeenth and nineteenth centuries when the country was almost totally isolated from the rest of the world. As a new merchant class emerged, which required skills other than proficiency with a samurai sword, so did a culture of private community-run schools that taught language and arithmetic – with the focus on abacus training.
Yuji Miyamoto’s abacus club is a modern descendant of these older
soroban
establishments. When I walked in, Miyamoto, who was wearing a dark blue suit and white shirt, was standing in front of a small classroom of five girls and nine boys. He was reading out numbers in Japanese with the breathless syncopation of a horseracing commentator. As the children added them all up, the clatter of beads sounded like a swarm of cicadas.
In a
soroban
, there are exactly ten positions of beads per column, representing the numbers from 0 to 9, as shown overleaf.
When a number is displayed on the
soroban
, each digit of the number is represented on a separate column using one of the ten positions.
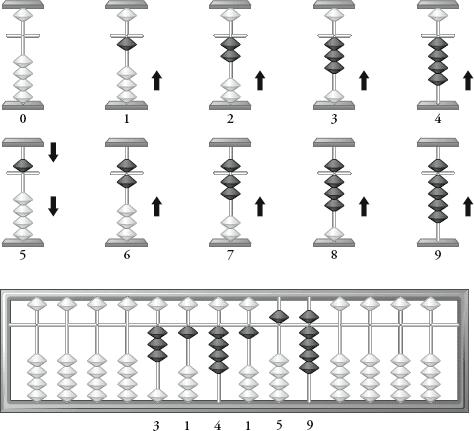
Numbers on the soroban.
The abacus was invented as a way of counting, but it really came into its own as a method for calculation. Arithmetic became much easier to do when helped by the flicking of beads. For example, to calculate 3 plus 1 you start with 3 beads, move 1 bead and the answer is right before your eyes – 4 beads. To calculate, say, 31 plus 45 you start with two columns marking 3 and 1, move 4 bead positions up the left column and 5 up the right column. The columns now read 7 and 6, which is the answer, 76. With a little bit of practice and application, it becomes easy to add numbers of any length so long as there are enough coumns to accommodate them. If on any one column the two numbers add up to more than ten, then you will need to move the beads on the column to the left up one position. For example, 9 plus 2 on one column moves to a 1 on the column to the left and a 1 on the original column, expressing the answer, 11. Subtraction, multiplication and division are a little more complicated, but once mastered can be done extremely quickly.
Until the availability of cheap calculators in the 1980s abacuses were commonly seen on shop counters from Moscow to Tokyo. In fact, during the transition between the manual and electronic eras, a product combining both calculator and abacus was sold in Japan. Addition is usually faster on the abacus since you get your answer as soon as you input the numbers. With multiplication the electronic calculator gives you a slight speed advantage. (The abacus was also a way for the sceptical abacist to check the calculator’s result, just in case he didn’t believe it.)

Sharp’s abacus-calculator.
Abacus use has dropped in Japan since the 1970s when, at its peak, 3.2 million pupils a year sat the national
soroban
proficiency exam. Yet the abacus still remains a defining aspect of growing up, a mainstream extra-curricular activity like swimming, violin or judo. Abacus training, in fact, is run like a martial art. Levels of ability are measured in dans, and there is a competitive structure of local, provincial and national competitions. One Sunday I went to see a regional event. Almost 300 children, aged between 5 and 12, sat at desks in a conference hall with an array of special
soroban
accessories, like sleek abacus bags. An announcer stood at the front of the hall and dictated, with the intonation of an impatient muezzin, numbers to be added, subtracted or multiplied. It was a knock-out competition that lasted several hours. A chorus of military brass-band music was pumped through the sound system when the trophies – each with a winged figure holding an abacus aloft – were presented to the victors.
At Miyamoto’s school he introduced me to one of his best pupils. Naoki Furuyama, aged 19, is a former national
soroban
champion. He was dressed casually, with a light checked shirt over a black T-shirt, and seemed a relaxed and well-adjusted teenager – certainly not the cliché of a socially awkward übergeek. Furuyama can multiply two six-digit numbers together in about four seconds, which is about as long as it takes to say the problem. I asked him what the point was of being able to calculate so fast, since there is no need for such skills in daily life. He replied that it helped his powers of concentration and self-discipline. Miyamoto was standing with us, and he interrupted. What was the point of running 26 miles, he asked me? There was never any need to run 26 miles, but people did it as a way of pushing human performance to the limit. Likewise, he added, there was a nobility in training one’s arithmetical brain as far as one could.
Some parents send their children to abacus club because it is a way to improve school maths results. But that does not completely explain the abacus’s popularity. Other after-school clubs provide more targeted maths tuition – Kumon, for example, a method of ploughing through worksheets that started in Osaka in the early 1950s, is now followed by more than four million children around the world. Abacus club is fun. I saw that in the faces of the pupils at Miyamoto’s school. They clearly enjoyed their dexterity at flicking the beads with speed and precision. The Japanese hetage of the
soroban
generates national pride. Yet the real joy of the abacus, I thought, is more primal: it has been used for thousands of years and, in some cases, is still the fastest way to do sums.
After a few years of using an abacus, when you are so familiar with the positioning of the beads, it becomes possible to perform calculations simply by visualizing an abacus in your head. This is called
anzan
, and Miyamoto’s top pupils have all learned it. The feat was amazing to watch – even though there was nothing to see. Miyamoto read out numbers to a totally silent, still classroom and within seconds the students raised their hands with the answers. Naoki Furuyama told me that he visualizes an abacus with eight columns. In other words, his imaginary abacus can display every number from 0 to 99,999,999.
Miyamoto’s abacus club is one of the best in the country in terms of the dans of its pupils and their achievements in national tournaments. Its speciality, however, is
anzan
. A few years ago Miyamoto decided to devise a type of arithmetical challenge that could only be answered using
anzan
. When you read out a sum to a pupil, for example, it can be answered in many different ways: using a calculator, pencil and paper, an abacus or
anzan
. Miyamoto wanted to show that there were some circumstances when
anzan
was the only possible method.
His solution was the computer game
Flash Anzan
, which he demonstrated for me. He told the class to get ready, pressed play and the pupils stared at a TV screen at the front of the room. The machine beeped three times to indicate it was about to start, and then the following 15 numbers appeared, one at a time. Each number appeared for only 0.2 seconds, so the whole thing was over in three seconds:
164
597
320
872
913
450
568
370
619
482
749
123
310
809
561
The numbers flashed by so quickly I barely had time to register them. Yet as soon as the last number flashed, Naoki Furuyama smiled and said the sum of the numbers was 7907.
It is impossible to solve a
Flash Anzan
challenge with a calculator or an abacus since there is no time to remember the digits being flashed at you, let alone type them into a machine or arrange beads.
Anzan
does not require you to remember the digits. All you do is shift the beads in your brain whenever you see a new number. You start with 0, then on seeing 164 instantly visualize the abacus on 164. On seeing 597 the internal abacus rearranges to the sum, which is 761. After 15 additions you cannot remember any of the flashed numbers nor the intermediate sums, but the imaginary abacus in your head will show the answer: 7907.
The wow factor of
Flash Anzan
has made it a national fad, and Nintendo has even released a
Flash Anzan
game for its DS consoles. Miyamoto showed me some clips from a
Flash Anzan
TV game show in which teenage
anzan
stars battled it out in front of screaming fans. Miyamoto says his game has helped recruit many new pupils to abacus clubs all over Japan. ‘People didn’t realize what you could do with
soroban
skills,’ he said. ‘With all this coverage, now they do.’
Neural imaging scans show that the parts of the brain activated by the abacus, or
anzan
, are different from the parts activated by normal arithmetical calculations and language. Traditional ‘pen and paper’ arithmetic depends on neural networks associated with linguistic processing. The
soroban
relies on networks associated with visuospatial information. Miyamoto simplifies this as ‘
soroban
uses the right brain, normal maths uses the left brain’. Not enough scientific research has been done to understand what benefits this segregation brings, or how it relates to general intelligence, concentration or other skills. Yet it does explain an astonishing phenomenon: that
soroban
experts are able to multitask in the most incredible way.
